Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Пермский национальный исследовательский политехнический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

1235.pdf

Скачиваний:

Добавлен:

15.11.2022

Размер:

12.71 Mб

Скачать

☆

<<< < Предыдущая 2 3 4 5 6 7 8 9 10 11 12 1314 / 4514 15 16 17 18 19 20 21 22 23 24 25 26 > Следующая >>>

Имеем
ф (2) =	sin За —3 sin 2 =
		З Г +	5!	■**		3 \		3!	+	51
						З3 —3		23 -	36- 3
						3!		23 -		5!
где						3!				5!
где		З3 —3	,	З3 —3
	ф1(2) =	З3 —3	,	З3 —3	г8- . . . .			Ф1.(0) = - 4 = * 0 ;
	ф1(2) =	3!		5!	г8- . . . .			Ф1.(0) = - 4 = * 0 ;
		3!		5!
ч (z) =	(sinг - г ) sinг = ( - J			J		-	...)	(	г	+. . . ) =*
где		=	г4( — 3! +			бГ —				— ЗГ '^■ “ ) а=г4^
где
■Ь<г> - ( - з '+ 5 Т —				•)(1" ¥			+ -	\|		♦.<«)-
Следовательно,		sin З2 —З sin г				__ г3ф1 (г)			_	ф! (г)
		sin З2 —З sin г				__ г3ф1 (г)			_	ф! (г)
	/(*) = (sin 2 —г) sin 2 ~~ г4ф, (2)									гф, (г)	*
и так	как ф ^ О ^ О ,		Чл (°) =£ 0,			то	точка		2 = 0 является простым
полюсом данной функции,				поэтому			ее вычет в этой				точке находим
по формуле (5)

res sin Зг —3 sin г\ г=о (sin г —г) sin 2)

П т - 2 Ь Ё L z:	Ф. (0)	1 = 24.
г - о г t i (г)	Ф, (0)	1 = 24.

Вычислить следующие вычеты:

з о 8 - s S	<л -	1 . 2 . . . . ) .		309.	res		.
з о 8 - s S	<л -	1 . 2 . . . . ) .			г;=0 (1 —cos г)2
(1 —cos 2г) sin г ‘				311.	res p b g Z)sh2 _
(1 —cos 2г) sin г ‘				-	г=_0 0		c0s2) sm*Z
312<flS0s^ (Л=2’ 3’			.).	-	*=°	ch z ^ 1 _ —
			.).	313.	res		г*
							2
П р и м е р 6.	Найти	вычеты функции / (г) =				у —	& ее особых

точках.

Р е ш е н и е . Особыми точками данной'функции будут 2=®1 н 2= 0. Точка 2 = 1 — простой полюс, поэтому

сМ*

res	/ (г) =
1	-1 U-1

Для установления характера	особой точки z = 0 разложим функцию
в ряд Лорана в окрестности этой точки. Имеем
Р*/г =	1	1
	21 га ^	3! г»

1 —z = l + z + z 2+ z 4 - ...

Перемножая эти ряды, получим

=	(■'1 +	г +	Ш	+	Ш	+■■)('1+ 'г + г+ * + -)■ =
	=	(1 +	2У +	^\|	+	• • •) ~ + С_2 ~ + .. . + правильная часть,
где с^ъФ 0,		k = 2, 3 ; ...
Таккак		главная часть ряда Лорана содержит бесконечное					мно
жество	членов с		отрицательными степенями z, то точка z = 0				яв
ляется	существенно особой точкой данной функции. Ее вычет в точке

z = 0 равен
^	o/(* )= * -l = i +	2i +	3T + - = * ~ i -
П р и м е р 7.	Найти вычет функции		/ (z) = cosz sin -- в ее особой
точке z = 0 .t
Р е ш е н и е .	Для установления характера особой			точки	разло
жим данную функцию в ряд Лорана			в окрестности	точки	z = 0.
Имеем
	Z2	Z*	•••
	COS2 = Г—— + -Jj		•••

j_ = 1 ___I__ j_I___

Sin z “ z

31 z»

Перемножая эти ряды, получим

m = c o . z s I n - i = ( l - . i i +

1 1

1- 2131 ‘ 41 51

01 31 2! 51 ^ 41 71 + -■

5! z\

1	51 z\
31 гз	51 z\
_ 1 _

...-(-правильная часть.

гз

Итак, ряд Лорана в окрестности точки z = 0 имеет вид

со.

“ " ■ " 4 "	2	(2я)Т(2п+~\|)ГГ + с- 7 +•••+—		,асть’
	п = 0
где с_ ( ) 'Ф 0,		к =	1 2 , ...	множество
Главная	часть		ряда Лорана содержит бесконечное	множество

членов, а значит, точка z = 0 —существенно особая точка данной

функции. Искомый

вычет равен

со

res (cos г sin

с_х

(2п)! (2п-Ь 1)! •

z « o \

* /

П р и м е р

Найти

вычет функции

, .

W = Z2 Sin — —г

в ее особой точке.

Z+1

точкой

данной

функции

является

точка

Р е ш е н и е . Особо»

—1.

Для

установления характера

этой точки

разложим функцию

ряд

Лорана в

окрестности

точки

z = —1. Для

этого

выразим г1

через

степени

разности г — (—]) = z +

Имеем

* =

[ < * + !) - !]* “ ( * + 1)я- 2 ( г + 1 ) + 1 .

(О

Ряд Лорана

для

функции

sin

* + 1

окрестности

точки

г —1

имеет

вид

sin

(2)

2 + 1

Z+1

31(2+1)»

г 5! (2 + I)5.

Перемножая (1) и (2), найдем

l(z + l)i

а (г + 1 )+ 1 ] £ г+ 1

3! (г +

,)а +

5|(г+1)».

- 3l ) 7 + Г +

3 !'(F+TF^lsi “ зг)(2 + 1)»+

• +

!—2 +

(г-|-1)1-

Ряд Лорана содержит бесконечное множество членов с отрица тельными степенями суммы z + 1 . Следовательно, точка z = — l яв ляется существенно особой точкой данной функции и ее вычет в этой точке равен

П р и м е р	9.	Найти	вычет функции
в точке г = 0.			/ (г) =	cos г
	Так как		вычет	в точке	г = 0 равен коэффициенту
Р е ш е н и е .
при г-1, то. сразу		получаем, что в данном случае этот вычет равен
нулю, поскольку		функция f (г) —четная			и ее разложение в окрест
ности точки '*=■=() не может содержать нечетных степеней г.
\ Найти вычеты в особых				точках	следующих функций:

314. /(г) =

315. /(г)«=г*е‘/*.

316.	/(г):	ell 2	317.		/(г) = -			е-
316.	/(г):	(2=4-1) ( г - 3 )	317.		/(г) = -
		(2=4-1) ( г - 3 )					—	sin-z
							—	sin-z
•318. /(г):		ег
•318. /(г):		> ( г - 1 Г	3 \|9 -		/ ( г )		(г + 1 )з(г _2)1 *
		> ( г - 1 Г	3 \|9 -		/ ( г )		(г + 1 )з(г _2)1 *
		_ I
320.	/(г) =	-2+ *	321.		/(г) = 22М!1				г1
322.	/ (г) =	cos ‘ + г3.	323.		/(г) =			sin 22
322.	/ (г) =	cos ‘ + г3.	323.		/(г) =		(z + t)		г - i \*
							(z + t)		г - i \*
324.	/(2):	1 — COS 2					„ ,	I
324.	/(2):	1 — COS 2		325.	f ( z ) =		e	*\
		га (г — 3) ’
		( 2 * - 1 ) ( г + 3 ) ‘		327.	/ (	2 ) =	- ^	- .
		( 2 * - 1 ) ( г + 3 ) ‘					2:) — - - Z2
							2:) — - - Z2
								2
328.	/(г) =	329	f	—		г~П	-	^	0
		2 — /	/		(2 — 1)" ' n			^	u
		ctg2 2 .	331.		/ ( 2) =		sin 2 cos

2 pZ— 1

I „ z

334. /(г) = e

1 + 2 '

336. /(г) =е~ sin

			sin	1
0 0 0 .	/			-
		^ —	j _ z .
з а ч	/ / 7			z
			2 2 + 1
335.	/ (2) =		e	2 .

§10. Теорема Коши о вычетах. Приложение вычетов

квычислению определенных интегралов. Суммирование некоторых рядов с помощью вычетов

Ь- Т е о р е м а Коши		о вычетах
Т о о р е м а.	Если функция	f (2) яв.гястся аналитической на гра
нице С области D и всюду внутри области, за исключением конечного
числа особых точек zL, z2, ... , zfl, то
	\ / (г) ilz =	2л 1 ^ res / (zk).
	д	^= I
П р и м е р	1. Вычислить	е	е- — 1
П р и м е р	1. Вычислить	интеграл \	— dz.

е-1

“2Г в

Р е ш е н и е . В области j z \|*< 4 функция	е*_1
Р е ш е н и е . В области j z \|*< 4 функция	/ (z^= -^ -j- аналитична
всюду, кроме точек z = 0 и г —— 1.
По теореме Коши о вычетах
^ - p ^ < k ? = 2 n t(re s /(0 ) +	res/(—1)).

|* j = 4

Точка z = 0 есть устранимая особая точка функции /(z), ибо

е* -1

1im —-— j—. г- • : 1 .

г-+0*(1+ 1)

Поэтому res/(0) = 0. Точка z = — 1—полюс первого порядка

r e s / ( - l ) = z l i mi { ^ Т Т ) ( г + 1) } = 1 - ^ 1- Таким образом,

Се*— 1 dz=2ni(\ — e_1). z2+ z

\Z \ z

П р и м е р	2.	Вычислить		интеграл		S	tgzdz.
.		В	области	D: \| г \| <	! z ! = 2			/ (г) =	tgz анали-
Р е ш е н и е .		В	области	D: \| г \| <	2 функция			/ (г) =	tgz анали-
тична всюду,	кроме			л		Л		*
тична всюду,	кроме		точек г = ^ и z = —			,	являющихся простыми
				л»		£		*
полюсами. Все другие особые точки гА=						их		*
полюсами. Все другие особые точки гА=						у + £л функции /(z)==tgz
лежат вне области D и поэтому не учитываются.
Имеем				sin z
		res /		sin z		= - i ,
		res /		(cosг)'	я	= - i ,
				sin z	~2
	res/			sin z			—	1.
	res/			(cos г)'	—	л /2	—	1.
Поэтому				(cos г)'	—	л /2
Поэтому
			5	tgzdz —— 4л/.
			\| 2 ; =»2
П р и м е р	3.	Вычислить		интеграл	I 2 — £ 1=3/2			z'-+\ dz.
					I 2 — £ 1=3/2
Р е ш е н и е .		В	области	D: \|z — / 1<		3/2	функция		/(z) = Z2+ 1

имеет две особые точки: z = i — полюс первого порядка и z = 0 — суще ственно особая точка.

По формуле (5) из § 9 имеем res/(/) = - 2z

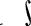
Для нахождения вычета в точке 2 = 0 необходимо иметь лорановское разложение функции /(z) в окрестности точки z = 0. Однако в дан ном случае искать ряд Лорана нет необходимости: функция /(г) чет ная, и поэтому можно заранее сказать, что в ее лорановском разло

жении будут содержаться только четные степени г и

Так что с_х = 0

и, следовательно,

res / (0) = 0.

По теореме Коши о "вычетах

2 8 + 1

I* — 21 — 3/2

П р и м е р 4. Вычислить интеграл

Р е ш е н и е . В круге | г ! ^ 2 подынтегральная функция имеет две особые точки z = l и z = 0. Легко установить, что z = l есть простой полюс, поэтому

Для установления характера особой точки 2= 0 напишем ряд

Лорана для функции - — j- sin — в окрестности этой точки. Имеем

= ~ ('1 “ ^ + 57 “ • • •) 7 + ^ + ^ + ''•'+пРавильная часть’ c_h Ф 0, k = 2, 3,

Так как ряд Лорана содержит бесконечное множество членов с отри цательными степенями z, то точка г = 0 является существенно особой. Вычет подынтегральной функции в этой точке равен

— — sin 1

Следовательно,

. 1

Вычислить интегралы:

337.^ ztgnzdz.

l*, =

338.

С:

^ /3+ ^ /3 = 3?/9'

339

•J

ег dz

340

-\ г —1

« * - 1 Td z .

г* (г+ 1 )-

z:<— iz-

1*1= 2

342•

sin яг

341.

г3 sin у dz.

г2 —г dz.

!*, —1/2

: = / з

344•

Г _ J г2 dz

12 + 1 1=4

siii3nг cos г

ez dz

*«■|12 i; = 4

345•

z4 +

2z2 +

1 '

COS

347.

: f +

I .

348.

2 * - 0 .

34».

{ ; £ » *

: f

» > - I .

35°-

J s r f J h

* .

31+ *■=•'*•

351.

f z sin z

J ,

JC2

*/*

C: T

352.

J p f j ,

C: A-4 -//2 =

2.V.

353.

z8sinydz.

r* i =

354.

(z +

\)e'/zdz.

|f |* 1/3

355.

fsin J

e*! cos z^ dz.

I * = 2 / 3 V

В ы ч е т ф у н к ц и и о т н о с и т е л ь н о б е с к о н е ч н о у д а л е н н о й т о ч к и

Говорят,

что

функция /(г)

аналитична в бесконечно

удаленной

точке г= о о ,

если

функция

аналитична в точке ц= 0.

Например,

функция

/ (г) =

sin

аналитична в точке

г = со, по

скольку функция

Ф (?)=/( ~ ) = sin£

аналитична

в точке £ = 0.

Пусть

функция

/(г)

аналитична

в некоторой

окрестности беско

нечно удаленной точки

(кроме самой

точки г = оо).

Точка 2 = оо называется изолированной особой точкой функции f(z),

если в некоторой

окрестности

этой

точки

нет

других особых точек

функции

/ (г).

Функция

^ (г)= = ^ -^

имеет в бесконечности

неизолированную осо

бенность:' полюсы

zk = kR этой

функции

накапливаются

в бесконеч

ности, если /г->оо.

Говорят, что 2= оо является

устранимой особой точкой, полюсом

или существенно особой точкой

функции f (z) в зависимости от того,

конечен,

бесконечен

или

вовсе

не существует

lim

/(г).

Критерии

типа

бесконечно

Z —*• оо

точки,

связанные

удаленной особой

с разложением Лорана,

изменяются

по сравнению с критериями для

конечных особых точек.

является

устранимой особой точкой

Т е о р е м а

Если г = со

функции

f (г),

то

лориновское

разложение / (г)

в окрестности этой

точки не содержит

положительных

степеней г;

если z = со— полюс,

то это разложение

содержит конечное число

положительных степе-

ней г, в случае существенной особенности —бесконечное число положи тельных степеней г.

При этом лорановским разложением функции / (г) в окрестности бесконечно удаленной точки будем называть разложение f (z) в ряд Лорана, сходящееся всюду вне круга достаточно большого радиуса R с центром в точке 2= 0 (кроме, быть может, самой этой точки г=оо).

Пусть функция / (г) —аналитична			в 'некоторой окрестности точки
2= оо (кроме, быть может, самой этой точки).
Вычетом функции f(z)		в бесконечности называют величину
	res/(со) =		Л	/ (г) </г,			(1)
			V”
где у~ —достаточно большая окружность 12 , =р,						проходимая	по
часовой стрелке (так что окрестность				точки	г= о о остается слева,
как и в случае конечной точки 2 = а).				вычет	функции в бесконеч
Из этого	определения	следует,	что
ности равен	коэффициенту	при г-1	в лорановском			разложении	/(г)

в окрестности точки z= o o , взятому с противоположным знаком:

	'res / (оо) = — c_i.			(2)
П р и м е р 5.		2J_ 1	имеем / (г) =	1
П р и м е р 5.	Для функции / (г) = — —		имеем / (г) =	1 -\|— . Это
выражение можно	рассматривать как	Z	лорановское	2
выражение можно	рассматривать как	ее	лорановское	разложение
в окрестности бесконечно удаленной точки. Имеем очевидно, что
	Тип /( r ) =	1,
	2 —* СО

так что точка z==oo является устранимой особой точкой, и мы пола

гаем, как обычно, /(о о )= 1 . Здесь ^ = 1		и,	следовательно,
res / (оо) =	—	1.
Из этого примера следует, что	вычет		аналитической функции

относительно бесконечно удаленной устранимой особой точки, в отли

чие от конечной устранимой		особой	точки, может		оказаться		отлич
ным от нуля.	разложения	функций	ег,	sin z, cos z,	shz,	chz	можно
Известные
рассматривать	также как	лорановские		разложения в		окрестности

точки z==oo. Так как все эти разложения содержат бесконечное мно

жество положительных Степеней z, то перечисленные функции имеют
в точке z = o o	существенную особенность.
Т е о р е м а	2. Если функция f (z) имеет в расширенной комплекс

ной плоскости конечное число особых точек, то сумма всех ее вычетов, включая и вынет в бесконечности, равна нулю.

Так что если		alt а.„ ...,	— конечные	особые точки	функции
/(г), то			п
			п
		res / (со)	2 re s/(a A) =	0
		res / (со) =	— 2 res / (о*).		(3)
			/г = 1
Последнее соотношение бывает удобно использовать при					вычисле
нии некоторых	интегралов.
- П р и м е р	6.	Вычислить интеграл

/ =

1+2* в

12=3 2 Р е ш е н и е . Полюсами (конечными) подынтегральной функции

	/ »		1 + 2*
			1 + 2*
являются корни zlt	z2, z3, z4	уравнения		z*= —1,	которые все лежат
внутри окружности	\|z ; = 2.		Функция	/(z )=	в окрестности

1+ 2

бесконечно удаленной точки имеет разложение

р / \	1	1	\_____ 1		_	1	_1_
^	1 +z*	Z4	1+	1	Z4	Z8	■212‘
			1+

нз котороговидно, что res / (оо) = — = 0. В силу равенства (3)

/ = 2ni 2 res / (zk) = — 2л1 res / (оо) == 0.

к= \

Пр и м е р 7. Вычислить интеграл

/:f==	[	____	- dz.
	J	(*+2)(2* + 3)<
I	г	=3j

Р е ш е н и е . Подынтегральная функция

z”

7 W - ;(г*+ 2)® (*>4-3)*

внутри окружности | z | = 3 имеет пять особых точек, являющихся кратными полюсами. Использование основной теоремы о вычетах при водит к большим вычислениям. Для вычисления данного интеграла удобнее использовать равенство (3), в силу которого будем иметь

				I —— 2лI res f (оо).					(3')
Так как функцию /(z)				можно представить в виде
	*17
(*». +2)3(28+3)4
				2».				1
				Z“	Z»
то отсюда	видно,		что	правильная		часть	лорановского разложения
этой функции		в окрестности			бесконечно удаленной точки z = co начи
нается с члена		1/z. Следовательно,				res/(oo) = —1.		Подставляя эту
величину в равенство (3), получим						/ = 2.щ.
Определить характер бесконечно удаленной точки для
следующих функций:
356.	/(г) = — ~ t z+ l . 357.						=
358.	/(2) =		-J .		359. f(z) = cos j .
360.	f(z) = ev*.				3 6 1 . f(z) = ze1/.				/ (г) =
	Пусть		функция		/(г)	представима		в виде
= ф (--). где функция					ф (£) — аналнтична			в точке	1— 0.
Доказать, что			res /(г) = — ф'(0).

<<< < Предыдущая 2 3 4 5 6 7 8 9 10 11 12 1314 / 4514 15 16 17 18 19 20 21 22 23 24 25 26 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
15.11.202212.46 Mб81225.pdf
#
15.11.202212.48 Mб81226.pdf
#
15.11.202212.5 Mб31227.pdf
#
15.11.202212.62 Mб21230.pdf
#
15.11.202212.64 Mб21232.pdf
#
15.11.202212.71 Mб71235.pdf
#
15.11.202212.77 Mб121236.pdf
#
15.11.202212.77 Mб31237.pdf
#
15.11.202212.8 Mб11240.pdf
#
15.11.202213.03 Mб131245.pdf
#
15.11.20224.76 Mб21246.pdf