Завдання 10.
Розв’язати систему лінійних алгебраїчних рівнянь методом Гауса, за правилом Крамера, за допомогою оберненої матриці. Перевірити правильність обернення матриці та розв'язання системи.
Розв’язання:
1. Розв'яжемо систему методом Гаусса - метод послідовного виключення змінного. Для компактності запису скористаємося розширеною матрицею. Перетворимо її до діагонального виду.
=
~
Отримаємо
систему трикутного вигляду:
,
звідки:
(2; -1 ;-3)
2. Розв'яжемо систему методом Крамера – складемо і обчислимо 4 визначника:
Головний:
,
Допоміжні:
,
,
,
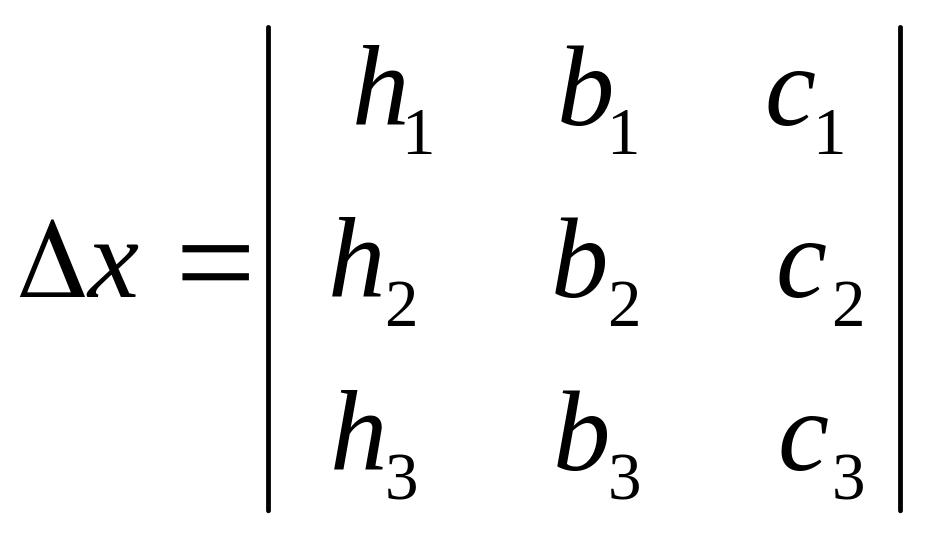
Відповідь: (2; - 1; -3)
3. Розв'яжемо систему за допомогою зворотньої матриці. Розв'яжемо матричне рівняння:
,
,
;
;
,
Апром.
-
проміжна
матриця з алгебраїчних доповнень
елементів матриці системи , А* - транспонована матриця.
де - мінори.
; ;
;
.
, , - обернена матриця.
;
Перевірки:
1)
Обертання матриці:
=
Отже, обернена матриця знайдена вірно.
2)
Тобто система розв’язана вірно.
Відповідь:
Контрольна робота №2.
Завдання 1.
Знайти: 1) довжину ребра AB; Величини кутів:
2) між ребрами AB і AD,
3) між гранями ABC і ADC,
4) між ребром AD і гранью ABC.
5) Площу грані ABC. 6) Об’єм піраміди АВСД.
7) Обчислити довжину висоти, з вершини Д на
грань ABC.
8) Проекцію точки D на грань ABC;
Скласти рівняння:
9) Прямої, що проходе скрізь точку C, паралельно ребру AD;
10) Прямої, що проходе скрізь точку В і перпендикулярної ребру АВ 11) Рівняння площини, що проходе скрізь точку С і перпендикулярної ребру АВ пірамиди.
12) Побудувати піраміду у просторі ( x;y;z).
Вершини піраміди відомі:
A ( -2;0;-1) |
B (0; 0; 4) |
C (1; 3; 2 ) |
D (3; 2; 7 ) |
Розв’язання:
1)Довжину ребра знайдемо як відстань між двома точками:
,
=
=
,
од.
2) Знайдемо напрямні вектори прямих, що містять ребра АВ, АС, АД
= (0 – (-2); 0 – 0; 4 –
(-1)) = (2; 0; 5)
= (1 – (-2); 3 – 0; 2 –
(-1)) = (3; 3; 3)
= (3 – (-2); 2 – 0; 7 –
(-1)) = (5; 2; 8)
Кут між ребрами дорівнює куту між прямими, що утримують ці ребра, тобто між напрямними векторами цих прямих. Застосуємо скалярний добуток векторів:
3) Кут між гранями дорівнює куту між площинами, що утримують ці грані, тобто дорівнює куту між нормальними векторами цих площин.
Нехай
Складемо рівняння
цих граней (АВС):
5(х+2)+3у+2(Z+1),
звідки
5х
+
3у
+
2Z
–
8
=
0;
(АDС):
=
,
-
2х
–
4
+
у
+ Z
+
1=
0
;
2х
–
Z +
3
=
0
,
,
4)
,
кут між ребром і гранню.
5)
Грань
піраміди представляє собою трикутник
або половину паралелограму, побудованого
на двох неколінеарних векторах. Площу
знайдемо за допомогою векторного добутку
цих векторів
≈
9,5 од2,
оскільки
од2
6)Піраміда представляє собою шосту частину паралелепіпеда, побудованого на двох некомпланарних векторах. Застосуємо змішаний добуток цих векторів:
Vпір.
од3
7)
.
Довжина висоти:
т. к.
,
Перевірка:
7)Знайдемо координати проекції вершини D(3;2;7) на грань (АВС):
5х
-
3у
-
2Z
+
8
=
0;
Рівняння перпендикуляра
:
;
38
;
;
;
.
9)
Рівняння прямої,
що проходе
через вершину
С(1;3;2)
АD(5;2;8)
Пряма
повинна мати той же нормальний вектор,
що і задана пряма, тому
.
10)
Рівняння
прямої,
що проходе
через вершину:
В(0;0;4)
площині
(A;D;C):
2х-у-
Z
+
3
=
0;
,
оскільки нормаль площини є напрямляючим
вектором прямої, яку шукаємо.
11)
Рівняння прямої,
що проходе
через вершину:
С(1;3;2)
ребру
,
2х
+
5Z –
12
=
0.
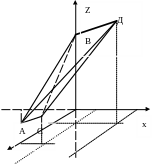
12) Побудуємо піраміду по точкам.
A ( -2;0;-1) |
B (0; 0; 4) |
C (1; 3; 2 ) |
D (3; 2; 7 ) |
Завдання 2.
Визначити та побудувати лінію,
рівняння якої має вигляд: .
Розв’язання:
Коефіцієнти
при
одного знаку, але різні,тому це рівняння
описує еліпс. Доведемо це.
,
,
.
Отримали
канонічне
рівняння еліпса
з центром в точці С(2;-3) і піввісями: по
ОХ
,
по ОУ
.
Відповідь: еліпс.
Завдання 3.
Дослідити лінійну залежність векторів:
, .
Розв’язання:
Знайдемо ранг матриці, складеної з координат векторів.
,
∆
=
=
=
=
- 6
.
Відповідь: Вектори , , лінійно незалежні.
Завдання 4.
Скласти рівняння лінії, для якої сума відстаней до точок
А(2;3) і В(4;5) дорівнює 54.
Розв’язання:
Візьмемо
довільну точку лінії. М(х;у)
ГМТ.
Згідно умові
.
Застосуємо формулу відстані між 2
точками:
,
тоді у
,
.
Відповідь:
окружность R=
5; C(3;4)
Контрольна робота №3.
Завдання 1.
Визначити ОДЗ функції: а) .