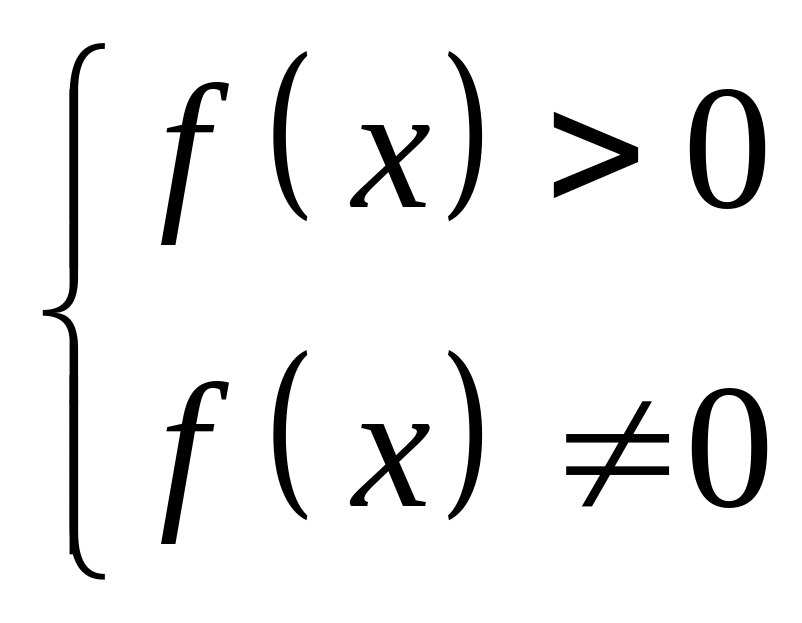- •І. Загальні положення
- •Уміння, на формування яких націлене навчання:
- •Стисла робоча програма (осінній семестр)
- •Тематика лекцій
- •2.2 Тематика практичних занять
- •Разом: 64 годин
- •Питання для самоперевірки
- •Навчальна література
- •Опорний конспект лекції „Визначники”
- •Характеристики визначників:
- •Властивості визначників:
- •Обчислення визначників
- •Конспект – схема лекції „Матриці”
- •Матриці
- •Характеристики матриць:
- •Властивості матриць:
- •Алгоритми знаходження оберненої матриці:
- •Ранг матриці
- •Методи визначення рангу матриць
- •Властивості рангу матриць:
- •Лінійна залежність
- •Конспект – схема лекції
- •Лінійні рівняння
- •Системи лінійних рівнянь
- •Види систем:
- •Елементарні перетворення системи
- •Критерій сумісності системи рівнянь
- •Методи розв’язання систем
- •Конспект – схема лекцій з
- •Вектори
- •Основні поняття
- •Характеристики змінних величин
- •Множини.
- •Дії над множинами
- •Область визначення (існування) функції – одз
- •Характеристики функцій:
- •Теорія границь
- •Означення границі
- •Властивості границь
- •Основні теореми про границі функцій
- •Нескінченно малі та нескінченно великі
- •Властивості еквівалентних функцій
- •Обчислення границь
- •Неперервність функцій
- •Точки розриву функції
- •Класифікація точок розриву
- •Правила відшукання точок розриву:
- •Модуль №1. Елементи лінійної алгебри
- •3.1.2. Практичні заняття
- •Методи цілеспрямованого формування у студентів уміння
- •Аналіз конкретних ситуацій.
- •Метод еврестичного дослідження (когнітивний).
- •11. Проблемний метод.
- •3.2. Види організації самостійної роботи, що виконуються студентами у позаурочний час.
- •Самостійні домашні роботи
- •Корекція самостійної роботи
- •Атестаційне тестування
- •Тест № 1
- •Тест № 2
- •Тест № 3
- •Тест № 4
- •Тест № 5
- •Тест № 6
- •Тест № 7
- •Тест № 8
- •Тест № 9
- •Тест № 10
- •Тест № 11
- •1.Визначте вид матриці (прямокутна , квадратна другого порядку, діагональна третього порядку, одинична третього порядку, нульова , матриця-стовпець, матриця-рядок):
- •Тест № 13
- •Тест № 14
- •Тест № 15
- •Тест № 1
- •Тест № 6
- •Тест № 7
- •5. Знайти геометричне місце точок, рівновіддалених від точок :
- •Тест № 8
- •Тест № 9
- •Тест № 11
- •Тест № 12
- •Тест № 13
- •Тест № 14
- •Тест № 15
- •Тест №1
- •Тест № 2
- •Тест № 3
- •Тест № 4
- •Тест № 5
- •Тест № 6
- •Тест № 8
- •Тест № 9
- •Тест № 10
- •Тест № 11
- •Тест № 12
- •Тест № 13
- •Тест № 15
- •Тест № 16
- •Тест № 17
- •Тест № 19
- •Тест № 20
- •Тест № 21
- •Тест № 22
- •2. Встановити, якою є функція (неперервною чи розривною)
- •Тест № 23
- •Тест № 24
- •Тест № 26
- •Тест № 27
- •Тест № 28
- •Тест № 29
- •Завдання 2.
- •Завдання 3.
- •2) По правилу трикутника:
- •3) По правилу Саруса:
- •4) Штучного доповнення:
- •Завдання 6.
- •Завдання 7.
- •Завдання 8.
- •Завдання 9.
- •Завдання 10.
- •Розв’язання:
- •Розв’язання:
- •Розв’язання:
- •Розв’язання:
- •Додаток 3. Допуск (перевірка готовності) до лекцій:
- •Тема „Матриці”
- •Тема „Системи лінійних алгебраічних рівнянь”
Область визначення (існування) функції – одз
Це
сукупність всіх допустимих значень
незалежної змінної, тобто це множина
дійсних значень х, при яких функція
має сенс.
|
|||
№ |
Вид функції |
Обмеження f(х) і g(х) існує |
Формулювання неможливого |
1 |
|
g(х) 0 |
Ділення на нуль. |
2 |
|
f(х) |
Добування коренів парних степенів з від’ємних чисел. |
3 |
|
f(х) > 0 |
Логарифмування недодатніх чисел |
4 |
|
|
В основі логарифма від’ємні числа та одиниця. |
5 |
|
f(х) |
Відшукання
|
6 |
|
f(х)
|
Відшукання
для
аргументів
|
7 |
|
f(х) |
Відшукання
|
8 |
|
f(х) 1 |
Відшукання
|
9 |
|
х- будь-яке |
Лише для n – натуральне можливо |
|
х
|
Лише для n – ціле від’ємне можливо |
|
|
х
|
Лише для n – додатнє не ціле |
|
|
х > 0 |
Лише для n – не ціле від’ємне можливо |
|
|
,
|
х |
Піднесення у степінь з іраціональним показником від’ємних чисел |
Способи задання функцій
1. Табличний. Недолік – неможна задати функцію цілком. |
2. Графічний. У деякій системі координат. |
3. Аналітичний – формулою (наявний або ненаявний, параметричний). |
4. Словесний. Дається правило складання функції.
Функція
Діріхле:
Зобразити графічно функцію не має можливості. |
|
Класифікація функцій
функцій за допомогою скінченого числа алгебраічних операцій (додавання, віднімання, множення, ділення) і суперпозиції функцій (взяття функції від функції).
2. Алгебраічні функції - мають 4 арифметичні операції.
1) Ціла раціональна функція – многочлен n степені.
Степень многочлена визначається найвищою степенню його одночленів. Корень многочлена – таке значення змінного ч, при якому многочлен перетворюється в нуль Р(х) = 0. Приведенним
є
многочлен
Теорема Даламбера, уточнив Гаус – доводе існування кореня у многочлена, не даючи методів знаходження його. Теорема
Безу:
Якщо число
Якщо
серед коренів є рівні, то вони кратні:
Правильна дріб – якщо степень чисельника нище степеня знаменника. Частинні
випадки:
1. Дробово – лінійна
2.
Обернена пропорційність
3) Іраціональна функція – алгебраічна функція з добування кореня n степеня.
α – іраціональне, , тригонометричні та обеонені тригонометричні.
Графіки прямої і оберненої функцій симетричні відносно прямої у = х.
Це результат послідовного застосування функцій. |