3.2.3. Модели случайных процессов в случае контроля потока продукции по количественному признаку

Рассмотрим простейший случай, когда единицы продукции – штучные, а поток – однорядный. Пусть контроль –операционный, Х – некоторый параметр изделия. Процесс Х(t) имеет, как прави- ло, нестационарный характер, так как техпроцесс постепенно разлаживается.

На рис. 5 приведены реализации нестационарного случайного процесса, когда разладка может происходить приблизительно по линейному закону, но в разных направлениях (хотя реализации бывают и более сложными: разладка сначала идет в одном направлении, а потом, под влиянием новых факторов, – в другом).

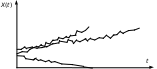
Рис. 5. Графики изменения значений параметра от изделия к изделию после наладки технологической линии

Простейшая модель такого процесса имеет вид: X(t) = А(t) + , где А(t) – некоторая функция (например, линейная) со случайными параметрами,  – случайная величина, распределенная по нормальному закону с нулевым математическим ожиданием и дисперсией ², которую обычно считают постоянной. Тогда при любом t случайная величина Х будет распределена также по нормальному закону, с той же дисперсией ², но со случайным математическим ожиданием А(t). Это распределение называется мгновенным. Дисперсия ² оценивается по нескольким малым выборкам (единицы продукции отбираются в выборку подряд) путем усреднения оценок дисперсий, полученных по каждой малой выборке.

Более сложная модель – когда ² зависит от t или от А(t).

Однако модели такого типа являются довольно «грубыми». Их использование основано на двух предположениях. Первое: если уж процесс стал развиваться в среднем по определенному (например, линейному) закону, то он так и будет продолжать развиваться по этому закону, т.е. неизменными будут даже коэффициенты. Второе: между параметрами Х₁, Х₂ соседних изделий корреляция отсутствует (поскольку  – случайная величина, а не процесс).

Более гибкая модель – это марковский процесс. Дискретный его вариант (марковская цепь) задается матрицей переходных вероятностей р_ij, т.е. вероятностей того, что случайно взятое изделие будет иметь значение Х = X_j, если предыдущее изделие имело значение Х = X_i (р_ij могут быть функцией «медленного» времени). Должны быть заданы также и априорные вероятности состояний X_i процесса в момент его настройки. Марковской цепью можно описывать и процесс изменения математического ожидания А(t), если X(t) представить в виде: X(t) =А(t) + .

Для описания процесса X(t) (обычно на сборочном конвейере) может быть использована также модель выбросов случайных процессов.

3.2.4. Модели случайных процессов в случае контроля последовательности партий продукции по количественному признаку

Пусть снова Х – некоторый параметр единицы продукции. Но t может иметь смысл номера партии и каждому t будет соответствовать столько значений Х, сколько единиц продукции в партии. Модель процесса целесообразно представлять в виде X(t) = А(t) + , где А(t) – случайный процесс изменения математического ожидания параметра Х среди единиц продукции одной партии, а случайная величина  по-прежнему имеет нулевое математическое ожидание, но может быть распределена не по нормальному закону, к тому же дисперсия ² (ее называют внутрипартионной) может представлять собой также случайный процесс D(t) или просто считаться случайной величиной на совокупности партий продукции.

Процессы А(t) и D(t) могут быть нестационарными и стационарными. Для описания нестационарных процессов более всего подходят марковские цепи, а стационарных – могут быть использованы и более простые -коррелированные случайные процессы, т.е. описываемые одномерными плотностями распределения w(a) и w(d) случайных величин А и D соответственно. При сильной (взаимной) корреляции между математическим ожиданием и дисперсией изделий одной партии в модель случайного процесса X(t) может быть введен еще и коэффициент взаимной корреляции. На рис. 6 представлена реализация а(t) стационарного случайного процесса А(t). Здесь показаны также плотности вероятности случайной величины Х на совокупности изделий одной партии – f(x) и нескольких партий – g(x). Между ними и плотностью w(a) при постоянной дисперсии ² и постоянном объеме партии имеется связь:

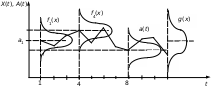
Рис. 6. График изменения среднего значения параметра от партии к партии – а(t), условные f_i(x) и полная g(x) плотности распределения