Раздел 1 за 34

Глава 2 36

Г 109

t* 85

R 85

Г 93

Е„ 107

' 0 / % 165

,Л. 201

Г? 346

га 363

Время, требуемое для завершения одного цикла сину­соиды называется периодом. Период обычно измеряется в секундах. Для обозначения периода используется буква t.

Количество циклов, совершаемых за заданный проме­жуток времени называется частотой. Частота синусоиды переменного тока обычно выражается в количестве циклов за секунду. Единицей частоты является герц. Один герц равен одному циклу в секунду.

Период синусоиды обратно пропорционален ее частоте. Чем выше частота, тем короче период. Соотношение меж­ду частотой и периодом синусоиды выражается следующи­ми формулами:

‘4 *4

где f — частота, at — период.

ПРИМЕР: Чему равна частота синусоиды с периодом

0. 05 секунд?

Дано: Решение:

f = 20 Гц.

ПРИМЕР: Если синусоида имеет частоту 60 герц, то чему равен ее период?

Дано:

f = 60 Гц

t - ?

Решение:

t

f 60

t = 0,0167 с или 16,7 мс.

Рис. 12-7. Колебание ^L-————* прямоугольной формы.

мгновенно достигают максимального значения и остают­ся такими в течение половины периода. Когда полярность изменяется, ток или напряжение мгновенно достигают противоположного пикового значения и остаются неиз­менными до конца следующей половины периода. Шири­на импульса равна половине периода. Ширина импульса

• это отрезок времени, в течение которого напряжение имеет свое пиковое или максимальное значение. Прямо­угольное колебание очень полезно как электронный сиг­нал, так как его характеристики могут быть легко изме­нены.

На рис. 12-8 показан один период колебания треуголь­ной формы. В течение первой половины периода сигнал возрастает по линейному закону от нуля до пикового зна­чения, а затем опять уменьшается до нуля. В течение вто­рой половины периода сигнал продолжает уменьшаться по линейному закону в отрицательном направлении до пико­вого значения, а после этого опять возрастает до нуля. Треугольные колебания используются главным образом как электронные сигналы.

Рис. 12-8. Колебание треугольной формы

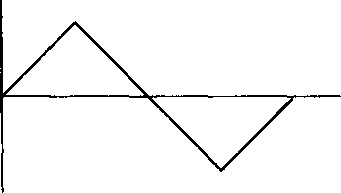
Рис. 12-9. Колебание пилообразной формы.

На рис. 12-9 показаны пилообразные колебания. Пило­образное колебание — это частный случай треугольного ко­лебания. Сначала величина напряжения или тока возрас­тает по линейному закону, а после этого быстро падает до своего отрицательного пикового значения. Участок с поло­жительным наклоном имеет относительно большую дли­тельность и меньший по абсолютной величине угол накло­на к оси времени, чем короткий участок. Пилообразные сигналы используются для переключения операций в элек­тронных цепях. В телевизорах и осциллографах они ис­пользуются для развертки электронного луча по экрану для создания изображения.

Импульсные колебания и другие несинусоидальные сигналы могут описываться двумя способами. Один метод рассматривает несинусоидальные сигналы как сумму скач­кообразных изменений напряжения, следующих через не­который интервал времени друг за другом. Второй метод рассматривает сигнал как алгебраическую сумму бесконеч­ного числа синусоид, имеющих различные частоты и ам­плитуды. Этот метод полезен при расчете усилителей. Если усилитель не может пропустить все синусоидальные час­тоты, то он искажает сигнал.

Несинусоидальные сигналы состоят из колебаний ос­новной частоты и гармоник. Основная частота соответ­ствует скорости повторения сигнала. Гармоники являют­ся синусоидами с более высокими частотами, которые кратны основной частоте. Четные гармоники имеют ча­стоты, которые являются произведениями четных чисел и основной частоты. Нечетные гармоники имеют частоты,

которые являются произведениями нечетных чисел и ос­новной частоты.

Прямоугольные колебания состоят из колебаний основ­ной частоты и всех нечетных гармоник.

Треугольные колебания также состоят из колебаний основной частоты и всех нечетных гармоник, но, в отли­чие от прямоугольных колебаний, нечетные гармоники сдвинуты по фазе на 180 градусов относительно колебания основной частоты.

Пилообразные колебания содержат как четные, так и нечетные гармоники. Четные гармоники сдвинуты на 180 градусов по фазе относительно нечетных гармоник.