32. 6. Вопросы

1. В чем различие между элементом ИЛИ и элементом ис­ключающее ИЛИ?

2. Нарисуйте символ, используемый для обозначения эле­мента исключающее ИЛИ.

3. Изобразите таблицу истинности для элемента исключа­ющее ИЛИ.

4. Нарисуйте символ, используемый для обозначения эле­мента исключающее ИЛИ-НЕ.

5. Запишите алгебраические выражения для операций ис­ключающее ИЛИ и исключающее ИЛИ-НЕ.

РЕЗЮМЕ

• На выходе элемента И появляется 1 тогда, когда на все его входы поступает сигнал 1.

• Элемент И выполняет операцию логического умножения.

• На выходе элемента ИЛИ появляется 1, если на любой из его входов подана 1.

• Элемент ИЛИ выполняет логическую операцию сложения.

• Элемент НЕ выполняет функцию, которая называется инверсией или отрицанием.

• Элемент НЕ преобразует входное состояние в противо­положное выходное состояние.

• Элемент НЕ-И является комбинацией элемента И и ин­вертора.

• Подача 0 на любой вход элемента НЕ-И дает на выходе 1.

• Элемент НЕ-ИЛИ является комбинацией элемента ИЛИ и инвертора.

• 1 на выходе элемента НЕ-ИЛИ появляется только тог­да, когда на оба входа поданы 0.

• 1 на выходе элемента исключающее ИЛИ появляется только тогда, когда уровни его входов различны.

• 1 на выходе элемента исключающее ИЛИ-НЕ появля­ется только тогда, когда уровни его входов одинаковы.

Гпава 32. Самопроверка

1. Нарисуйте схематическое обозначение шестивходово­го элемента И.

2. Изобразите таблицу истинности для четырехвходово­го элемента И.

3. Нарисуйте схематическое обозначение шестивходово­го элемента ИЛИ.

4. Изобразите таблицу истинности для четырехвходово­го элемента ИЛИ.

5. Каково назначение элемента НЕ?

6. Чем отличается инвертор для входного сигнала от ин­вертора для выходного сигнала?

7. Нарисуйте схематическое обозначение для восьмивхо­дового элемента НЕ-И.

8. Изобразите таблицу истинности для четырехвходово­го элемента НЕ-И.

9. Нарисуйте схематическое обозначение для восьмивхо­дового элемента НЕ-ИЛИ.

10. Изобразите таблицу истинности для четырехвходово­го элемента НЕ-ИЛИ.

11. В чем особенность элемента исключающее ИЛИ?

12. Какое максимальное количество входов может иметь элемент исключающее ИЛИ-НЕ?

Глава 33. Простые логические цепи

ЦЕЛИ

После изучения этой главы студент должен быть в со­стоянии:

• Объяснить назначение диаграмм Вейча.

• Описать, как использовать диаграммы Вейча для упро­щения Булевских выражений.

Цифровые цепи все больше и больше используются в электронике. Область их применения не ограничивается компьютерами, а распространяется на такие приложения, как техника измерений, автоматическое управление и ро­бототехника. Во всех этих приложениях необходимы слож­ные переключающие цепи, которые формируются на осно­ве пяти основных логических элементов: И, ИЛИ, И-НЕ, ИЛИ-НЕ и инвертора.

Отличительной чертой всех этих логических элементов является то, что они имеют только два рабочих состояния. Это ВКЛЮЧЕНО (1) или ВЫКЛЮЧЕНО (0). При соедине­нии логических элементов между собой для формирования более сложных цепей необходимо получить наиболее про­стую цепь из всех возможных.

Булева алгебра предлагает метод представления слож­ных переключающих функций в форме уравнений. Буле­во выражение является уравнением, которое связывает состояние выхода логической цепи с состоянием ее входов. Диаграммы Вейча обеспечивают быстрый и легкий способ приведения логического уравнения к его простейшему виду.

32. 1. ДИАГРАММЫ ВЕЙЧА

Диаграммы Вейча обеспечивают быстрый и легкий ме­тод приведения сложных быражений к их простейшей

форме. Они могут быть составлены для двух, трех или четырех переменных. На рис. 33-1 изображено несколько диаграмм Вейча.

Рис. 33-1. Диаграммы Вейча для двух, трех и четырех переменных.

Для того, чтобы использовать диаграмму Вейча, выпол­ните следующие шаги, которые иллюстрируются на при­мере.

1. Нарисуйте диаграмму, соответствующую числу перемен­ных.

2. Нанесите на нее логические .функции, отмечая их зна­ком X в соответствующем квадрате.

3. Для получения упрощенной логической функции объе­дините соседние квадраты, помеченные знаком X в группы по восемь, четыре или два. Продолжайте объе­динять до тех пор, пока не будут объединены все квад­раты, помеченные знаком X.

4. Логически сложите слагаемые (объедините с помощью операции ИЛИ) от каждой петли, одно слагаемое на каждую петлю. (Каждое слагаемое извлекается из ди­аграммы Вейча и логически суммируется с другими, например ABC + BCD.)

5. Запишите упрощенное выражение.

ПРИМЕР: Упростите АВ + АВ + АВ.

Шаг 1. Нарисуем диаграмму Вейча. Мы имеем две пе­ременных А и В, поэтому используем таблицу для двух переменных.

Шаг 2. Нанесем логические функции, помечая их зна­ком X в соответствующем квадрате.

+

АВ

Первое

слагаемое

АВ

Второе

слагаемое + АВ

Третье

слагаемое

А	А		А	А		А	А
X		В	X	X	В	X	X
		В			В	V \

Пометим первое слагаемое А В.

Пометим второе слагаемое АВ.

Пометим третье слагаемое АВ

Шаг 3. Объединим соседние квадра­ты, помеченные знаком X, в наибольшие возможные группы.

Проанализируем диаграмму — какая возможна наибольшая группа? Наиболь­шая возможная группа состоит из двух квадратов.

А *х	А X
X ICO

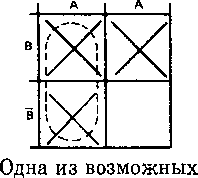
групп показана штриховой линией.

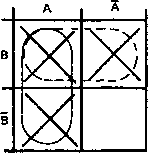
Другая возможная группа на этой диаграмме показана штриховой линией.

Шаг 4. Логически сложим эти группы (операция ИЛИ): или А, или В = А + В. _ _

Шаг 5. Упрощенным выражением для АВ + АВ + АВ = Y является А + В = Y, что получено из диаграммы Вейча.

ПРИМЕР: Найдите упрощенное выражение для

ABC + ABC + ABC + ABC = Y.

Шаг 1. Нарисуем диаграмму Вейча для трех переменных.

X

с с с Шаг 2. Пометим знаком X логические функции каждого слагаемого на диаграмме Вейча.

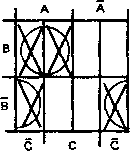
Шаг 3. Объединим сосед­ние квадраты в наиболь­шие возможные группы.

Шаг 4. Запишем слагаемые для каждо-й петли, одно сла­гаемое на каждую петлю:

АВ, ВС

Шаг 5. Упрощенным выражением является АВ + ВС = Y.

Отметим необычное объединение двух нижних квадра­тов. Четыре угла диаграммы Вейча считаются связанны­ми, как если бы диаграмма была свернута в шар.

ПРИМЕР: Найдите упрощенное выражение для:

ABCD + ABCD + ABCD + ABCD + ABCD + ABCD = Y.

Шаг 1. Нарисуем диаграмму Вейча для трех переменных.

		X	X
X		X	X
X

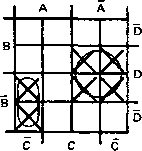•Шаг 2. Пометим знаком X Шаг 3. Объединим сосед- логические функции каждого ние квадраты в наиболь- слагаемого на диаграмме шие возможные группы.

Вейча.

Шаг 4. Запишем слагаемые для каждой петли, одно сла­гаемое на каждую петлю: AD, ABC.

Шаг 5. Для получения упрощенного выражения логи­чески сложим полученные слагаемые: AD + ABC = Y.