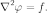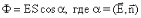1) Электрические заряды и их взаимодействие, закон Кулона.

Электрический заряд определяет свойство тел взаимодействовать с другими заряженными телами через электростатические поля, создаваемые этими зарядами.

Взаимодействие тел может быть положительным (если тела/заряды притягиваются) и отрицательным (если тела/заряды отталкиваются).

Очевидно существование элементарного заряда. Им обладают большинство частиц (протон, позитрон, электрон).

Заряд равен целому числу таких элементарных зарядов.

Если заряд неподвижен, то он в простанстве создает электростатическое поле. Если заряд двигается без ускорения – еще и магнитное поле. Если двигается с ускорением – электромагнитное поле, которое распространяется в виде электромагнитных волн.

Точечный заряд – заряженное тело, линейными размерами которого можно пренебречь.

Сила взаимодействия двух зарядов определяется по закону Кулона:

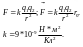
1. Заряд распределяется равномерно по всей длине.

Вводится понятие о линейной плотности заряда.

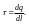
2. Заряд распределяется равномерно по поверхности заряженного тела.

Вводится понятие о поверхностной плотности заряда.

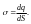
3. Заряд распределяется равномерно по всему объему.

Вводится понятие об объемной плотности заряда.

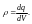
2) Напряженность – силовая характеристика, равная отношению силы, действующей со стороны этого поля, на точечный заряд, помещенный в данную точку.

Направление 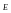совпадает с направлением

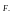
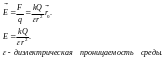
Электрическое поле — одна из составляющих электромагнитного поля, особый вид материи, существующий вокруг тел или частиц, обладающих электрическим зарядом, а также в свободном виде при изменении магнитного поля (например, в электромагнитных волнах). Электрическое поле непосредственно невидимо, но может наблюдаться благодаря его силовому воздействию на заряженные тела.

Напряженность поля точечного заряда.

Обозначим: q - заряд, создающий поле,

q₀ - заряд, помещенный в поле (внешний заряд).

Закон Кулона: 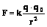 . Напряженность поля:  .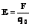

Тогда напряженность поля точечного заряда: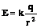 

Принцип суперпозиции.

Если в точке пространства существуют поля, создаваемые несколькими зарядами, то напряженность в данной точке поля равна векторной сумме напряженностей полей.

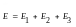
3) Потоком вектора напряженности наз. величина Ф, равная произведению модуля вектора напряженности на площадь контура S, ограничивающую некоторую площадь, и на косинус угла между вектором напряженности и нормалью (перпендикуляром) к площадке.
Если считать, что напряженность пропорциональна числу силовых линий, приходящихся на единицу площади поверхности (т.е. густоте), то поток напряженности пропорционален полному числу силовых линий, пересекающих данный контур.

Теорема Гаусса — основная теорема электродинамики, которая применяется для вычисления электрических полей, входит в систему уравнений Максвелла. Она выражает связь между потоком напряжённости электрического поля сквозь замкнутую поверхность и зарядом в объёме, ограниченной этой поверхностью

Теорема Гаусса. Поток вектора напряженности через замкнутую поверхность равен алгебраической сумме зарядов, охватываемой этой суммой зарядов, деленной на проницаемость среды и электрич. постоянную.

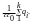
В работе Остроградского формула записана в следующем виде:

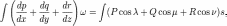
где ω и s — дифференциалы объёма и поверхности соответственно. В современной записи ω = dΩ — элемент объёма, s = dS — элемент поверхности. 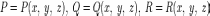  — функции, непрерывные вместе со своими частными производными первого порядка в замкнутой области пространства, ограниченного замкнутой гладкой поверхностью.

4)Теорема применяется для расчета электростатических полей.

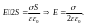
1. Поле бесконечно длинного заряженного цилиндра.

заряд распределен по всей длине

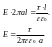
заряд распределен по всей поверхности

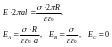
2. Поле заряженной сферы.

заряд распределен по всей поверхности

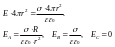
заряд распределен по всему объему

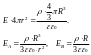
3.Поле заряженной плоскости

Рассмотрим поле, создаваемое бесконечной однородной заряженной плоскостью. Пусть поверхностная плотность заряда плоскости одинакова и равна σ. Представим себе мысленно цилиндр с образующими, перпендикулярными к плоскости, и основанием ΔS, расположенным относительно плоскости симметрично. В силу симметрии E' = E'' = E. Поток вектора напряжённости равен 2EΔS. Применив теорему Гаусса, получим:

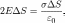из которого

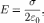
5) Потенциальность постоянного электрического поля.

Работа силы F на элементарном перемещении dl равна

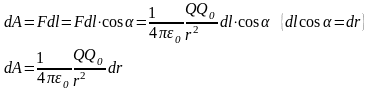
Работа при перемещении Q₀ из точки 1 в точку 2.

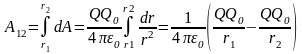не зависит от траектории перемещения. Следовательно эл.стат. поле точечного заряда является потенциальным, а эл.стат. силы консервативными.

Потенциал в какой либо точке эл.стат. поля есть физическая величина, определяемая потенциальной энергией положительного заряда, помещённого в эту точку.

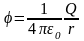
Разность потенциалов двух точек равна работе при перемещении единичного положительного заряда из точки 1 в точку 2.

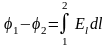
Напряжённость электрического поля точечного заряда

Согласно формуле Гаусса — Остроградского, а также используя уравнениеМаксвелла 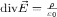 , легко получить:

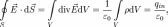
где q_in — заряд, находящийся внутри замкнутой поверхности S, объемом V. В качестве поверхности интегрирования возьмем сферу (центральная симметрия), тогда

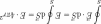
В силу центральной симметрии поля точечного заряда:

.

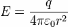6) Потенциал, связь между напряженностью и потенциалом.

Потенциал – энергетическая характеристика поля, численно равная работе, которую нужно совершить, чтобы переместить точечный заряд из данной точки в бесконечность.

Ввиду того, что работа – скалярная величина, и потенциал – скаляр.

Понятие о потенциале можно ввести для электростатического поля ввиду того, что работа по перемещению заряда не зависит от формы траектории, по которой осуществляется перенос, а только от положения точки.

Примечание автора. Путем графической иллюстрации и вывода формул была получена следующая формула.

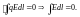
Циркуляция вектора Е вдоль замкнутого контура равна нулю.

Циркуляция – необходимое и достаточное условие для введения скалярного потенциала. Доказательством является независимость работы от вида движения и формы траектории.

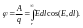Следует, что математически потенциал – интеграл от напряженности электрического поля. Отсюда, напряженность – производная от потенциала.

Тогда, учитывая, что ориентирован в пространстве,

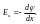
«Минус» означает, что действующая сила (напряженность) направлена в сторону убывания потенциала, то есть туда, где потенциальная энергия заряда будет иметь наименьшую величину.

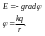
Эквипотенциальная поверхность — понятие, применимое к любому потенциальному векторному полю, например, к статическому электрическому полю или к ньютонову гравитационному полю. Эквипотенциальная поверхность — это поверхность, на которой скалярный потенциал данного потенциального поля принимает постоянное значение.

В трёхмерной декартовой системе координат уравнение принимает форму:

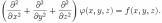
В декартовой системе координат оператор Лапласа записывается в форме   и уравнение Пуассона принимает вид: