25.Магнитное поле кругового контура с током.

. Магнитное поле кругового тока.

Г рафическая иллюстрация. Окружность, по которой течет ток. Отмечен радиус и отрезок dl.

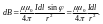
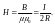
Графическая иллюстрация. Окружность, по которой течет ток. Отмечен радиус, точка в пространстве («на оси»), расстояние от центра окружности до нее – h.

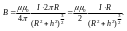
Магнитный момент витка с током -

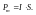
Отметим, что это векторная величина и вектор направлен вдоль оси витка с током в ту же сторону, что и вектор магнитной индукции.

26. Поток магнитной индукции. Теорема Гаусса Для вектора магнитной индукции в интегральной и дифференциальной формах.

Магнитный поток.

П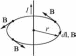 оток вектора магнитной индукции через площадку dS – физическая величина, равная произведению величины этой площадки и проекции вектора м.и. на направление положительной нормали этой площадки.

Если поле однородное, а поверхность плоская (расположена перпендикулярно к В), то магнитный поток:

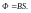
Единица измерения – Вебер [Вб].

Теорема Гаусса.

Магнитный поток через произвольную замкнутую поверхность равен нулю.

Таким образом, теорема показывает, что в природе не существует магнитных зарядов.

1 Вебер – такой магнитный поток, который равномерно изменяясь за единицу времени наводит в контуре, который он пронизывает, ЭДС равную 1 В.

Работа по перемещению проводника с током в магнитном поле.

Графическая иллюстрация.

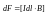Эта сила – сумма всех сил Лоренца, действующих на движущиеся заряды в проводнике.

Под ее действием проводник смещается или деформируется.

Если 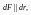угол равен нулю:

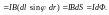
Р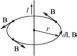 абота по перемещению проводника с током определяется произведением тока на изменение магнитного потока.

Это выражение справедливо для криволинейного или для замкнутого проводника любой формы.

Графическая иллюстрация.

Пара сил создает вращающий момент.

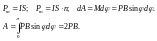
27.Теорема о циркуляции вектора магнитной индукции в интегральной и дифференциальной формах.

В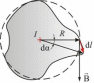 озьмем контур l (рис. 2.8), охватывающий прямой ток I, и вычислим для него циркуляцию вектора магнитной индукции , т.е. 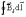. Вначале рассмотрим случай, когда контур лежит в плоскости перпендикулярно потоку (ток I направлен за чертеж). В каждой точке контура вектор направлен по касательной к окружности, проходящей через эту точку (линии прямого тока – окружности). Воспользуемся свойствами скалярного произведения векторов.

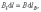где 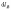– проекция dl на вектор , но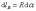 , где R – расстояние от прямой тока I до dl. 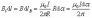Отсюда

это теорема о циркуляции вектора : циркуляция вектора магнитной индукции равна току, охваченному контуром, умноженному на магнитную постоянную. Иначе обстоит дело, если ток не охватывается контуром (рис. 2.9).

При обходе радиальная прямая поворачивается сначала в одном направлении (1–2), а потом в другом (2–1). Поэтому , и следовательно

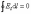
Итак, 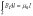, где I – ток, охваченный контуром L.

Эта формула справедлива и для тока произвольной формы, и для контура произвольной формы.

Если контур охватывает несколько токов, то т.е. циркуляция вектора равна алгебраической сумме токов, охваченных контуром произвольной формы.

Теорема о циркуляции вектора индукции магнитного поля 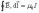позволяет легко рассчитать величину В от бесконечного проводника с током (рис. 2.10): .

Итак, циркуляция вектора магнитной индукции отлична от нуля, если контур охватывает ток (сравните с циркуляцией вектора : ).

Такие поля, называются вихревыми или соленоидальными.

Магнитному полю нельзя приписывать потенциал, как электрическому полю. Этот потенциал не был бы однозначным: после каждого обхода по контуру он получал бы приращение . Линии напряженности электрического поля начинаются и заканчиваются на зарядах. А магнитных зарядов в природе нет. опыт показывает, что линии всегда замкнуты (см. рис. 1.2. и 1.7). Поэтому теорема Гаусса для вектора магнитной индукции записывается так: .
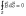