4. 2. Вопросы

1. Запишите закон Ома в виде формулы.

2. Какова величина тока в цепи сопротивлением 2400 ом, к которой приложено напряжение 12 вольт?

3. Какова должна быть величина сопротивления для того, чтобы ограничить ток 20 миллиамперами при прило­женном напряжении 24 вольта?

4. Какое напряжение необходимо приложить, чтобы обес­печить силу тока 3 ампера через сопротивление 100 ом?

4. 3. ПРИМЕНЕНИЕ ЗАКОНА ОМА

В последовательной цепи (рис. 5-12) через всю цепь те­чет один и тот же ток.

Рис. 5-12. В последова­тельной цепи сила тока одинакова во всей цепи.

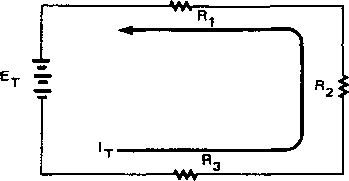Полное напряжение, приложенное к последовательной цепи, равно сумме падений напряжений на отдельных на­грузках (сопротивлениях) цепи.

Ет = Е_к +

+ Е_Кз +■ • -+E_Rn

Общее сопротивление последовательной цепи равно сум­ме отдельных сопротивлений цепи.

R_T = Rj + R₂ + R₃+. • .+R_n.

В параллельной цепи (рис. 5-13) одинаковое напряже­ние прикладывается к каждой ветви цепи.

ТЛ ТЛ 171 171

т - Rj - - -Ь_Кз - £i_Rn .

Полный ток в параллельной цепи равен сумме токов от­дельных ветвей цепи.

Величина обратная полному сопротивлению равна сум­ме обратных величин сопротивлений отдельных ветвей.

1 _ 1 1 R_T Rj R₂ R3 R_n

Общее сопротивление параллельной цепи всегда мень­ше, чем наименьшее из сопротивлений отдельных ветвей.

Рис. 5-13. В парал­лельной цепи токи делятся между вет­вями цепи и скла­дываются при воз­вращении в источ­ник тока.

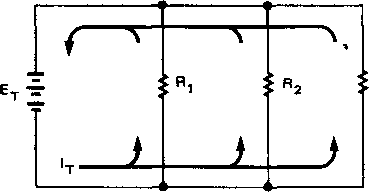
Закон Ома утверждает, что ток в цепи (последователь­ной, параллельной или последовательно-параллельной) прямо пропорционален напряжению и обратно пропорцио­нален сопротивлению.

i = l.

R

При определении неизвестных величин в цепи, следуйте следующим правилам:

1. Нарисуйте схему цепи и обозначьте все известные ве­личины.

2. Проведите расчеты для эквивалентных цепей и перери­суйте цепь.

3. Рассчитайте неизвестные величины.

Помните: закон Ома справедлив для любого участка цепи и может применяться в любой момент. По последо­вательной цепи течет один и тот же ток, а к любой ветви параллельной цепи приложено одинаковое напряжение.

ПРИМЕР. Чему равен полный ток в цепи, изображен­ной на рис. 5-14 ?

Дано:

I = ?

Е_т = 12 В R_T = ?

Rj = 560 Ом R₂ = 680 Ом R₃ = 1 кОм = 1000 Ом.

-AW-

560 Ом

■jfc Е_т = 12 В R₂«6800m:

i , l_T-7 R₃ = 1 k°m

Рис. 5-14. Решение:

Сначала вычислим общее сопротивление цепи: R_T = R_t + R₂ + R₃ R_T = 560 + 680 + 1000 = 2240 Ом.

■Wr

Нарисуем эквивалентную цепь. См. рис. 5-15.

Л

Е_т = 12 В

'т = ^?

Рис. 5-15.

R_T = 2240 Ом:

Теперь вычислим полный ток: Е_т 12

1_Т -

R_T 2240

1_Т = 0,0054 А или 5,4 мА.

ПРИМЕР. Каково падение напряжения на резисторе R₂ в цепи, изображенной на рис. 5-16?

Дано:

Е_т = 48 В R_T = ?

Rj = 1,2 кОм - - 1200 Ом R₂ = 3,9 кОм = 3900 Ом R₃ = 5,6 кОм = 5600 Ом.

-ANV

1,2 кОм

Рис. 5-16. Решение:

Сначала вычислим общее сопротивление цепи:

R_T = R, + R₂ + R₃

R_T = 1200 + 3900 + 5600 = 10700 Ом. Нарисуем эквивалентную цепь. См. рис. 5-17.

R_T = 10700 0м

I

Е_т = 48 В

Т и. 'т^=;

Теперь вычислим полный ток:

48

Е_т

R-г

10700

I_T = 0,0045 А или 4,5 мА

Вспомним, что в последовательной цепи один и тот же ток течет через всю цепь. Следовательно, I_R = 1_т.

Е„

R,

Е„

0. 0045 =

3900

Е₂ = (0,0045)(3900)

Е₂ = 17,55 В.

ПРИМЕР. Чему равно значение R₂ в цепи, изображен­ной на рис. 5-18?

|ет * 120 В
J 1 , 1т- 200 мА	;R1= 1кОм ; >■— - - —'	:R2 ■7 ij

>3 “ 5,6 кОм

Рис. 5-18.

Сначала найдем ток, протекающий через R_x и R_r По­скольку к каждой ветви параллельной цепи приложено одинаковое напряжение, напряжение на каждой ветви равно напряжению на источнике тока и равно 120 вольт.

Ri

Ri

Дано:

E_Ri = 120 В Rj = 1000 Ом.

Дано:

E_r = 120 В

Решение:

Е

120 1000

1^ =0,12 А.

Решение:

Е_в

R,

I_R =0,021 А.

R₃ = 5600 Ом.

В параллельной цепи полный ток равен сумме токов в ветвях.

Решение:

Теперь с помощью закона Ома можно найти величину резистора R₂.

Дано: Решение:

Ег,

R,

120

R,

0,059 =

Дано:

1_Т = 0,200 А

1^ =0,12 А

Ч=^?

I_R =0,021 А.

I_Rg = 0,059 А E_Ra = 120 В

R₂²=?

Irp 1тЭ "Ь 1р "Ь In

I Z “3

0. 200 = 0,12 + I_R + 0,021

0. 200 = 0,141 + I_R

0. 200 - 0,141 = I_R²

0. 059 А = 1^.

Ro

120

0,059

R₂ = 2033,9 Ом.

ПРИМЕР. Чему равен ток через резистор R_g в цепи, изображенной на рис. 5-19 ?

Рис. 5-19.

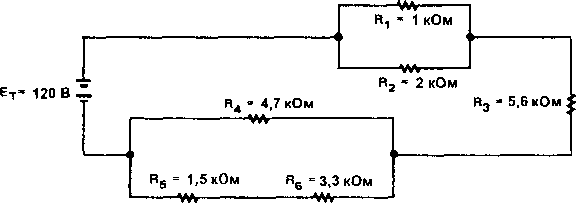
Сначала определим эквивалентное сопротивление (R_A) резисторов R_x и R₂.

1 1

1

R, R,

Дано: Решение:

1

Ri

R_x = 1000 Ом

R₂ = 2000 Ом.

+

1000

2000

Ra

Ra

2000

R_a = 666,67 Ом.

Теперь найдем эквивалентное сопротивление (R_B) рези­сторов R₄, R₅ и R₆. Сначала найдем общее сопротивление (R_g) последовательно соединенных резисторов R₅ и R₆.

+

J.

R

Дано:

R_s = ^?

R₅ = 1500 Ом R_K = 3300 Ом.

ь

Дано:

R₄ = 4700 Ом R₀ = 4800 Ом.

Решение:

R«

R_c = 1500 + 3300 = 4800 Ом.

Решение:

J_ ₌ JL

R„ R,

R«

(В этом случае общий знаме­натель найти

1

• сложно.

_в 4700 4800 Будем исполь­зовать деся­тичные дроби.)

1

Rr

= 0,000213 + 0,000208

1

R_B =

0,000421 R_B = 2375,30 Ом.

Нарисуем эквивалентную цепь, подставляя R_A и R_B, и найдем полное сопротивление последовательной эквивален­тной цепи. См. рис. 5-20.

Г

УЛ

R_a = 666,67 0м

R_B = 2375,3 0м W,

Rg = 5,6 кОм

Решение:

Rt=R_a+R₃ + Rb

R_a = 666,67 Ом R_T = 666,67 + 5600 + 2375,30 R₃ = 5600 Ом R_T = 8641,97 Ом.

R_B = 2375,30 Ом.

Теперь с помощью закона Ома найдем общий ток в эк­вивалентной цепи.

Дано: Решение:

I_T = ? I ₌ Цт ₌ 120

Е_т = 120 В Rt 8641,97

R_T = 8641,97 Ом. 1_т = 0,0139 А или 13,9 мА.

В последовательной цепи по всей цепи протекает оди­наковый ток. Следовательно, ток, протекающий через R₃, равен общему току в цепи.

Ir₃ = It ⁼ 13,9мА.