
- •Brief Contents
- •Contents
- •Preface
- •Who Should Use this Book
- •Philosophy
- •A Short Word on Experiments
- •Acknowledgments
- •Rational Choice Theory and Rational Modeling
- •Rationality and Demand Curves
- •Bounded Rationality and Model Types
- •References
- •Rational Choice with Fixed and Marginal Costs
- •Fixed versus Sunk Costs
- •The Sunk Cost Fallacy
- •Theory and Reactions to Sunk Cost
- •History and Notes
- •Rational Explanations for the Sunk Cost Fallacy
- •Transaction Utility and Flat-Rate Bias
- •Procedural Explanations for Flat-Rate Bias
- •Rational Explanations for Flat-Rate Bias
- •History and Notes
- •Theory and Reference-Dependent Preferences
- •Rational Choice with Income from Varying Sources
- •The Theory of Mental Accounting
- •Budgeting and Consumption Bundles
- •Accounts, Integrating, or Segregating
- •Payment Decoupling, Prepurchase, and Credit Card Purchases
- •Investments and Opening and Closing Accounts
- •Reference Points and Indifference Curves
- •Rational Choice, Temptation and Gifts versus Cash
- •Budgets, Accounts, Temptation, and Gifts
- •Rational Choice over Time
- •References
- •Rational Choice and Default Options
- •Rational Explanations of the Status Quo Bias
- •History and Notes
- •Reference Points, Indifference Curves, and the Consumer Problem
- •An Evolutionary Explanation for Loss Aversion
- •Rational Choice and Getting and Giving Up Goods
- •Loss Aversion and the Endowment Effect
- •Rational Explanations for the Endowment Effect
- •History and Notes
- •Thought Questions
- •Rational Bidding in Auctions
- •Procedural Explanations for Overbidding
- •Levels of Rationality
- •Bidding Heuristics and Transparency
- •Rational Bidding under Dutch and First-Price Auctions
- •History and Notes
- •Rational Prices in English, Dutch, and First-Price Auctions
- •Auction with Uncertainty
- •Rational Bidding under Uncertainty
- •History and Notes
- •References
- •Multiple Rational Choice with Certainty and Uncertainty
- •The Portfolio Problem
- •Narrow versus Broad Bracketing
- •Bracketing the Portfolio Problem
- •More than the Sum of Its Parts
- •The Utility Function and Risk Aversion
- •Bracketing and Variety
- •Rational Bracketing for Variety
- •Changing Preferences, Adding Up, and Choice Bracketing
- •Addiction and Melioration
- •Narrow Bracketing and Motivation
- •Behavioral Bracketing
- •History and Notes
- •Rational Explanations for Bracketing Behavior
- •Statistical Inference and Information
- •Calibration Exercises
- •Representativeness
- •Conjunction Bias
- •The Law of Small Numbers
- •Conservatism versus Representativeness
- •Availability Heuristic
- •Bias, Bigotry, and Availability
- •History and Notes
- •References
- •Rational Information Search
- •Risk Aversion and Production
- •Self-Serving Bias
- •Is Bad Information Bad?
- •History and Notes
- •Thought Questions
- •Rational Decision under Risk
- •Independence and Rational Decision under Risk
- •Allowing Violations of Independence
- •The Shape of Indifference Curves
- •Evidence on the Shape of Probability Weights
- •Probability Weights without Preferences for the Inferior
- •History and Notes
- •Thought Questions
- •Risk Aversion, Risk Loving, and Loss Aversion
- •Prospect Theory
- •Prospect Theory and Indifference Curves
- •Does Prospect Theory Solve the Whole Problem?
- •Prospect Theory and Risk Aversion in Small Gambles
- •History and Notes
- •References
- •The Standard Models of Intertemporal Choice
- •Making Decisions for Our Future Self
- •Projection Bias and Addiction
- •The Role of Emotions and Visceral Factors in Choice
- •Modeling the Hot–Cold Empathy Gap
- •Hindsight Bias and the Curse of Knowledge
- •History and Notes
- •Thought Questions
- •The Fully Additive Model
- •Discounting in Continuous Time
- •Why Would Discounting Be Stable?
- •Naïve Hyperbolic Discounting
- •Naïve Quasi-Hyperbolic Discounting
- •The Common Difference Effect
- •The Absolute Magnitude Effect
- •History and Notes
- •References
- •Rationality and the Possibility of Committing
- •Commitment under Time Inconsistency
- •Choosing When to Do It
- •Of Sophisticates and Naïfs
- •Uncommitting
- •History and Notes
- •Thought Questions
- •Rationality and Altruism
- •Public Goods Provision and Altruistic Behavior
- •History and Notes
- •Thought Questions
- •Inequity Aversion
- •Holding Firms Accountable in a Competitive Marketplace
- •Fairness
- •Kindness Functions
- •Psychological Games
- •History and Notes
- •References
- •Of Trust and Trustworthiness
- •Trust in the Marketplace
- •Trust and Distrust
- •Reciprocity
- •History and Notes
- •References
- •Glossary
- •Index

|
|
|
|
|
432 |
|
FAIRNESS AND PSYCHOLOGICAL GAMES |
Kindness Functions
In this case we have defined kindness functions following a recipe suggested by Matthew Rabin—a rather complicated recipe. One way to index the fairness of a strategy is to compare it to the set of Pareto optimal outcomes. Recall that an outcome is Pareto optimal if no one can be made better off without making someone else worse off. In any non-Pareto optimum, someone can be made better off without making other players worse off. If this occurs it may be because someone has given up some of their own reward to give more to another (kindness) or because someone has given up some of their reward in order to hurt another (cruelty).
In the case of the Battle of the Sexes, there are two Pareto optimal allocations: (boxing, boxing) and (opera, opera). All other allocations strictly make everyone worse off. Examining the outcome (boxing, boxing), it would only be possible to make the wife better off by switching to the equilibrium (opera, opera), but this would result in making the husband worse off. When examining (opera, opera), it is possible to make the husband better off, but only by making the wife worse off. Thus, these are the two Pareto optimal outcomes. If the outcome is not a Pareto optimum, then it is possible to make one player better off without making either player worse off. In this case, one (or both) player(s) must be intentionally making the other worse off at the first player’s expense. For example, if we observe the outcome (boxing, opera), either player could make both players better off by switching their strategy.
Suppose Player 2 decides to play strategy b2. Then, the lowest amount the player would expect to obtain given Player 1 is being kind is the smallest possible Pareto optimal outcome given Player 2 employs b2. So, for example, if the wife decided to choose opera, then the lowest Pareto optimal payoff is 1. If the husband knows the wife will go to the opera, any payoff lower than 1 could only occur if the husband were being
cruel and lowering his own payout by 0.5 in order to reduce her payout by 1. Let πP b2
2
be the smallest Pareto optimal payoff that can be received by Player 2 given Player 2 employs strategy b2. Then, any result yielding a payout to Player 2 below πP2 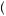 b2
b2 , given Player 2 follows b2, must result from Player 1 being cruel, leading to a negative value of the kindness function f1
, given Player 2 follows b2, must result from Player 1 being cruel, leading to a negative value of the kindness function f1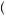 a1, b2
a1, b2 .
.
Alternatively, Player 2 will never receive more than the largest Pareto optimal payoff that can be received by Player 2 given Player 2 plays strategy b2 unless Player 1 is being kind. A higher payout could only be achieved by Player 1 intentionally giving up some of his payout in order for Player 1 to receive more. Let πP2 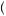 b2
b2 be the largest Pareto optimal outcome that can be received by Player 2 given Player 2 employs strategy b2. This must result from Player 1 giving up some material payoff in order to allow Player 2 a higher payout, resulting in a positive value of the kindness function, f1
be the largest Pareto optimal outcome that can be received by Player 2 given Player 2 employs strategy b2. This must result from Player 1 giving up some material payoff in order to allow Player 2 a higher payout, resulting in a positive value of the kindness function, f1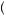 a1, b2
a1, b2 . Thus, Rabin proposes the kindness function
. Thus, Rabin proposes the kindness function
|
|
π2 a1, b2 − |
πP |
b2 + πP b2 |
|
|||
|
|
2 |
|
2 |
|
|
||
f1 a1, b2 |
= |
|
2 |
|
, |
15 14 |
||
π2P b2 |
− π |
2 b2 |
|
|||||
|
|
|
|
|
||||
where π2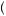 b2
b2 is the minimum possible payout (whether Pareto optimal or not) among all outcomes with Player 2 playing strategy b2. This function is negative if Player 2 receives
is the minimum possible payout (whether Pareto optimal or not) among all outcomes with Player 2 playing strategy b2. This function is negative if Player 2 receives

|
|
|
|
Kindness Functions |
|
433 |
|
less than the midpoint between the highest and lowest Pareto optimal amounts, and it is positive if Player 2 receives more than this amount.
This function leads directly to the kindness functions specified in equations 15.10 and 15.11. Consider the Battle of the Sexes from the wife’s point of view. The lowest Pareto
optimal amount the husband can receive if he chooses opera is πPHusband Opera
Opera = 0.5. The maximum Pareto optimal material payout given he chooses opera is
= 0.5. The maximum Pareto optimal material payout given he chooses opera is
πPHusband Opera
Opera = 0.5. The minimum amount overall that he can receive when choosing Opera is πHusband
= 0.5. The minimum amount overall that he can receive when choosing Opera is πHusband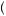 Opera
Opera = 0. Alternatively, if the husband chooses boxing, these values
= 0. Alternatively, if the husband chooses boxing, these values
are πPhusband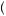 Boxing
Boxing = πPHusband
= πPHusband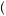 Boxing
Boxing = 1, πHusband
= 1, πHusband Boxing
Boxing = 0. Thus, the wife’s
= 0. Thus, the wife’s
kindness function is given by
|
0.5 − |
0.5 + 0.5 |
|
|
|
|||||||||
|
|
|
|
2 |
|
= 0 |
if |
aWife = Opera, bHusband = Opera |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
0.5 − |
0 |
|
|||||||||
|
|
|
|
|
|
|
||||||||
|
|
0 − |
0.5 + 0.5 |
|
|
|
|
|||||||
|
|
|
|
|
|
2 |
|
= − 1 |
if |
aWife = Boxing, bHusband = Opera |
||||
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
||||
fWife aWife, bHusband |
= |
|
0.5 − 0 |
|
|
. |
||||||||
|
− |
1 + |
1 |
|
|
|
|
|
||||||
|
0 |
|
|
|
|
|
|
|||||||
|
2 |
|
|
= − 1 |
if |
aWife = Opera, bHusband = Boxing |
||||||||
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
1 − 0 |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|||||
|
|
1 − |
1 + |
1 |
|
|
|
|
|
|
||||
|
|
2 |
|
|
= 0 |
|
if |
aWife = Boxing, bHusband = Boxing |
||||||
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
1 − 0 |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
15 15 |
Clearly, if the wife believes the husband is going to choose boxing and decides to choose opera in response, she is trying to be cruel, resulting in a value of −1. Similarly, if she believes he will choose opera and she decides to choose boxing in response, she is being cruel. Otherwise, she is giving him the best outcome he can achieve given his strategy— moreover she is doing so without any sacrifice of her own well-being. Thus, in either of the Pareto optimal outcomes, the kindness function value is 0.
Reciprocally, we can find the wife’s perceived kindness function, defining how kind she perceives her husband is being toward her. We define Player 1’s perception of the kindness of Player 2 as
|
|
|
|
|
π1 |
c1, |
b2 |
− |
π1P |
c1 + πP c1 |
|
|
|
|
|
|
|
|
2 |
|
|
||||
|
|
|
|
, c1 = |
|
|
|
|
|
1 |
|
|
|
|
f 2 |
b2 |
|
|
|
|
|
|
, |
15 16 |
|
|
|
|
π1P |
c1 |
− π |
c1 |
||||||
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
1 |
|
|
where the values π |
P |
c1 , π |
P |
c1 , and π |
1 c1 |
are defined as before, only now they rep- |
||||||
1 |
1 |
|||||||||||
resent the reward to Player 1 given Player 1 employs strategy c1. Recall that c1 is the strategy Player 1 believes that Player 2 believes Player 1 will employ. The lowest Pareto
optimal amount the Wife can receive if she plays Opera is πP Opera = 1. The
Wife
maximum Pareto optimal material payout given she plays Opera is πPWife Opera
Opera = 1.
= 1.

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
434 |
|
FAIRNESS AND PSYCHOLOGICAL GAMES |
|
|
|
|||||||||||||||
|
|
The |
minimum amount overall |
|
that she |
can |
receive when playing Opera is |
||||||||||||||
|
|
πWife |
Opera = 0. |
|
Alternatively, |
|
if the |
Wife |
plays Boxing, these values are |
||||||||||||
|
|
πP |
Boxing = πP |
|
Boxing |
= 0.5, π |
|
|
|
Boxing |
= 0. Thus, the Wife’s perception of |
||||||||||
|
|
|
Wife |
|
Wife |
|
|
|
|
|
|
|
|
|
Wife |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
the kindness of the husband is |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
1 − |
1 + |
1 |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
2 |
|
= 0 |
|
|
if |
cWife = Opera, bHusband = Opera |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
1 − 0 |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
0 − |
1 + |
1 |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
2 |
|
|
= − 1 |
if |
cWife = Boxing, bHusband = Opera |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
f Husband bHusband, |
cWife = |
1 − 0 |
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
, |
|||||||||||
|
|
− |
0.5 + 0.5 |
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
0 |
|
|
|
2 |
|
= |
− 1 |
if |
cWife = Opera, bHusband = Boxing |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
0.5 − 0 |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
0.5 − |
0.5 + 0.5 |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
= 0 |
if |
cWife = Boxing, bHusband = Boxing |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
0.5 − 0 |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
15 17 |
which is identical to the kindness function assumed in equation 15.11. As before, if the wife believes the husband thinks she will play opera, and he decides to play boxing in response, she believes he is behaving cruelly—hurting himself in order to hurt her. Alternatively, if the wife thinks the husband believes she will play boxing and he plays opera in response, she believes he is behaving cruelly. Both of these result in a value of −1. Alternatively, if she believes he is intending to coordinate with her to be at the same event, she believes he is not acting maliciously but maximizing both of their payouts. This results in a fairness value of 0.
There are many other candidate kindness functions that could be employed. The primary contribution of the fairness equilibrium is that people can behave very differently if they seek to reward the intent of their opponents rather than responding solely to the actions themselves. If intent is rewarded, cooperation can break down, leading to lower material payoffs for all. However, because the fairness equilibrium requires that all players have correct perceptions, it will always be the case that if any player is behaving kindly, both players behave kindly. Alternatively if any player is behaving cruelly, both players must behave cruelly or at best neutrally.
EXAMPLE 15.4 Rewarding Intent
Fairness provides one explanation for behavior in the ultimatum game. Consider an ultimatum game played between two players with kindness functions as proposed in the previous section. Suppose that the first player is given $10 to split between the two players, and the second player can either accept or reject. Given that this is a sequential game (Player 2 knows what Player 1’s strategy is by the time he makes any decisions), let us generalize the notion of a fairness equilibrium to a subgame perfect fairness

|
|
|
|
Kindness Functions |
|
435 |
|
equilibrium (which must constitute a fairness equilibrium in all subgames). In this case, a strategy by Player 1 will specify a proposed split of the cash between the two players. A strategy by Player 2 will specify which values will be accepted and which will not. For example, one reasonable strategy might specify that Player 2 would accept if he will receive more than $2.50 by doing so. Suppose that the first player offers a split in which Player 1 receives a1 and Player 2 receives 10 − a1. All possible splits are Pareto optimal. The only outcomes that are not Pareto optimal are those in which Player 2 rejects and both players receive $0.
Suppose that a2 is of the form reject if 10 − a1 < k and accept otherwise, where k is some constant between 0 and 10. The maximum Pareto optimal reward for Player 2 is thus πP2  a2
a2 = 10. The minimum Pareto optimal amount that could result from this strategy would be πP2
= 10. The minimum Pareto optimal amount that could result from this strategy would be πP2 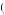 a2
a2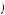 = k. Any offer that results in less than k would yield an outcome that is Pareto inefficient. The overall minimum reward is π2
= k. Any offer that results in less than k would yield an outcome that is Pareto inefficient. The overall minimum reward is π2 a2
a2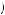 = 0. Thus, if a2 = b2 = c2, a1 = b1 = c1,
= 0. Thus, if a2 = b2 = c2, a1 = b1 = c1,
|
10 − a1 − |
10 + k |
|
1 |
|
|
|
a1 |
|
|
k |
|
|
||||||||
|
2 |
|
= |
− |
− |
− a1 |
≥ k |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
if 10 |
|||||||
|
|
|
|
|
|
2 |
10 |
|
|||||||||||||
f1 a1, b2 = f 1 b1, c2 |
= |
10 − 0 |
|
|
|
|
|
20 |
|
. |
|||||||||||
|
0 − |
10 + k |
|
|
1 |
|
|
|
k |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
2 |
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
= − |
|
− |
|
|
if 10 − a1 < k |
|||||||||||
|
|
|
10 − 0 |
2 |
20 |
||||||||||||||||
 15
15 18
18
Similarly, the maximum Pareto optimal reward for Player 1 given the proposed split of a1 is πP1  a1
a1 = a1. This is the amount Player 1 would receive if Player 2 accepted the offer no matter what it was. The minimum Pareto optimal amount that Player 1 could receive
= a1. This is the amount Player 1 would receive if Player 2 accepted the offer no matter what it was. The minimum Pareto optimal amount that Player 1 could receive
given a proposed split of a1 is also πP |
a1 = a1, because anything less must result from a |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|||
rejection of the offer. The overall minimum reward is π1 a1 = 0. Thus, if a2 = b2 = c2, |
|||||||||||||||||||||||
a1 = b1 = c1, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a1 − |
a1 + a1 |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
= 0 if 10 − a1 ≥ k |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
a1 − 0 |
|
|
||||||||
f2 a2, b1 = f 2 b2, c1 = 0 − |
a1 + a1 |
|
|
|
|
. |
15 19 |
||||||||||||||||
2 |
= − 1 if 10 − a1 < k |
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
a1 − 0 |
|
|||||||||
Thus, Player 2 must find the minimum amount he will accept, k, that solves |
|
||||||||||||||||||||||
maxk π2 a1, a2 + f 1 |
a1, a2 |
f2 a2, a1 |
|
|
|
|
|
||||||||||||||||
10 − a1 + |
|
1 |
− |
a1 |
|
− |
k |
× 0 = 10 − a1 |
if 10 − a1 ≥ k |
|
|||||||||||||
2 |
|
|
|
|
|||||||||||||||||||
|
10 |
|
20 |
|
|
|
|
|
|
|
|
|
|
15 20 |
|||||||||
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
0 − |
1 |
+ |
k |
|
− 1 = |
1 |
+ |
k |
|
if 10 − a1 < k |
|
||||||||||||
2 |
|
|
20 |
|
|||||||||||||||||||
|
|
20 |
|
|
|
|
|
|
2 |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
436 |
|
FAIRNESS AND PSYCHOLOGICAL GAMES |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
The value of this function is 10 − a1 |
for any value of k ≤ 10 − a1, and he will receive |
|||||||||||||||||||||||||||
|
|
1 2 + k 20 otherwise. The |
maximum value |
Player 2 can |
receive |
|
if he |
rejects is |
||||||||||||||||||||||
|
|
1 2 + 10 − a1 |
20, which will be received if the rejection point is set just above the |
|||||||||||||||||||||||||||
|
|
anticipated offer 10 − a1. Thus Player 2 will set k to some value lower than 10 − a1 if |
||||||||||||||||||||||||||||
|
|
10 − a1 > 1 2 + 10 − a1 |
|
20, which means the reward from accepting would be larger |
||||||||||||||||||||||||||
|
|
than the maximum possible reward from rejecting. Player 2 will be indifferent between |
||||||||||||||||||||||||||||
|
|
accepting and rejecting if |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
10 − a1 = |
1 |
+ |
|
10 − a1 |
, |
|
|
|
|
|
|
15 21 |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
20 |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|||
|
|
which implies that 10 − a1 = 10 19. For any value below this, Player 2 would be better off |
||||||||||||||||||||||||||||
|
|
rejecting. But for any value above this, Player 2 would be better off accepting. Therefore, |
||||||||||||||||||||||||||||
|
|
k = 10 19. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
We can now examine Player 1’s decision. In this case, f1 |
a1, b2 |
= f 1 |
a1, b2 , and |
||||||||||||||||||||||||
|
|
f 2 b2, c1 = f2 |
b2, c1 . Again, given that a2 = b2 = c2, a1 = b1 = c1, we can thus write Player |
|||||||||||||||||||||||||||
|
|
1’s strategy as solving |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
maxa1 π1 a1, |
a2 + f 2 |
a2, a1 |
|
f1 a1, a2 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
a1 + 0 × |
1 |
|
− |
|
a1 |
|
|
− |
|
1 |
|
= a1 |
if |
10 − a1 ≥ |
10 |
|
a1 ≤ |
|
180 |
|
|
||||||
|
|
2 |
|
|
|
|
|
|
19 |
|
19 |
|
|
|||||||||||||||||
|
|
|
|
|
|
10 |
|
38 |
|
|
|
|
|
|
|
|
|
|
15 22 |
|||||||||||
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
0 − − 1 × |
1 |
+ |
|
1 |
|
= |
20 |
|
|
if 10 − a1 < |
10 |
|
a1 > |
180 |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
2 |
|
38 |
38 |
|
|
19 |
|
19 |
|
|
||||||||||||||||||
|
|
Given this set of possible outcomes, and noting that 180 19 > 10 19, Player 1 will |
||||||||||||||||||||||||||||
|
|
choose the strategy in which Player 1 receives a1 = 180 19 |
9.47 and Player 2 receives |
|||||||||||||||||||||||||||
|
|
approximately 0.53. This split seems unfair, particularly for a fairness equilibrium. If |
||||||||||||||||||||||||||||
|
|
the kindness function were scaled up by multiplying each kindness function by |
||||||||||||||||||||||||||||
|
|
some factor greater than 1, the fairness equilibrium would display more evenly split |
||||||||||||||||||||||||||||
|
|
proposals in equilibrium. This could be achieved, for example, by writing the utility |
||||||||||||||||||||||||||||
|
|
functions in the form U1 a1, b2, c1 |
= π1 |
a1, b2 + ϕf 2 b2, c1 |
× f1 a1, b2 , |
where ϕ is |
||||||||||||||||||||||||
|
|
some number greater than 1. This implies that Player 2 will reject if k < ϕ |
2 − ϕ 10 . |
|||||||||||||||||||||||||||
|
|
Thus, if ϕ = 4, then Player 2 will reject if the offer yields less than $2.50 for Player 2, and |
||||||||||||||||||||||||||||
|
|
Player 1 will choose a split of $7.50 for Player 1 and $2.50 for Player 2, much like the |
||||||||||||||||||||||||||||
|
|
observed outcomes. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
The key notion of fairness is a desire to punish those who are cruel and reward those |
|||||||||||||||||||||||||||
|
|
who are kind. Kahneman, Knetsch, and Thaler conducted a series of experiments that |
||||||||||||||||||||||||||||
|
|
tested directly whether people wished to reward those who behave kindly and punish |
||||||||||||||||||||||||||||
|
|
those who behave cruelly. Their experiments were based on a variation of the dictator |
||||||||||||||||||||||||||||
|
|
game. The experiment took place in two phases. In the first phase, each player was made |
||||||||||||||||||||||||||||
|
|
a dictator and could choose between two possible allocations of money between |
||||||||||||||||||||||||||||
|
|
themselves and another anonymous player. In one allocation, the dictator would receive |
||||||||||||||||||||||||||||
|
|
$18 and the |
other |
player |
would receive $2. In the other |
allocation, |
both would |
|||||||||||||||||||||||

|
|
|
|
Kindness Functions |
|
437 |
|
receive $10. A total of 161 participants took part in this experiment, with 76 percent choosing an even split.
Next, in phase 2, players were randomly and anonymously paired with two other participants. They were told that one of the participants, whom we will call U for uneven, had played the role of dictator in the first round and taken $18, and the other participant, whom we will call E, had made an even split. The participant could then choose to share $12 with U, with both receiving $6, or to share $10 with E, with both receiving $5. The player in this second round did not know who either U or E were. Moreover, neither U nor E had made any decision that involved the decision maker. The uneven and even splits of money were all made with some other player who was now uninvolved in the game. Thus, strictly speaking, the definition of fairness given in the previous section should not apply. Any cruelty by U was directed elsewhere and should not affect the decision maker. We might thus expect people to take the larger reward by sharing with U. However, 74 percent decided to take the smaller reward and share with E.
Thus, it appears that decision makers are motivated not just to reward those who are kind to them and punish those who are cruel to them but also to reward those who are kind to others and punish those who are cruel to others. To consider this in the framework of the fairness model of utility, we could extend the basic model to include beliefs about how others have been treated by an opponent. Thus, a player in the second round could take U’s treatment of some other player as an indication that this player is cruel and E’s treatment of some other player as indicating that E is kind. In this case, the decision maker’s problem could be represented through a utility function that includes the fairness coefficients for both opponents involved:
U2 i = 6 + f 1 |
U f2 |
6 |
+ f 1 |
E f2 |
0 |
if |
i = U , |
15 23 |
5 + f 1 |
U f2 |
0 |
+ f 1 |
E f2 |
5 |
if |
i = E |
|
where f 1 i
i is negative if the opponent chose U in the first round, reflecting that the player was cruel, and f 1
is negative if the opponent chose U in the first round, reflecting that the player was cruel, and f 1 i
i is positive if the opponent chose E in the first round, reflecting that the player was kind. Alternatively, f2
is positive if the opponent chose E in the first round, reflecting that the player was kind. Alternatively, f2 0
0 ≤ 0 represents cruel (or at least neutral) treatment of the player who receives no material reward, and f2
≤ 0 represents cruel (or at least neutral) treatment of the player who receives no material reward, and f2 6
6 > f2
> f2 5
5 > 0 represents kind treatment of the player who receives a positive material reward. Thus, the player will choose E if
> 0 represents kind treatment of the player who receives a positive material reward. Thus, the player will choose E if
5 + f 1 U f2 0 + f 1 E f2 5 > 6 + f 1 U f2 6 + f 1 E f2 0 |
15 24 |
or |
|
f 1 U f2 0 − f2 6 + f 1 E f2 5 − f2 0 > 1. |
15 25 |
This would be the case if f 1 U
U was negative enough relative to f 1
was negative enough relative to f 1 E
E , reflecting a severe aversion to rewarding cruel behavior. The observed behavior in the experiment suggests that in the general population we would find such a strong aversion to helping out cruel people.
, reflecting a severe aversion to rewarding cruel behavior. The observed behavior in the experiment suggests that in the general population we would find such a strong aversion to helping out cruel people.

|
|
|
|
|
438 |
|
FAIRNESS AND PSYCHOLOGICAL GAMES |
EXAMPLE 15.5 For a Good Cause
Firms often advertise that they donate a portion of their profits for a specific cause. For example, several firms (ranging from beer bottling companies to Walmart) made a point of advertising their help in providing food and water to victims of Hurricane Katrina, which devastated the Gulf Coast in 2008. Such charitable giving might seem on the surface to be counterproductive to the goals of a profit-maximizing firm. If we assume, as economists do, that the firm’s only goal is to maximize profits, they should not be giving product or profit away. But, in reality, firm giving is pervasive.
One example may be instructive. A prominent yogurt brand, Yoplait, has an ongoing campaign in which they cap their yogurt containers in pink lids. They encourage their customers to collect the lids and redeem them online by typing in codes found on the lids. In return, for every lid redeemed, Yoplait promises to donate $0.10 toward breast cancer research and programs for those suffering or recovering from the disease. The lids are colored pink to draw attention to them and state that you can help fight breast cancer by visiting Yoplait’s website. If enough lids are redeemed, they promise to donate up to $2 million. This truly sounds like a firm being kind and helping others at a significant sacrifice of profits.
But then why would they ask customers to redeem the lids? It requires some effort and time to redeem the lids, which produces at least some cost. Moreover, it requires expenditure of money to administer the website and manage the dissemination and collection of lid codes. Previous incarnations of this program actually required customers to send the lids to the company through the mail. This required the customers to pay postage every time they sent in lids. In fact you would need to send in four lids before the donation to the cause would exceed the postage. If the company had set a goal to donate money out of their profits for the cause of breast cancer, they would not require such effort on the part of the customer because it reduces the amount donated. Rather, they could simply donate their $2 million plus whatever such efforts cost and possibly do more good. But doing so would eliminate the ability of the company to play upon the feelings of fairness their customers possess.
A large portion of yogurt consumers are women, and it is quite likely that a large portion of these customers feel strongly about breast cancer. Thus, donating some of the proceeds might help to win the loyalty of this customer base. However, to do so, you must find a powerful way to inform the customer base of your good deeds. In fact, Yoplait has made their donation directly proportional to the purchases of customers who are not only aware of the program but also feel strongly enough about breast cancer to take the time to redeem the lids. Not a single dime will go to breast cancer without first someone buying Yoplait yogurt and then, knowing about the good that Yoplait does, taking time to visit their website and enter in the codes on the lids. No money is wasted in building this reputation for kindness. In 1999 Yoplait promised to donate $0.50 per lid up to a maximum donation of only $100,000. But they received 9.4 million lids, which, but for the cap, would have resulted in a donation of $4.7 million. This nearly resulted in a lawsuit when the state of Georgia began to investigate the program. Make no mistake, corporate philanthropy is very carefully calculated and limited.
Kindness has many applications in the business world, from human resources to customer relations. For example, one much-publicized study has found that doctors who

|
|
|
|
Kindness Functions |
|
439 |
|
are at fault for a medical error face fewer lawsuits and lower costs if they simply apologize. In the context of the kindness model, doctors who appear to be at fault but are unwilling to admit it look as if they will not admit the error simply to avoid paying for damages. This type of treatment can be interpreted as cruel by the harmed patient, who might then wish to inflict financial pain on the doctor, even at the patient’s own expense, by filing a lawsuit. The doctor who apologizes legally admits fault and thus would be responsible for any damages should the case go to court. But seeing that the doctor opened himself up to such a possibility of legal claims might remove the patient’s desire to sue. At that point, the patient no longer wants to inflict pain on the errant doctor. Kindness pays.
EXAMPLE 15.6 Fairness, Wages, and Teams
One puzzle that has perplexed economists is the lack of detail in most labor contracts. Often a contract states nothing more than a per-hour wage and the possibility of being fired for any reason. Economic theory suggests that if possible, the employer and the laborer would both like to specify a contract that outlined the circumstances that would result in bonuses or raises as well as deductions to wages for poor performance. An employer should like to be able to go so far as to specify the attitude of the employees, presumably instructing them to be cooperative, compliant, and upbeat. Without more included in the contract, what prevents workers from shirking their duty substantially or even making themselves something of a nuisance to others in the workplace so long as they continue to provide some positive value? Employers really don’t have the ability to observe everything the worker does, or their attitude toward their work, which should lead to substantial shirking. In this case, however, it may be effective to rely on the worker’s sense of fairness to incline the worker toward a better attitude and a higher level of effort.
Ernst Fehr, Simon Gächter, and Georg Kirchsteiger used a series of experiments to see if someone in the employer’s position could use fairness to elicit higher effort from their employees. This laboratory experiment paired people in the role of employee and employer. Employers could select a wage, w, and a desired effort level, e, where 1 ≤ e ≤ 10, for their employees. There were six employers who made such decisions and eight workers who could decide to accept any of the contracts. However, only one worker could be employed by any employer, and thus there was an excess of labor in this market. The employee who accepted the contract could decide on any level of effort he desired, e, where 1 ≤ e ≤ 10, even if that level were below that desired by their employer, and would receive w irrespective of their effort level. The employer would then earn π = 10e − w, and the worker would receive u = w − c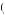 e
e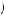 , where c
, where c e
e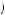 was a positive and increasing function of effort.
was a positive and increasing function of effort.
In this case, a purely selfish employee should behave so as to solve
maxe w − c e |
15 26 |
and because w does not depend on e, and because the cost of e is positive, the worker should choose the minimum possible effort, e = 1, no matter what the wage. Knowing

|
|
|
|
|
|
440 |
|
FAIRNESS AND PSYCHOLOGICAL GAMES |
|
|
|
this, the selfish employer should offer the lowest wage possible that ensures that a |
||
|
|
worker will take the contract: |
|
|
|
|
|
maxw π = 10e − w = 10 × 1 − w |
15 27 |
|
|
subject to |
|
|
|
|
|
w > c 1 . |
15 28 |
This will be solved where w = c 1
1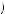 . Note that the desired level of effort doesn’t play any role in either decision and is thus irrelevant in the standard SPNE. Instead, no matter what desired effort level is specified, the result should be low wages and low-effort employees.
. Note that the desired level of effort doesn’t play any role in either decision and is thus irrelevant in the standard SPNE. Instead, no matter what desired effort level is specified, the result should be low wages and low-effort employees.
Instead, suppose that the employee displayed fairness preferences. In this case, the employee’s problem would be given by
maxew − c e + f employer w, e e* w, e × femployee e w, e |
15 29 |
where e*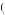 w, e
w, e is what the employee believes the employer will believe the optimal fairness strategy of the employee is, and e is the employer’s desired level of effort. If the wage offered relative to the desired effort level is high, then employees would expect to reap a large profit even if they didn’t put in the effort requested. This could lead to employees assigning positive value to f employer , because the employer is subjecting himself to possible losses in order to benefit the employee.
is what the employee believes the employer will believe the optimal fairness strategy of the employee is, and e is the employer’s desired level of effort. If the wage offered relative to the desired effort level is high, then employees would expect to reap a large profit even if they didn’t put in the effort requested. This could lead to employees assigning positive value to f employer , because the employer is subjecting himself to possible losses in order to benefit the employee.
Suppose for example that f employer = k1 × 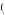 w − c
w − c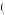 e
e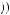 . In turn, employees might then feel bad if they deliver less than the level of effort desired, reflected in a negative value for femployee if e < e, with the value becoming more negative the less effort is put in. For example, suppose that femployee = k2 ×
. In turn, employees might then feel bad if they deliver less than the level of effort desired, reflected in a negative value for femployee if e < e, with the value becoming more negative the less effort is put in. For example, suppose that femployee = k2 ×  e − e
e − e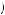 . This turns the last term of equation 15.29 to be increasing in effort, potentially leading the employee to provide much more effort than the minimum requested. Given the two example functions we have specified, the employee would solve
. This turns the last term of equation 15.29 to be increasing in effort, potentially leading the employee to provide much more effort than the minimum requested. Given the two example functions we have specified, the employee would solve
maxew − c e + k1k2 w − c e e − e . |
15 30 |
Now the marginal cost of effort remains the slope of the c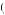 e
e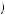 curve, represented by c’
curve, represented by c’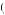 e
e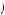 , but there is now also a benefit to effort if w > c
, but there is now also a benefit to effort if w > c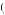 e
e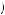 given by the third term. The marginal benefit in this case is k1k2
given by the third term. The marginal benefit in this case is k1k2 w − c
w − c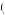 e
e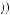 . Thus, the worker would provide effort such that marginal benefit of effort equals marginal cost of effort, c’
. Thus, the worker would provide effort such that marginal benefit of effort equals marginal cost of effort, c’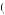 e
e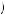 = k1k2
= k1k2 w − c
w − c e
e , as depicted in Figure 15.4. If the marginal cost of effort is increasing in the level of effort, this suggests that the level of effort would be increasing in wage and decreasing in desired effort level. The employers should respond to this by offering a wage that is high relative to the level of effort desired.
, as depicted in Figure 15.4. If the marginal cost of effort is increasing in the level of effort, this suggests that the level of effort would be increasing in wage and decreasing in desired effort level. The employers should respond to this by offering a wage that is high relative to the level of effort desired.
In fact, the average effort level observed was 4.4, well above the level of 1 that would be predicted by the selfish model. Additionally, employers offered relatively generous wages. If employees had worked the average desired effort level stated in the contract, which was e = 7, they would have taken just under half of the surplus, only a little less than the employers. Their actual take was more than half, however, because employees gave somewhat less effort than the contract had requested. While employees shirked, they did

|
|
|
|
Kindness Functions |
|
441 |
|
$
c'(e)
k1k2 (w – c(ê))(e – ê)
c'(e*)
|
|
FIGURE 15.4 |
|
|
Fairness and Effort Level in Labor Con- |
e* |
e |
tracts |
perform better than they would have had they been selfish, and employers received more profit than if they had offered the minimum wage for a minimum level of effort.
Fairness might not only be a reason for relatively high wages in the marketplace; it might also be a reason for the use of teams in contract labor. Standard economic theory suggests that teams may be a particularly bad idea for managing work. If people are purely selfish, then working in a team can offer an opportunity to hide the fact that they are putting in a very low effort. We have all had experience with group assignments in a class in which one of the members does very little work but receives the same grade as the rest of the team. This is an illustration of what happens when people are selfish. If all people are selfish, managers should avoid teams. However, if they must use teams, then the manager would need to impose severe team-wide penalties for low performance to align the individual member’s incentives with the manager’s own desires. In this case, all would be punished for the sins of any one shirker.
Instead, if team members act according to fairness, such steep incentives might not be necessary. In fact, in some circumstances, fairness can lead teams to be more efficient than each employee is in individual labor assignments. If team members observe others in the team making sacrifices for the good of the team, feelings of fairness can drive the rest to similar behavior. This could lead to strong motivations for each individual employee to perform well above the level that could be enforced by an individual labor contract. Alternatively, team members who observe others shirking could go into punishment mode, with efforts devolving into a cutthroat and unproductive mess.
Firms use teams for many functions: product design, implementation, and marketing. The firms that design and create some of the most successful products in the world are designed in teams. Firms like Apple seem to elicit from their employees work that goes well beyond the response to the basic incentives their job would provide. Workers describe being involved in something extraordinary and transcendent. When people feel this way they tend to cooperate and act in a way that rewards the efforts of others around them. Understanding fairness and the basics of human relationships is essential to effectively managing workers.

|
|
|
|
|
442 |
|
FAIRNESS AND PSYCHOLOGICAL GAMES |
EXAMPLE 15.7 Punishing for the Greater Good
The provision of public goods is of central interest to many economists. As discussed in prior chapters, if everyone benefits from the provision of a good, people will not want to contribute their private funds for the benefit of all and may instead decide to rely on others to contribute. Across the United States, on July 4 thousands of small communities put on a public fireworks display to celebrate the anniversary of the signing of the Declaration of Independence. These displays are often very costly, yet they often rely on voluntary contributions of the townspeople. A fireworks display usually can be seen for miles around, making it impossible to charge everyone who enjoys the display an admission fee. Instead, the plea goes out for contributions to the annual fireworks fund.
Consider a small town with just one truly wealthy family and many with much more modest means. Each year the wealthy family could foot the bill, but it likes to see the other families contribute. The wealthy family behaves so as to reward kindness and to punish cruelty. When they see others contributing to the effort, even if it is a relatively small amount, they consider this a kind gesture and like to reward this effort by making up the difference necessary to provide a satisfying show. When many of the townsfolk don’t contribute, but rather decide to take a free ride off the contributions of others, the wealthy family perceives this as a cruel act and wishes to punish it. But therein lies the problem. There is no direct way to punish a single free rider. Instead, the only punishment available is to eliminate their contribution to the fireworks display, eliminating the possibility of a display for that year. Such a punishment would punish not only the free riders but also everyone else in the town. In this case, if there are enough selfish people in the town who decide to free ride, the wealthy family—though behaving only so as to reward others for their behavior—could end up behaving as if they were selfish by eliminating their own contribution.
In general, those who desire fairness may decide to free ride if they want to punish other free riders. This could lead to underprovision of public goods even if there are only a relatively small number of selfish actors. Ernst Fehr and Simon Gächter found this behavior in a simple experiment where four people were each given 20 tokens. They could keep these tokens or contribute some amount of them to a public good yielding each member of the group 0.4 tokens. By keeping all of their tokens, they would be strictly better off, but if all gave all of their tokens to the public good, each would walk away with a total of 32 tokens, much better than the 20 they would otherwise walk away with. However, if people are given the option to provide punishment to an individual rather than the group, suddenly one can induce the selfish players to behave as if they are kind. In the case of their experiment, any player could strip one other player of tokens by paying 1/3 of a token for each token eliminated from the other player’s purse. When players are given the option to punish a single bad apple, selfish individuals realize they stand to lose if they are singled out for punishment by the rest. In this case, it is now in their self-interest to give for the public good. In this case, the way punishment is administered can play a big role in whether or not a public good will be provided.
Game theorists have noted the importance of being able to punish other players in obtaining better outcomes for all. One of the most important theorems in all of game theory deals with games that are repeated over and over again for an infinite number of periods (or at least players don’t know when the game will end, so it is treated as an
