
- •Brief Contents
- •Contents
- •Preface
- •Who Should Use this Book
- •Philosophy
- •A Short Word on Experiments
- •Acknowledgments
- •Rational Choice Theory and Rational Modeling
- •Rationality and Demand Curves
- •Bounded Rationality and Model Types
- •References
- •Rational Choice with Fixed and Marginal Costs
- •Fixed versus Sunk Costs
- •The Sunk Cost Fallacy
- •Theory and Reactions to Sunk Cost
- •History and Notes
- •Rational Explanations for the Sunk Cost Fallacy
- •Transaction Utility and Flat-Rate Bias
- •Procedural Explanations for Flat-Rate Bias
- •Rational Explanations for Flat-Rate Bias
- •History and Notes
- •Theory and Reference-Dependent Preferences
- •Rational Choice with Income from Varying Sources
- •The Theory of Mental Accounting
- •Budgeting and Consumption Bundles
- •Accounts, Integrating, or Segregating
- •Payment Decoupling, Prepurchase, and Credit Card Purchases
- •Investments and Opening and Closing Accounts
- •Reference Points and Indifference Curves
- •Rational Choice, Temptation and Gifts versus Cash
- •Budgets, Accounts, Temptation, and Gifts
- •Rational Choice over Time
- •References
- •Rational Choice and Default Options
- •Rational Explanations of the Status Quo Bias
- •History and Notes
- •Reference Points, Indifference Curves, and the Consumer Problem
- •An Evolutionary Explanation for Loss Aversion
- •Rational Choice and Getting and Giving Up Goods
- •Loss Aversion and the Endowment Effect
- •Rational Explanations for the Endowment Effect
- •History and Notes
- •Thought Questions
- •Rational Bidding in Auctions
- •Procedural Explanations for Overbidding
- •Levels of Rationality
- •Bidding Heuristics and Transparency
- •Rational Bidding under Dutch and First-Price Auctions
- •History and Notes
- •Rational Prices in English, Dutch, and First-Price Auctions
- •Auction with Uncertainty
- •Rational Bidding under Uncertainty
- •History and Notes
- •References
- •Multiple Rational Choice with Certainty and Uncertainty
- •The Portfolio Problem
- •Narrow versus Broad Bracketing
- •Bracketing the Portfolio Problem
- •More than the Sum of Its Parts
- •The Utility Function and Risk Aversion
- •Bracketing and Variety
- •Rational Bracketing for Variety
- •Changing Preferences, Adding Up, and Choice Bracketing
- •Addiction and Melioration
- •Narrow Bracketing and Motivation
- •Behavioral Bracketing
- •History and Notes
- •Rational Explanations for Bracketing Behavior
- •Statistical Inference and Information
- •Calibration Exercises
- •Representativeness
- •Conjunction Bias
- •The Law of Small Numbers
- •Conservatism versus Representativeness
- •Availability Heuristic
- •Bias, Bigotry, and Availability
- •History and Notes
- •References
- •Rational Information Search
- •Risk Aversion and Production
- •Self-Serving Bias
- •Is Bad Information Bad?
- •History and Notes
- •Thought Questions
- •Rational Decision under Risk
- •Independence and Rational Decision under Risk
- •Allowing Violations of Independence
- •The Shape of Indifference Curves
- •Evidence on the Shape of Probability Weights
- •Probability Weights without Preferences for the Inferior
- •History and Notes
- •Thought Questions
- •Risk Aversion, Risk Loving, and Loss Aversion
- •Prospect Theory
- •Prospect Theory and Indifference Curves
- •Does Prospect Theory Solve the Whole Problem?
- •Prospect Theory and Risk Aversion in Small Gambles
- •History and Notes
- •References
- •The Standard Models of Intertemporal Choice
- •Making Decisions for Our Future Self
- •Projection Bias and Addiction
- •The Role of Emotions and Visceral Factors in Choice
- •Modeling the Hot–Cold Empathy Gap
- •Hindsight Bias and the Curse of Knowledge
- •History and Notes
- •Thought Questions
- •The Fully Additive Model
- •Discounting in Continuous Time
- •Why Would Discounting Be Stable?
- •Naïve Hyperbolic Discounting
- •Naïve Quasi-Hyperbolic Discounting
- •The Common Difference Effect
- •The Absolute Magnitude Effect
- •History and Notes
- •References
- •Rationality and the Possibility of Committing
- •Commitment under Time Inconsistency
- •Choosing When to Do It
- •Of Sophisticates and Naïfs
- •Uncommitting
- •History and Notes
- •Thought Questions
- •Rationality and Altruism
- •Public Goods Provision and Altruistic Behavior
- •History and Notes
- •Thought Questions
- •Inequity Aversion
- •Holding Firms Accountable in a Competitive Marketplace
- •Fairness
- •Kindness Functions
- •Psychological Games
- •History and Notes
- •References
- •Of Trust and Trustworthiness
- •Trust in the Marketplace
- •Trust and Distrust
- •Reciprocity
- •History and Notes
- •References
- •Glossary
- •Index

|
|
|
|
|
368 |
|
COMMITTING AND UNCOMMITTING |
earlier than the naïf but after the time-consistent decision maker. Thus, the sophisticate does not realize the utility he could if he completed the task earlier, but he is better off than the naïf in this case. Alternatively, proposition 13.4 tells us with an immediate reward, the sophisticate completes the task even earlier than the naïf, leading potentially to an even severer loss of welfare. Thus, the sophisticate may be worse off owing to his misperception of how he will discount utility in the future and his awareness of how this perception of discounting will lead him to behave in future periods. Sophisticates might correctly perceive how they will behave in the future, but they still misperceive the value of future rewards and costs. The welfare penalty to being a sophisticate in immediatereward activities depends heavily on the assumption that sophisticates undervalue future rewards, because β < δ, though they anticipate the decisions they will make in the future.
Of Sophisticates and Naïfs
Although the dichotomy of sophisticates and naïfs is appealing, it seems unrealistic. In our own personal experience with the world, we can find examples where we anticipate that we will procrastinate, but might not realize the extent to which we will procrastinate. When undesirable outcomes occur, instead of saying, “I knew I would do this,” we might instead say “I knew I would procrastinate, but I never imagined it would go so far.”
O’Donoghue and Rabin propose modeling a form of partial naïfs. A partial naïf anticipates that he will make decisions in the future based upon quasi-hyperbolic discounting with a parameter β, but he actually behaves as a quasi-hyperbolic discounter with parameter β for any current-period decision. The parameter β represents the person’s perception of future discounting and is such that β ≤ β ≤ δ. Thus, the decision maker always perceives that he is closer to having time-consistent preferences than he truly is. This model allows people to be trapped by temptation owing to their misperception of future discounting, at the same time still taking precautions to avoid such traps.
Consider the student who must choose when to study for a test that will take place in three days. Let us suppose that the cost of studying will be the same no matter which of the three days he studies, but studying earlier will provide a greater benefit. Specifically, suppose that v = 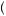 15, 12, 7
15, 12, 7 and c =
and c =  8, 8, 8
8, 8, 8 , and that studying is an immediate-cost activity. For simplicity, suppose that δ = 1. Then, the partial naïf believes he will behave like a sophisticate with parameter β but will actually behave according to β. Let us suppose that β = 1
, and that studying is an immediate-cost activity. For simplicity, suppose that δ = 1. Then, the partial naïf believes he will behave like a sophisticate with parameter β but will actually behave according to β. Let us suppose that β = 1 2.
2.
To solve for how partial naïfs behave in the first period, we can solve by backward induction. In the second period, partial naïfs believe that they will either study in that
period |
and |
obtain u = 12β − 8 or postpone to the last period and receive |
||
u = β |
7 − |
8 |
= − β. Thus partial naïfs would anticipate choosing period 2 over period 3 if |
|
β > 8 |
|
13. |
Suppose this is the case. Then the partial naïfs believe they will choose to |
|
study in period 2 rather than 3. In evaluating the decision in the first period, however, they employ their actual parameter β. Thus, they choose between studying now and obtaining u = 15β − 8 = − 0.5, or studying the next day and obtaining u = β 12 − 8
12 − 8 = 2.
= 2.

|
|
|
|
Of Sophisticates and Naïfs |
|
369 |
|
Thus, partial naïfs decide to postpone studying until the second day, believing that they will have the willpower to study on the second day. But when they actually arrive at the second day, they now decide between the second and third day using the actual parameter β = 1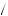 2. Thus, they choose either to study in that period and obtain u = β12 − 8 = − 2, or study on the third day and obtain u = β
2. Thus, they choose either to study in that period and obtain u = β12 − 8 = − 2, or study on the third day and obtain u = β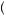 7 − 8
7 − 8 = − 1
= − 1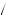 2. Thus, partial naïfs decide to postpone until the last day even though they had planned to complete the studying in the second day. You can use backward induction to confirm that in this case, if β = β = 1
2. Thus, partial naïfs decide to postpone until the last day even though they had planned to complete the studying in the second day. You can use backward induction to confirm that in this case, if β = β = 1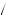 2, the sophisticate would have studied the first day instead.
2, the sophisticate would have studied the first day instead.
 EXAMPLE 13.3 Gym Membership and Incentives
EXAMPLE 13.3 Gym Membership and Incentives
Gyms often offer several membership plans, including automatic monthly fees that allow you to visit the gym as often as you like, or a fee for each visit. Usually the monthly fees equal the cost of going to the gym several times at the individual visit price. Obviously, those who anticipate going to the gym often will benefit from a monthly fee relative to the fee-for-visit plan. Alternatively, those who anticipate not going very often could save money by just paying for the few times they do visit. As mentioned in Chapter 2, gym patrons in many cases behave in ways that do not make much sense. Stefano DellaVigna and Ulrike Malmendier found that at a group of three gyms, monthly membership fees of $70 allow members to visit as often as they like, whereas members without the monthly membership can buy a 10-visit pass for $100. Thus, members should only buy the monthly membership if they anticipate attending the gym more than seven times per month on average. Otherwise, they could buy the 10-visit pass for an average cost of $10 per visit. But instead of more than seven visits per month, the average member who pays the monthly fee attends only 4.3 times a month. This is clearly not consistent with rational preferences. But what could explain it?
Several other findings might help shed light on the behavior. Through a survey administered at a local mall, DellaVigna and Malmandier found that people attend the gym about half as often as they plan to. Survey respondents were asked how many times they planned to attend the gym in a particular month. These responses were then compared to actual attendance frequencies. This is consistent with naïve decision making, because people are not able to carry out the plans that they anticipate. Second, they found that people who stop going to the gym altogether tend to wait an average of 2.3 months (a cost of $187) before cancelling the gym membership. Whereas sophisticates would know to cancel their gym membership when they would no longer attend, a naïf would not necessarily cancel the gym membership, believing they would attend in the future. In fact, the evidence points to gym members who are at least partial naïfs. The authors calibrate a model of naïve gym membership that closely predicts all of the observed behavior, with daily discount factors of δ = 0.9995, and β = 0.7. Thus, although it is possible to find examples of commitment mechanisms suggesting sophistication, there is also substantial evidence of naïve behavior.
|
|
|
|
|
|
370 |
|
COMMITTING AND UNCOMMITTING |
|
|
|
|
|
|
|
|
|
EXAMPLE 13.4 |
Choosing What and When |
|
|
|
|
|
Jess has just come into $11,000, and wants to find a good strategy for investing the money. In perusing the investment options, he discovers that the number and types of investments available are overwhelming. He knows it will take significant work to determine the best investment strategy. Thus, he decides to put $10,000 in a savings account that earns nearly zero interest for now and put $1,000 in a simple mutual fund designed to mirror a general stock index. The stock index fund returns about 5 percent per year but can be risky. He resolves to invest the necessary time to determine the best place to put his money in the future. In the future, however, he never seems to find the time, and after three years he has not yet invested the $10,000. The $1,000 however, increases in value in the same time to about $1,160. Had he invested the rest at the same time, he could have made a substantially greater return. Often people put off doing what is best in favor of doing what is good. Ted O’Donoghue and Matthew Rabin point to the role of time-inconsistent preferences in these seemingly misplaced priorities.
Consider an infinite-horizon decision problem in which Kerry has two actions available to him, x1 and x2. These actions might represent investment options or other tasks that induce an immediate cost but accrue benefits into futurity—forever. Each action can only be completed at one point in time, and if you complete one of these tasks you cannot complete the other task at any point in time. For example, you cannot invest all of your money in the stock market and invest all of your money in a bank account. Suppose that taking any action xi, i = 1, 2 will result in an immediate cost of ci ≥ 0 and then a benefit of vi ≥ 0 that is given to Kerry each period thereafter. Let x0 represent the action of not completing any task, with c0 = 0, v0 = 0. A time-consistent decision maker will decide on which activity to complete by maximizing his discounted utility. Thus, in any period in which Kerry has not yet completed the task, t, he must choose a time period  t
t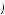 and an activity
and an activity  i
i , solving
, solving
maxi 0,1,2 − δt ci + |
δt vi = δt |
δ |
vi − ci |
, |
13 67 |
|
|
||||||
1 − δ |
||||||
t ≥ 0 |
t = t + 1 |
|
|
|
where the last equality follows from the properties of geometric series.1 Note that for any i such that δvi 1 − δ
1 − δ − ci > 0, Kerry would decide to complete the task now (at t = 0), because δ0 = 1 > δt for any t > 0, deriving greater benefit from doing it now. Thus timeconsistent decision makers always choose the task that maximizes δvi
− ci > 0, Kerry would decide to complete the task now (at t = 0), because δ0 = 1 > δt for any t > 0, deriving greater benefit from doing it now. Thus timeconsistent decision makers always choose the task that maximizes δvi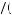 1 − δ
1 − δ − ci and perform the task immediately.
− ci and perform the task immediately.
Now, suppose instead that Kerry is partially naïve, with parameter β < β ≤ 1. The decision maker always faces exactly the same decision in any time period that is reached. The payouts to different activities only depend on what period an action is taken, and these payouts are fixed. Thus, if Kerry’s preferences and perceptions lead him to postpone until period 2, he would also decide to postpone until period 3, and so on, forever.
1 Let Y = krt + krt + 1 + |
= t = 0 krt , where 0 < r < 1. Then Y = krt 1 − r . To see |
this, note that |
Y = krt + krt + 1 + krt + 2 + |
. Also, rY = krt + 1 + krt + 2 + krt + 3 + . Thus, Y − rY = krt , or Y 1 − r |
= krt , implying |
the result. In this case, k = vi, and r = δ.
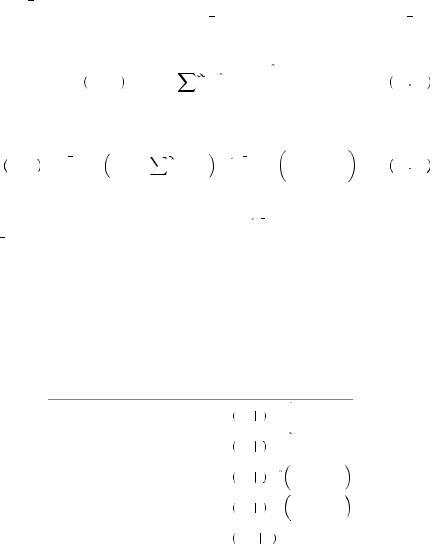
|
|
|
|
Of Sophisticates and Naïfs |
|
371 |
|
However, if Kerry recognizes that such procrastination will occur, he will instead decide to act now.
Let u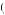 i, t
i, t t′
t′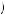 be the utility function Kerry in period 1 believes he will face when entering period t′ from taking action i at time t. In period t′, if the action is taken at t = t′ Kerry will perceive a utility function
be the utility function Kerry in period 1 believes he will face when entering period t′ from taking action i at time t. In period t′, if the action is taken at t = t′ Kerry will perceive a utility function
|
|
u i, t′ t′ = − ci + |
|
t = 0 βδt vi = |
|
β |
vi − ci. |
|
13 68 |
||||
|
|
|
|
|
|||||||||
|
1 − δ |
|
|||||||||||
If the action is taken later, Kerry at period 1 believes he will perceive in period t′ |
|||||||||||||
|
|
′ |
|
|
|
′ |
|
δ |
|
|
|
||
|
|
|
|
|
|
|
|
|
|||||
u i, t t′ = βδt − t |
− 1 − ci + |
|
|
δt vi = βδt − t |
− 1 |
|
vi |
− ci . |
13 69 |
||||
t |
= 1 |
1 − δ |
|||||||||||
|
|
|
|
|
|
|
|
|
|
||||
Note that in both cases, if δvi 1 − δ
1 − δ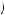 − ci > 0, Kerry would never choose to postpone the activity more than 1 period beyond t′. This is because βδt − t′ − 1
− ci > 0, Kerry would never choose to postpone the activity more than 1 period beyond t′. This is because βδt − t′ − 1 δvi
δvi 1 − δ
1 − δ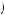 − ci
− ci is greatest when t = t′. Note that this is Kerry’s perception in period 1 considering a generic period in the future, t′. Because Kerry would never delay more than one period beyond the next, if he considers what he would do if he postponed executing an activity until period 2, he believes only one of five things could happen: execute x1 in period 2, execute x2 in period 2, execute x1 in period 3, execute x2 in period 3, do nothing in either.
is greatest when t = t′. Note that this is Kerry’s perception in period 1 considering a generic period in the future, t′. Because Kerry would never delay more than one period beyond the next, if he considers what he would do if he postponed executing an activity until period 2, he believes only one of five things could happen: execute x1 in period 2, execute x2 in period 2, execute x1 in period 3, execute x2 in period 3, do nothing in either.
Kerry anticipates that he will compare the discounted utility from the point of view of a period 2 decision maker for each of these options, choosing the option that yields the greatest utility:
Execute x1 |
|
u 1, 2 2 |
= |
|
|
β |
− c1 |
|||
in period 2: |
|
|
|
v1 |
||||||
|
1 − δ |
|||||||||
Execute x2 |
|
u 2, 2 2 |
= |
|
|
β |
− c2 |
|||
in period 2: |
|
|
|
v2 |
||||||
|
1 − δ |
|||||||||
Execute x1 |
in period 3: |
u 1, 3 2 |
= |
β |
|
δ |
v1 |
− c1 |
||
|
|
|||||||||
|
1 − δ |
|||||||||
Execute x2 |
in period 3: |
u 2, 3 2 |
= |
β |
|
δ |
v2 |
− c2 |
||
|
|
|||||||||
|
1 − δ |
|||||||||
Do nothing |
u 0, − − = 0 |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
If either u 1, 2
1, 2 2
2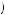 or u
or u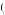 2, 2
2, 2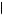 2
2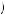 is the greatest of these five options, then in the first period Kerry decides on whether executing either x1 or x2 in period 1 would yield more utility (as perceived in period 1) than the corresponding action in period 2.
is the greatest of these five options, then in the first period Kerry decides on whether executing either x1 or x2 in period 1 would yield more utility (as perceived in period 1) than the corresponding action in period 2.
Suppose action xi in period 2 is the greatest of the five, and thus Kerry anticipates completing action xi. Then in period 1, he contemplates the utility (from the perspective of the period 1 decision maker) of the three options: execute x1 in period 1, execute x2 in period 1, execute xi in period 2. The corresponding utilities are given by

|
|
|
|
|
|
|
|
|
|
|
|
|
372 |
|
COMMITTING AND UNCOMMITTING |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Execute x1 |
|
u 1, 1 1 |
= |
β |
− c1 |
|
|
|
|
|
|
in period 1: |
|
v1 |
|
||||
|
|
|
|
1 − δ |
|
||||||
|
|
|
|
Execute x2 |
|
u 2, 1 1 |
= |
β |
− c2 |
|
|
|
|
|
|
in period 1: |
|
v2 |
|
||||
|
|
|
|
1 − δ |
|
||||||
|
|
|
|
Execute xi |
in period 2: |
u i, 2 1 |
= β 1 −δ δ vi − ci |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
Kerry would then choose the best of these options. However, if choosing to perform xi in period 2 is the best option, Kerry will put off the decision until period 2. But, once entering period 2, he faces a decision problem identical to that faced in period 1. Now Kerry discounts period 3 according to β but believes once entering period 3 he will discount period 4 according to β. In this case, equations 13.68 and 13.69 represent from the point of view of period 2 the utility that will be perceived by a period 3 decision maker contemplating executing in period 3 or later. In this case Kerry would then make the same decision to procrastinate. Similarly, Kerry would procrastinate endlessly— always planning to perform xi in the next period but never actually executing.
Alternatively, if u 1, 3
1, 3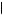 2
2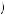 or u
or u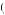 2, 3
2, 3 2
2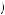 yields the greatest utility of the five options available when evaluating the anticipated second-period decision (thus either executing x1 in period 3 or x2 in period 3 are anticipated to be perceived the best choices in period 2), then the anticipated third-period decision maker would also decide to postpone or procrastinate. To see this, consider the third-period decision from the point of view of the first-period decision maker. The possible choices are again execute x1 in period 3, execute x2 in period 3, execute x1 in period 4, execute x2 in period 4, do nothing in either. The decision maker in period 1 believes that he will perceive the following utilities in period 3:
yields the greatest utility of the five options available when evaluating the anticipated second-period decision (thus either executing x1 in period 3 or x2 in period 3 are anticipated to be perceived the best choices in period 2), then the anticipated third-period decision maker would also decide to postpone or procrastinate. To see this, consider the third-period decision from the point of view of the first-period decision maker. The possible choices are again execute x1 in period 3, execute x2 in period 3, execute x1 in period 4, execute x2 in period 4, do nothing in either. The decision maker in period 1 believes that he will perceive the following utilities in period 3:
Execute x1 |
|
u 1, 3 3 |
= |
|
|
β |
− c1 |
|
in period 3: |
|
|
v1 |
|||||
|
1 − δ |
|||||||
Execute x2 |
|
u 2, 3 3 |
= |
|
|
β |
− c2 |
|
in period 3: |
|
|
v2 |
|||||
|
1 − δ |
|||||||
|
|
|
|
|
|
δ |
|
|
Execute x1 |
in period 4: |
u 1, 4 3 |
= |
β |
1 − δ v1 − c1 |
|||
|
|
|
|
|
|
δ |
|
|
Execute x2 |
in period 4: |
u 2, 4 3 |
= |
β |
1 − δ v2 − c2 |
|||
Do nothing |
u 0, − − = 0 |
|
||||||
|
|
|
|
|
|
|
|
|
These are identical to the options thought to be perceived by a second-period decision maker. Thus Kerry will again choose to postpone to period 4. Because the firstperiod decision maker recognizes this infinite procrastination will take place, he will recognize that postponing to period 3 means never doing anything and will instead choose either to execute an action in period 1 or do nothing ever. In this case he must choose between u 1, 1
1, 1 1
1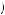 , u
, u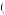 2, 1
2, 1 1
1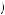 and u
and u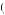 0, −
0, −  −
−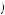 in the first period.
in the first period.
Given the complexity of varying perceptions and anticipated beliefs, an example might make this clearer. Suppose that β = 0.6, and β = 1. Thus Kerry will discount the next period according to β = 0.6, but believes that when the next period arrives, he will
|
|
|
|
Of Sophisticates and Naïfs |
|
373 |
|
discount the following period according to β = 1 (no discounting). Consider an example where v1 = 11, c1 = 0, and v2 = 20, c2 = 40. In considering the options Kerry thinks he will perceive upon entering period 2 from the perspective of period 1, the five options are
Execute x1 |
in period 2: |
u 1, 2 2 |
= |
1 |
11 |
|
|
1 − δ |
|||||
Execute x2 |
in period 2: |
u 2, 2 2 |
= |
1 |
20 − 40 |
|
|
|
|||||
1 − δ |
||||||
Execute x1 |
in period 3: |
u 1, 3 2 |
= |
|
δ |
11 |
|
|
|||||
|
1 − δ |
|||||
Execute x2 |
in period 3: |
u 2, 3 2 |
= |
|
δ |
20 − 40 |
|
|
|||||
|
1 − δ |
|||||
Do nothing |
u 0, − − = 0 |
|
||||
|
|
|
|
|
|
|
Kerry doesn’t believe he will discount quasi-hyperbolically after the first period, so he thinks all future decisions will be time consistent. Of these options, u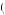 1, 3
1, 3 2
2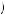 < u
< u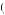 1, 2
1, 2 2
2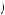 , u
, u 2, 3
2, 3 2
2 < u
< u 2, 2
2, 2 2
2 , and u
, and u 0, −
0, −  −
−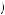 < u
< u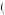 1, 2
1, 2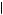 2
2 , and thus postponing action until the third period or doing nothing would be eliminated from consideration. Kerry will anticipate completing task 1 in the second period, given nothing is done in the first period, if u
, and thus postponing action until the third period or doing nothing would be eliminated from consideration. Kerry will anticipate completing task 1 in the second period, given nothing is done in the first period, if u 1, 2
1, 2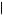 2
2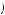 > u
> u 2, 2
2, 2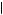 2
2 or δ < 31
or δ < 31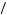 40 = 0.775. Otherwise, he will anticipate completing action 2. In the first period he discounts all future outcomes by β = 0.6 and thus chooses among
40 = 0.775. Otherwise, he will anticipate completing action 2. In the first period he discounts all future outcomes by β = 0.6 and thus chooses among
|
Execute x1 |
in period 1: |
u 1, 1 1 |
= |
0.6 |
11 |
|
|
||
|
|
1 − δ |
|
|
||||||
Execute x2 |
in period 1: |
u 2, 1 1 |
= |
0.6 |
20 − 40 |
|||||
|
|
|
||||||||
1 − δ |
||||||||||
|
|
|
|
|
|
|
|
δ |
||
Execute xi in period 2: |
u i, 2 1 |
= 0.6 |
|
vi − ci |
||||||
1 − δ |
||||||||||
|
Do nothing |
|
u 0, − − = 0 |
|
|
|
||||
|
|
|
|
|
|
|
|
|
||
Again, doing nothing is dominated |
by the option |
to do x1 in period 1. Also, |
||||||||
u 1, 1 1 > u 2, 1 1 if δ < 173 200 = 0.865, implying x2 |
in period 1 would never be |
|||||||||
chosen if δ were below this number, and x1 in period 1 would never be chosen if δ were above this number. If δ < 0.775, then Kerry will always choose to complete action x1 immediately because u 1, 1
1, 1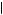 1
1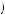 > u
> u 1, 2
1, 2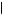 1
1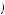 . If 0.775 < δ < 0.865, then Kerry must choose between x1 in period 1 and x2 in period 2. In this case, u
. If 0.775 < δ < 0.865, then Kerry must choose between x1 in period 1 and x2 in period 2. In this case, u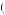 1, 1
1, 1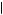 1
1 > u
> u 2, 2
2, 2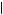 1
1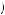 implies that
implies that
δ< 153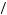 180 = 0.850. Thus, Kerry chooses to complete task x1 immediately if δ < 0.850. However, if 0.850 < δ < 0.865, Kerry plans to postpone and perform x2 in the next period, though in each period thereafter he will actually decide to continue to postpone because the same decision process is repeated. If δ > 0.865, then Kerry must decide
180 = 0.850. Thus, Kerry chooses to complete task x1 immediately if δ < 0.850. However, if 0.850 < δ < 0.865, Kerry plans to postpone and perform x2 in the next period, though in each period thereafter he will actually decide to continue to postpone because the same decision process is repeated. If δ > 0.865, then Kerry must decide
between performing x2 immediately, or performing x2 in the next period. In this case, u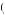 2, 1
2, 1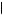 1
1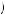 > u
> u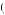 2, 2
2, 2 1
1 implies δ > 1. Thus, Kerry always chooses to procrastinate eternally if
implies δ > 1. Thus, Kerry always chooses to procrastinate eternally if
δ> 0.850.
