
- •Brief Contents
- •Contents
- •Preface
- •Who Should Use this Book
- •Philosophy
- •A Short Word on Experiments
- •Acknowledgments
- •Rational Choice Theory and Rational Modeling
- •Rationality and Demand Curves
- •Bounded Rationality and Model Types
- •References
- •Rational Choice with Fixed and Marginal Costs
- •Fixed versus Sunk Costs
- •The Sunk Cost Fallacy
- •Theory and Reactions to Sunk Cost
- •History and Notes
- •Rational Explanations for the Sunk Cost Fallacy
- •Transaction Utility and Flat-Rate Bias
- •Procedural Explanations for Flat-Rate Bias
- •Rational Explanations for Flat-Rate Bias
- •History and Notes
- •Theory and Reference-Dependent Preferences
- •Rational Choice with Income from Varying Sources
- •The Theory of Mental Accounting
- •Budgeting and Consumption Bundles
- •Accounts, Integrating, or Segregating
- •Payment Decoupling, Prepurchase, and Credit Card Purchases
- •Investments and Opening and Closing Accounts
- •Reference Points and Indifference Curves
- •Rational Choice, Temptation and Gifts versus Cash
- •Budgets, Accounts, Temptation, and Gifts
- •Rational Choice over Time
- •References
- •Rational Choice and Default Options
- •Rational Explanations of the Status Quo Bias
- •History and Notes
- •Reference Points, Indifference Curves, and the Consumer Problem
- •An Evolutionary Explanation for Loss Aversion
- •Rational Choice and Getting and Giving Up Goods
- •Loss Aversion and the Endowment Effect
- •Rational Explanations for the Endowment Effect
- •History and Notes
- •Thought Questions
- •Rational Bidding in Auctions
- •Procedural Explanations for Overbidding
- •Levels of Rationality
- •Bidding Heuristics and Transparency
- •Rational Bidding under Dutch and First-Price Auctions
- •History and Notes
- •Rational Prices in English, Dutch, and First-Price Auctions
- •Auction with Uncertainty
- •Rational Bidding under Uncertainty
- •History and Notes
- •References
- •Multiple Rational Choice with Certainty and Uncertainty
- •The Portfolio Problem
- •Narrow versus Broad Bracketing
- •Bracketing the Portfolio Problem
- •More than the Sum of Its Parts
- •The Utility Function and Risk Aversion
- •Bracketing and Variety
- •Rational Bracketing for Variety
- •Changing Preferences, Adding Up, and Choice Bracketing
- •Addiction and Melioration
- •Narrow Bracketing and Motivation
- •Behavioral Bracketing
- •History and Notes
- •Rational Explanations for Bracketing Behavior
- •Statistical Inference and Information
- •Calibration Exercises
- •Representativeness
- •Conjunction Bias
- •The Law of Small Numbers
- •Conservatism versus Representativeness
- •Availability Heuristic
- •Bias, Bigotry, and Availability
- •History and Notes
- •References
- •Rational Information Search
- •Risk Aversion and Production
- •Self-Serving Bias
- •Is Bad Information Bad?
- •History and Notes
- •Thought Questions
- •Rational Decision under Risk
- •Independence and Rational Decision under Risk
- •Allowing Violations of Independence
- •The Shape of Indifference Curves
- •Evidence on the Shape of Probability Weights
- •Probability Weights without Preferences for the Inferior
- •History and Notes
- •Thought Questions
- •Risk Aversion, Risk Loving, and Loss Aversion
- •Prospect Theory
- •Prospect Theory and Indifference Curves
- •Does Prospect Theory Solve the Whole Problem?
- •Prospect Theory and Risk Aversion in Small Gambles
- •History and Notes
- •References
- •The Standard Models of Intertemporal Choice
- •Making Decisions for Our Future Self
- •Projection Bias and Addiction
- •The Role of Emotions and Visceral Factors in Choice
- •Modeling the Hot–Cold Empathy Gap
- •Hindsight Bias and the Curse of Knowledge
- •History and Notes
- •Thought Questions
- •The Fully Additive Model
- •Discounting in Continuous Time
- •Why Would Discounting Be Stable?
- •Naïve Hyperbolic Discounting
- •Naïve Quasi-Hyperbolic Discounting
- •The Common Difference Effect
- •The Absolute Magnitude Effect
- •History and Notes
- •References
- •Rationality and the Possibility of Committing
- •Commitment under Time Inconsistency
- •Choosing When to Do It
- •Of Sophisticates and Naïfs
- •Uncommitting
- •History and Notes
- •Thought Questions
- •Rationality and Altruism
- •Public Goods Provision and Altruistic Behavior
- •History and Notes
- •Thought Questions
- •Inequity Aversion
- •Holding Firms Accountable in a Competitive Marketplace
- •Fairness
- •Kindness Functions
- •Psychological Games
- •History and Notes
- •References
- •Of Trust and Trustworthiness
- •Trust in the Marketplace
- •Trust and Distrust
- •Reciprocity
- •History and Notes
- •References
- •Glossary
- •Index
|
|
|
|
Does Prospect Theory Solve the Whole Problem? |
|
267 |
|
Does Prospect Theory Solve the Whole Problem?
Prospect theory is relatively effective in explaining the majority of decisions under risk observed in the laboratory and many behaviors observed in the field. However, most of these risks take on a very specialized form. The majority of risks presented in this chapter and in Chapter 9 are dichotomous choice problems. In other words, the decision maker can choose either to take the gamble or to reject it. Further, most of the gambles we have discussed can result in only a small set of discrete outcomes. In many cases there are only two or three possible outcomes. The majority of risky decisions that are studied by economists are not so simple. If we wished to study investment behavior, each investor has a nearly infinite choice of potential combinations of stocks, bonds, real assets, or commodities they can choose to invest their money in. Moreover, they may invest any amount of money they have access to. Thus, most interesting investment decisions are not dichotomous. Moreover, most investments have potential payoffs in a very wide range. One might lose all one’s investment, might double it, or might fall anywhere in between. The lack of realism in the laboratory has caused many to question the veracity of prospect theory and other behavioral models of decision under risk. Perhaps these models only work when facing this very specialized set of decision problems.
Graham Loomes was one of the first researchers to explore continuous-choice investment in a laboratory setting. He designed a special experiment to mirror, in a limited way, the common investment problem. In Decision 1, he endowed his participants with $20 that they could allocate between two investments, A1 and B1. In the standard investment problem, investors must invest their money in a wide array of investments that might have different payoffs depending on the outcome. Typically, investors reduce the amount of risk they face by diversifying their portfolio of investments. Participants in Loomes’ experiment had a probability of 0.6 of receiving the amount invested in A1 and a probability of 0.4 of receiving the amount invested in B1. An expected utility maximizer would solve
maxA1 ≤ 200.6U A1 + 0.4U 20 − A1 . |
10 18 |
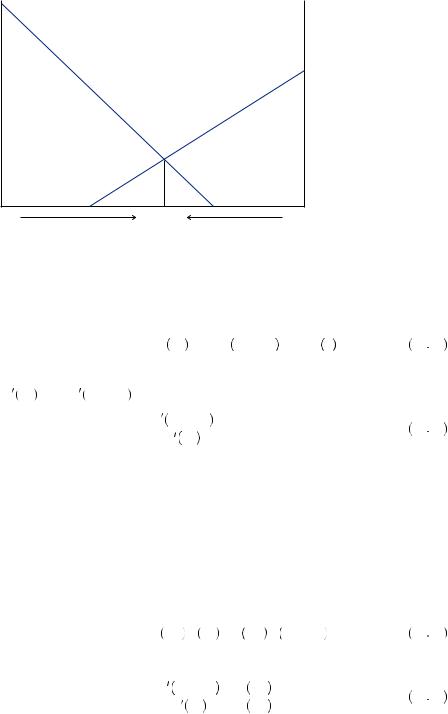
The solution to equation 10.18 occurs where the expected marginal utility between the two investments is equal. This is depicted in Figure 10.9, where the vertical axis is the marginal utility weighted by the probability of a particular outcome, and the horizontal axis measures the allocation between investments A1 and A2. As you move to the right in the figure, the allocation to A1 increases and the allocation to B1 decreases. The curve labeled 0.6U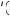 A1
A1 represents the probability of outcome A1, which is 0.6, multiplied by the marginal utility of wealth given the allocation,U
represents the probability of outcome A1, which is 0.6, multiplied by the marginal utility of wealth given the allocation,U A1
A1 . One should continue to increase the allocation to A1 until the weighted marginal utility from A1 is equal to the weighted marginal utility from B1, the curve labeled 0.4U
. One should continue to increase the allocation to A1 until the weighted marginal utility from A1 is equal to the weighted marginal utility from B1, the curve labeled 0.4U B1
B1 . This point is depicted in the figure as
. This point is depicted in the figure as  A*1, B*1
A*1, B*1 . This occurs where 0.6U
. This occurs where 0.6U A1
A1 = 0.4U
= 0.4U 20 − A1
20 − A1 , assuming that it is not optimal to put all of the money in one of the investments.
, assuming that it is not optimal to put all of the money in one of the investments.
These first-order conditions can be written as
U 20 − A1 |
= |
0.6 |
= 1.5. |
10 19 |
U A1 |
|
|||
0.4 |
|
|
||
|
|
|
|
|
268 |
|
PROSPECT THEORY AND DECISION UNDER RISK OR UNCERTAINTY |
FIGURE 10.9
The Optimal Allocation in Loomes’ Portfolio Problem
utility |
0.6Uʹ (A1) |
|
|
|
|
Weighted marginal |
|
0.4Uʹ (B1) |
|
|
|
A1 |
(A*1, B*1) |
B1 |
For Decision 2, participants were then given another $20 and asked to allocate it between A2 and B2. However, this time they were told that there was a probability of 0.3 of receiving A2 and 0.2 of receiving B2. They would receive nothing with the remaining probability, 0.5. In this case, an expected utility maximizer would solve
maxA2 ≤ 20 0.3U A2 + 0.2U 20 − A2 |
+ 0.5U 0 , |
10 20 |
||
where equating the expected marginal |
utility of |
the two investments |
yields |
|
0.3U A2 = 0.4U 20 − A2 , which can be rewritten as |
|
|
||
|
U 20 − A2 |
= 0.3 = 1.5. |
10 21 |
|
|
U A2 |
|||
|
0.2 |
|
|
|
Because the ratio of the marginal utilities in equations 10.19 and 10.20 are both equal to 1.5, any expected-utility maximizer must choose A1 = A2 and B1 = B2. This is because Decision 2 is proportional to Decision 1. It is equivalent to a two-stage problem in which the first stage results in playing Decision 1 with 0.5 probability, and a payoff of $0 with 0.5 probability. Of 85 participants, 24 chose A1 = A2 and B1 = B2. Of the remaining, 1 chose A2 > A1, and 60 (the majority of participants) chose A1 > A2.
Notably, expected utility does not describe the behavior of the majority of participants. What about alternative theories? Consider any of the models that use probability weights (including prospect theory). In this case, the decision maker in Decision 1 would solve the problem
maxA1 ≤ 20π 0.6 U A1 + π 0.4 U 20 − A1 , |
10 22 |
resulting in the solution described by
U 20 − A1 |
= |
π 0.6 |
. |
10 23 |
U A1 |
|
|||
|
π 0.4 |
|
||

|
|
|
|
|
|
|
|
|
|
|
Prospect Theory and Risk Aversion in Small Gambles |
|
269 |
|
|||||
Decision 2 would have the decision maker solve |
|
|
|
|
|
|
|||
maxA2 ≤ 20π 0.3 U A2 + π 0.2 U 20 − A2 + π 0.5 U 0 , |
10 24 |
|
|
|
|||||
with solution given by |
|
|
|
|
|
|
|
|
|
U 20 − A2 |
= |
π |
0.3 |
. |
10 25 |
|
|
|
|
|
U A2 |
|
0.2 |
|
|
||||
|
π |
|
|
|
|
|
|||
Equations 10.23 and 10.25 imply different allocations in the decision problems owing to the distortion of probabilities through the probability-weighting function. However, probability-weighting functions are believed to cross the 45-degree line at somewhere between 0.3 and 0.4. Above this, the probability weight should be lower than the
probability, and below this it should be higher than the probability. Thus, |
π 0.6 |
< |
π 0.3 |
, |
||||
|
π 0.2 |
|||||||
π 0.4 |
||||||||
implying that |
U 20 − A1 |
< |
U 20 − A2 |
. Given that all outcomes are coded as gains, people |
||||
U A1 |
|
|||||||
|
|
U A2 |
|
|
|
|
||
should display risk aversion, meaning that marginal utility is declining for larger rewards. Thus, U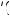 20 − A
20 − A gets larger for larger values of A, and U
gets larger for larger values of A, and U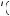 A
A gets smaller for
gets smaller for
larger values of A, implying that U 20 − A |
U A increases as A increases. Recall that |
|||
probability weights lead us to believe that |
U 20 − A1 |
< |
U 20 − A2 |
, so that A1 < A2, the |
U A1 |
|
|||
|
|
U A2 |
||
outcome observed in exactly 1 of 85 participants. The majority of participants behave in a way that is inconsistent with the probability-weighting model. Although no alternative theory has come to prominence to explain this anomaly, it may be a signal that con- tinuous-choice problems result from very different behaviors than the simple dichoto- mous-choice problems that are so common in the laboratory.
Prospect Theory and Risk Aversion
in Small Gambles
Further evidence that we might not fully understand how risky choices are made can be found by examining the small-risk problem identified by Matthew Rabin and discussed in Chapter 6. If we attempt to explain any risk-averse behavior using expected utility theory, the only tool with which we can explain it is diminishing marginal utility of wealth, or concavity of the utility function. The most fundamental principle of calculus is the observation that continuous functions are approximately linear over short intervals. Thus, when small amounts of money are at stake, a utility of wealth function should be approximately linear, implying local risk neutrality. If instead, we observe risk-averse behavior over very small gambles, this then implies that the utility function must be extremely concave, and unreasonably so. This led Rabin to derive the following theorem (see Chapter 6 for a full discussion and greater intuition).

|
|
|
|
|
270 |
|
PROSPECT THEORY AND DECISION UNDER RISK OR UNCERTAINTY |
Suppose that for all w, U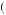 w
w is strictly increasing and weakly concave. Suppose there exists g > l > 0, such that for all w, the person would reject a 0.50 probability of receiving g and a 0.50 probability of losing l. Then the person would also turn down a bet with 0.50 probability of gaining mg and a 0.50 probability of losing 2kl, where k is any positive integer and m < m
is strictly increasing and weakly concave. Suppose there exists g > l > 0, such that for all w, the person would reject a 0.50 probability of receiving g and a 0.50 probability of losing l. Then the person would also turn down a bet with 0.50 probability of gaining mg and a 0.50 probability of losing 2kl, where k is any positive integer and m < m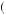 k
k , where
, where
|
ln 1 − |
1 − |
|
l |
k − 1 |
g i |
|
|
|
|
|
|
||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
||
|
g |
l |
|
|
|
|
|
|
||||||
|
|
|
i = 0 |
1 − |
1 − |
l |
|
|||||||
|
|
|
|
|
|
|
|
if |
2 |
|||||
|
|
|
|
|
|
|
|
|
|
|||||
m k = |
|
ln |
l g |
|
|
|
|
|
g |
|
||||
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
if |
1 − |
1 − |
l |
|
2 |
|
|
|
|
|
|
|
|
|
g |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
k − 1 |
|
g |
i |
||
i = 0 |
|
|
|
> 0 |
|
|
l |
||||
|
|
||||
k − 1 |
g |
i |
|||
|
|
|
|
≤ 0. |
|
i = 0 |
l |
||||
|
|||||
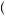 10
10 26
26
On its face, this is difficult to interpret without an example. Consider someone who would turn down an 0.50 probability of gaining $120 and 0.50 probability of losing $100. If this person were strictly risk averse and behaved according to expected utility theory, then the person would also turn down any bet that had a 0.50 probability of losing $600, no matter how large the possible gain. Although it seems reasonable that people might want to turn down the smaller gamble, it seems unreasonable that virtually anyone would turn down such a cheap bet for a 50 percent probability of winning an infinite amount of money. Several other examples are given in Table 10.2. Rabin takes this as further evidence that people are susceptible to loss aversion. Note that we relied on the smoothness and concavity of the utility function to obtain this result. Loss aversion does away with smoothness, allowing a kink in the function at the reference point. Thus, no matter how small the gamble, no line approximates the value function, and severely risk averse behavior is still possible in small gambles without implying ridiculous behavior in larger gambles. As demonstrated in Table 10.2, often what economists call a small amount is not very small at all. In general, when we talk about small risks, we mean that the risk is small in relation to some other gamble.
William Neilson notes that the problem is not exclusive to expected utility. If, for example, we use expected utility with rank-dependent weights, we can derive the following analogous theorem:
Suppose that for all w, U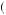 w
w is strictly increasing and weakly concave. Let π be a probability-weighting function, with p = π − 1
is strictly increasing and weakly concave. Let π be a probability-weighting function, with p = π − 1  12
12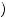 . Suppose there exists g > l > 0, such that for all w, a rank-dependent expected-utility maximizer would reject a p probability of receiving g and a
. Suppose there exists g > l > 0, such that for all w, a rank-dependent expected-utility maximizer would reject a p probability of receiving g and a 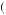 1 − p
1 − p probability of losing l. Then the person would also turn down a bet with p probability of gaining mg and a
probability of losing l. Then the person would also turn down a bet with p probability of gaining mg and a  1 − p
1 − p probability of losing 2kl, where k is any positive integer, and m < m
probability of losing 2kl, where k is any positive integer, and m < m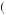 k
k , where m
, where m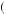 k
k is defined in equation 10.26.
is defined in equation 10.26.
Thus, the previous example would hold if we simply adjust the probabilities to those that result in probability weights of 0.5. For example, using the estimates from Tversky

|
|
|
|
|
|
|
|
|
Prospect Theory and Risk Aversion in Small Gambles |
|
271 |
|
|||
Table 10.2 Examples Applying Rabin’s Theorem |
|
|
|
|
|||
|
|
|
|
|
|
||
If You Would Turn Down |
|
Then You Should Also Turn Down |
|
|
|
||
|
|
|
|
|
|
|
|
Winning with |
Losing with 0.5 |
|
Winning with |
Losing with 0.5 |
|
|
|
0.5 Probability |
Probability |
|
0.5 Probability |
Probability |
|
|
|
|
|
|
|
|
|
|
|
$110 |
− $100 |
$555 |
− $400 |
|
|
|
|
|
|
$1,062 |
− $600 |
|
|
|
|
|
|
$ |
− $1,000 |
|
|
|
|
$550 |
− $500 |
$2,775 |
− $2000 |
|
|
|
|
|
|
$5313 |
− $3000 |
|
|
|
|
|
|
$ |
− $5000 |
|
|
|
|
$1,100 |
− $1,000 |
$5,551 |
− $4000 |
|
|
|
|
|
|
$10,628 |
− $6000 |
|
|
|
|
|
|
$ |
− $10,000 |
|
|
|
|
|
|
|
|
|
|
|
|
and Kahneman for the rank-dependent weighting function, a probability weight of 0.5 would correspond to a probability of 0.36 for the gain and 0.64 for the loss. Thus, anyone who would turn down a 0.36 probability chance of winning $120 and a 0.64 probability of losing $100 would also turn down any bet that had a 0.64 probability of losing $600 no matter how much they could win with the other 0.36 probability. Similar results would hold for all of the examples in Table 10.2.
By itself this might not seem damaging to prospect theory because we could still argue that this result is abolished by the kink at reference point. However, this only shifts the problem. Consider, for example, the case where the person has the choice between a gain of $600 or a gamble that would yield either $720 with probability 0.36 or $500 with probability 0.64. If they would choose the $600, and classify it as a $600 gain, then they would also rather have $600 than any gamble that would yield $0 with probability 0.64, no matter how much could be had with the other 0.36 probability. Note that this argument only holds if the $600 is considered a gain. If instead it is incorporated in the reference point, the problem goes away as it did before. One might therefore argue that the $600 would be treated as the new reference point. Nonetheless, it is possible to engineer clever gambles for which it would seem inappropriate for the $600 to be treated as the reference point and that produce similar results. One must remember that models are approximations and simplifications of how decisions are made. Thus, it is always possible to push the limits of the model beyond its reasonable application. This may be especially true of behavioral models that are not intended to provide a single unifying theory of behavior but rather a contextually appropriate description of regularly observed phenomena.
 EXAMPLE 10.6 Sweating the Small Stuff
EXAMPLE 10.6 Sweating the Small Stuff
When purchasing a home, a buyer is most often required by the lending agency to purchase some form of homeowners insurance. However, the bank generally gives homeowners wide flexibility in the structure of the insurance they purchase, allowing applicants to choose what types of added coverage they would like as well as the

|
|
|
|
|
272 |
|
PROSPECT THEORY AND DECISION UNDER RISK OR UNCERTAINTY |
deductible if a claim is filed. When purchasing insurance, a homeowner agrees to pay the insurance company an annual premium. In return, the insurance company agrees to write a check to the homeowner in the event of damage due to a specified list of events. This check will be enough to pay for repairs to the home or items in the home that are covered, minus the insurance deductible. For example, a homeowner who suffered $35,000 of damage from a tornado and who carried insurance with a $1,000 deductible would receive a check for $34,000. The deductible can also have an impact on whether a claim is filed. For example, a homeowner who suffered only $700 worth of damage would not likely file a claim if the deductible was $1,000 because the claim would not result in any payment by the insurance company.
The deductible allows the homeowner to share some of the risk with the insurance company in return for a lower annual premium. Also, because homeowners are offered a schedule of possible premiums and deductibles, the choice of deductible can offer a window into the homeowner’s risk preferences. A homeowner who is risk loving might not want the insurance in the first place, only buying it because the lender requires it. In this case, she will likely opt for a very high deductible, sharing a greater portion of the risk in return for a much lower average cost. For example, a home valued at $181,700 would be covered for premiums of $504 with a $1,000 deductible. The same home could be insured for an annual premium of $773 with a $100 deductible. Standard policies specify a $1,000, $500, $250, or $100 deductible. Justin Snydor used data from 50,000 borrowers to examine how buyers choose the level of deductible and also to examine the risk tradeoffs involved. The plurality of buyers (48 percent) chose a policy with a $500 deductible. Another 35 percent chose a $250 deductible. A much smaller percentage (17 percent) chose the $1,000 deductible, and a vanishingly small 0.3 percent chose the $100 deductible.
Table 10.3 displays the average annual premium offered to homeowners by level of deductible. Consider a risk-neutral homeowner who is choosing between a $1,000 deductible and a $500 deductible. Choosing the $500 deductible means that the homeowner will pay about $100 more  $715 − $615
$715 − $615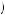 with certainty to lower the cost of repairs by $500 (the difference in the deductibles) in the event of damage greater than $500. We do not know the probability of filing a claim greater than $500. However, if we call the probability of filing a $500 claim p500, then a risk-neutral buyer should prefer the $500 deductible to the $1,000 deductible if
with certainty to lower the cost of repairs by $500 (the difference in the deductibles) in the event of damage greater than $500. We do not know the probability of filing a claim greater than $500. However, if we call the probability of filing a $500 claim p500, then a risk-neutral buyer should prefer the $500 deductible to the $1,000 deductible if
p500 |
$500 > $100 |
10 27 |
This implies that p500 > 0.20. Although we don’t know the actual probability of filing a claim, we know that only 0.043 claims were filed per household, meaning that a
Table 10.3 Homeowners Insurance Policies
|
Average |
Annual Number of Paid |
Percentage |
|
Deductible |
Annual Premium |
Claims per Household |
Selecting |
|
|
|
|
|
|
$1,000 |
$615.82 |
0.025 |
17 |
|
$500 |
$715.73 |
0.043 |
48 |
|
$250 |
$802.32 |
0.049 |
35 |
|
$100 |
$935.54 |
0.047 |
0.3 |
|
|
|
|
|
|

|
|
|
|
Prospect Theory and Risk Aversion in Small Gambles |
|
273 |
|
maximum of 4.3 percent of households filed a claim (some households might have filed multiple claims). Thus, it is likely that the probability of a claim is closer to 0.04—very small relative to 0.20. For the choice between the $500 deductible and the $250 deductible, the homeowner is paying an additional $85  $801 − $716
$801 − $716 a year for a p$250 probability of receiving $250 (the difference between the $500 deductible and the $250 deductible). In this case, a risk-neutral homeowner would prefer the $250 deductible if
a year for a p$250 probability of receiving $250 (the difference between the $500 deductible and the $250 deductible). In this case, a risk-neutral homeowner would prefer the $250 deductible if
p250 |
$250 > $85. |
10 28 |
This implies that p250 > 0.34, yet only 0.049 claims are filed on average each year. Anyone choosing the $500 or the $250 deductible is clearly paying more than the
expected value of the added insurance, suggesting that the homeowners are severely risk averse. But just how risk averse are they? This is difficult to know with the limited information we have. An expected-utility maximizer should choose the deductible that solves
maxiqU w − Di − ri + 1 − q U w − ri , |
10 29 |
where i can be $1,000, $500, $250, or $100, q is the probability of damage requiring a claim, Di is the deductible i, ri is the annual premium for the policy with deductible i, and U denotes the utility of wealth function. By specifying the utility function as1
U w = |
x |
1 − p |
10 30 |
|
|
|
, |
||
1 |
|
|||
|
− p |
|
||
and using the claim rate (column 3 of Table 10.3) as a probability of damage, Snydor is able to place some bounds on the parameter ρ for each person in the dataset. This parameter is a measure of risk aversion. The higher ρ, the more risk averse the homeowner. Using this lower bound, Snydor is able then to determine whether a buyer with the same level of ρ would be willing to take a gamble consisting of a 0.50 probability of gaining some amount of money G and an 0.50 probability of losing $1,000, much like Rabin’s calibration theorem. In fact, he finds that in all cases, more than 92 percent of all homeowners should be unwilling to take a gamble that has a 0.50 probability of losing $1,000 no matter how much money could be had with the other 0.50 probability. This clearly suggests that the level of risk aversion homeowners display is beyond the level we might consider reasonable.
The alternative explanation, prospect theory, would not provide a solution to this problem under normal definitions because all of the outcomes deal in losses. Examining equation 10.29, note that all possible outcomes are smaller than current wealth. In the loss domain, homeowners should be risk loving, implying they should only buy the $1,000 deductible policy, and then only because the bank forces them to. Moreover, misperception of probabilities seems unlikely as an explanation because the homeowner would need to overestimate the probability of a loss by nearly 500 percent. Suppose, for example, that we consider the simplest form of the loss-averse value function consisting of just two line segments:
1 Commonly called the constant relative risk aversion form.

|
|
|
|
|
|
|
|
|
|
|
274 |
|
PROSPECT THEORY AND DECISION UNDER RISK OR UNCERTAINTY |
||||||
|
|
|
|
V x = |
x |
if x ≥ 0 |
10 31 |
||
|
|
|
|
βx if x < 0 , |
|||||
|
|
where β > 1. If homeowners value money outcomes according to equation 10.31, and if |
|||||||
|
|
they regard premiums as a loss, then the homeowner will prefer the $500 deductible to |
|||||||
|
|
the $1,000 deductible if |
|
|
|
|
|
|
|
|
|
|
π q V − 500 − 715 + 1 − π q |
V |
− 715 |
||||
|
|
|
> π q V |
− 1000 − 615 + 1 − π q |
10 32 |
||||
|
|
|
V − 615 |
||||||
|
|
or, substituting equation 10.31 into equation 10.32 |
|
|
|||||
|
|
|
β π q |
− 1215 + 1 − π q |
− 715 |
||||
|
|
|
> β π q − 1615 + 1 − π q |
|
10 33 |
||||
|
|
|
|
− 615 . |
|||||
|
|
Simplifying, the homeowner will prefer the smaller deductible if |
|||||||
|
|
|
|
|
π q |
> 0.25. |
|
10 34 |
|
|
|
|
|
|
|
||||
|
|
|
|
|
1 − π q |
|
|||
But given that the probability of a loss is closer to 0.04, and given the parameters of the weighting function presented earlier in the chapter, π q
q
 1 − π
1 − π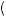 q
q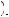
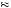 0.11. Thus probability weighting alone cannot account for the severely risk-averse behavior.
0.11. Thus probability weighting alone cannot account for the severely risk-averse behavior.
Segregation may be the key to this puzzle. If the homeowner did not perceive the premium as a loss (segregating the payment), prospect theory would suggest that she would then prefer the $500 deductible if the difference in the expected value of V between the two outcomes exceeds the change in price. Or,
π q V |
− 500 + 1 − π q V 0 − 715 |
|
> π q |
V − 1000 + |
10 35 |
1 − π q V 0 − 615. |
||
Note here that the value paid for the premium is not considered in the value function because it is segregated. Homeowners do not consider it a loss because it is a planned expense. Substituting equation 10.31 into equation 10.35 we obtain
− π q β500 − 715 > − π q β1000 − 615 |
10 36 |
or |
|
βπ q > 0.2. |
10 37 |
If we assume q  0.4, then π
0.4, then π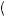 q
q
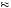 0.1. Additionally, the value of β is commonly thought to be just above 2, suggesting that prospect theory with segregation of the annual premium might explain some insurance behavior.
0.1. Additionally, the value of β is commonly thought to be just above 2, suggesting that prospect theory with segregation of the annual premium might explain some insurance behavior.
