
- •Brief Contents
- •Contents
- •Preface
- •Who Should Use this Book
- •Philosophy
- •A Short Word on Experiments
- •Acknowledgments
- •Rational Choice Theory and Rational Modeling
- •Rationality and Demand Curves
- •Bounded Rationality and Model Types
- •References
- •Rational Choice with Fixed and Marginal Costs
- •Fixed versus Sunk Costs
- •The Sunk Cost Fallacy
- •Theory and Reactions to Sunk Cost
- •History and Notes
- •Rational Explanations for the Sunk Cost Fallacy
- •Transaction Utility and Flat-Rate Bias
- •Procedural Explanations for Flat-Rate Bias
- •Rational Explanations for Flat-Rate Bias
- •History and Notes
- •Theory and Reference-Dependent Preferences
- •Rational Choice with Income from Varying Sources
- •The Theory of Mental Accounting
- •Budgeting and Consumption Bundles
- •Accounts, Integrating, or Segregating
- •Payment Decoupling, Prepurchase, and Credit Card Purchases
- •Investments and Opening and Closing Accounts
- •Reference Points and Indifference Curves
- •Rational Choice, Temptation and Gifts versus Cash
- •Budgets, Accounts, Temptation, and Gifts
- •Rational Choice over Time
- •References
- •Rational Choice and Default Options
- •Rational Explanations of the Status Quo Bias
- •History and Notes
- •Reference Points, Indifference Curves, and the Consumer Problem
- •An Evolutionary Explanation for Loss Aversion
- •Rational Choice and Getting and Giving Up Goods
- •Loss Aversion and the Endowment Effect
- •Rational Explanations for the Endowment Effect
- •History and Notes
- •Thought Questions
- •Rational Bidding in Auctions
- •Procedural Explanations for Overbidding
- •Levels of Rationality
- •Bidding Heuristics and Transparency
- •Rational Bidding under Dutch and First-Price Auctions
- •History and Notes
- •Rational Prices in English, Dutch, and First-Price Auctions
- •Auction with Uncertainty
- •Rational Bidding under Uncertainty
- •History and Notes
- •References
- •Multiple Rational Choice with Certainty and Uncertainty
- •The Portfolio Problem
- •Narrow versus Broad Bracketing
- •Bracketing the Portfolio Problem
- •More than the Sum of Its Parts
- •The Utility Function and Risk Aversion
- •Bracketing and Variety
- •Rational Bracketing for Variety
- •Changing Preferences, Adding Up, and Choice Bracketing
- •Addiction and Melioration
- •Narrow Bracketing and Motivation
- •Behavioral Bracketing
- •History and Notes
- •Rational Explanations for Bracketing Behavior
- •Statistical Inference and Information
- •Calibration Exercises
- •Representativeness
- •Conjunction Bias
- •The Law of Small Numbers
- •Conservatism versus Representativeness
- •Availability Heuristic
- •Bias, Bigotry, and Availability
- •History and Notes
- •References
- •Rational Information Search
- •Risk Aversion and Production
- •Self-Serving Bias
- •Is Bad Information Bad?
- •History and Notes
- •Thought Questions
- •Rational Decision under Risk
- •Independence and Rational Decision under Risk
- •Allowing Violations of Independence
- •The Shape of Indifference Curves
- •Evidence on the Shape of Probability Weights
- •Probability Weights without Preferences for the Inferior
- •History and Notes
- •Thought Questions
- •Risk Aversion, Risk Loving, and Loss Aversion
- •Prospect Theory
- •Prospect Theory and Indifference Curves
- •Does Prospect Theory Solve the Whole Problem?
- •Prospect Theory and Risk Aversion in Small Gambles
- •History and Notes
- •References
- •The Standard Models of Intertemporal Choice
- •Making Decisions for Our Future Self
- •Projection Bias and Addiction
- •The Role of Emotions and Visceral Factors in Choice
- •Modeling the Hot–Cold Empathy Gap
- •Hindsight Bias and the Curse of Knowledge
- •History and Notes
- •Thought Questions
- •The Fully Additive Model
- •Discounting in Continuous Time
- •Why Would Discounting Be Stable?
- •Naïve Hyperbolic Discounting
- •Naïve Quasi-Hyperbolic Discounting
- •The Common Difference Effect
- •The Absolute Magnitude Effect
- •History and Notes
- •References
- •Rationality and the Possibility of Committing
- •Commitment under Time Inconsistency
- •Choosing When to Do It
- •Of Sophisticates and Naïfs
- •Uncommitting
- •History and Notes
- •Thought Questions
- •Rationality and Altruism
- •Public Goods Provision and Altruistic Behavior
- •History and Notes
- •Thought Questions
- •Inequity Aversion
- •Holding Firms Accountable in a Competitive Marketplace
- •Fairness
- •Kindness Functions
- •Psychological Games
- •History and Notes
- •References
- •Of Trust and Trustworthiness
- •Trust in the Marketplace
- •Trust and Distrust
- •Reciprocity
- •History and Notes
- •References
- •Glossary
- •Index
|
|
|
|
|
162 |
|
REPRESENTATIVENESS AND AVAILABILITY |
The unconditional probability that I have drawn from urn 1 is just the probability of rolling a 1 or a 2 on a six-sided die, P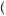 Urn 1
Urn 1 = 1
= 1 3. The probability of drawing a red ball given urn 1 is selected is just the fraction of red balls in urn 1, P
3. The probability of drawing a red ball given urn 1 is selected is just the fraction of red balls in urn 1, P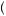 Red
Red Urn
Urn  = 4
= 4 5. Finally, the unconditional probability of drawing a red ball can be calculated as the sum of the probability of drawing red from each urn, multiplied by the probability of drawing that urn, P
5. Finally, the unconditional probability of drawing a red ball can be calculated as the sum of the probability of drawing red from each urn, multiplied by the probability of drawing that urn, P Red
Red = P
= P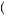 Red
Red Urn 1
Urn 1 P
P Urn 1
Urn 1 + P
+ P Red
Red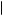 Urn 2
Urn 2 P
P Urn 2
Urn 2 , or P
, or P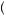 Red
Red = 4
= 4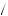 5 × 1
5 × 1 3 + 1
3 + 1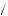 2 × 2
2 × 2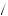 3 = 3
3 = 3 5. Thus, by equation 7.9, we can find the probability that I am drawing from urn 1, P
5. Thus, by equation 7.9, we can find the probability that I am drawing from urn 1, P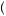 Urn 1
Urn 1 Red
Red =
= 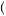 4
4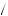 5 × 1
5 × 1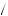 3
3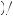
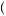 3
3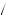 5
5 = 4
= 4 9. Thus it is more likely that I have drawn from urn 2. Economists often use Bayes’ rule as a model of learning in a market setting. It can be used as a model of price expectations or as a model of learning about competitor preferences in a game.
9. Thus it is more likely that I have drawn from urn 2. Economists often use Bayes’ rule as a model of learning in a market setting. It can be used as a model of price expectations or as a model of learning about competitor preferences in a game.
Calibration Exercises
As anyone who has ever taught statistics can tell you, people have a hard time reasoning through questions of probability. At a very basic level, people appear to have difficulty in making accurate probabilistic predictions. An example of a probabilistic prediction is found in most weather forecasts. The meteorologist predicts, for example, a 60 percent chance of rain. There are two important components of accuracy. First, it would be nice if the probabilities associated with the prediction were either near 1 or 0. In other words, a forecast of 99 percent chance of rain is probably more useful in planning activities than a 50 percent chance of rain. We refer to this component of accuracy as precision. Second, to be accurate, the probabilistic prediction must occur with the frequency suggested by the associated probability. In other words, it should rain about half the time when the meteorologist forecasts a 50 percent chance of rain. We will refer to this component of accuracy as calibration.
There is a fundamental tradeoff in accuracy and precision. Suppose you lived in an area where it rained about one of every five days. Then, without any special knowledge of the particular weather patterns at the time, the meteorologist could simply say there was a 20 percent chance of rain each day when called on for the forecast. The forecast would be well calibrated because it would truly rain about 20 percent of the time. However, most people would be frustrated by the lack of informational content in the forecast. With greater understanding of the underlying patterns, the meteorologist can begin to forecast higher probabilities on some days and lower probabilities on other days. In fact, forecasts are very well calibrated in the short run. Thus, you can rely on the forecasts, though there are limits to their precision based on the state of meteorological science.
Economists are generally well calibrated (though again not very precise) when predicting changes in the economy in the short run. However, their calibration is signifi- cantly poorer when predicting several months ahead. They tend to overstate the probability that the economy will continue on its current course. It is generally not the case that people are well calibrated. Much of this chapter and the next deals with how individual probabilistic forecasts are biased by subtle cues in the decision process or by the process used to determine the probability of a specific event.

|
|
|
|
Calibration Exercises |
|
163 |
|
EXAMPLE 7.1 Of Taxicabs and Colors
Consider the following problem proposed by Daniel Kahneman and Amos Tversky:
A cab was involved in a hit and run accident at night. Two cab companies operate in the city: a Blue Cab company, and a Green Cab company. You are given the following data: 85 percent of the cabs in the city are Green and 15 percent are Blue, and a witness at the scene identified the cab involved in the accident as a Blue Cab. This witness was tested under similar visibility conditions and made correct color identifications in 80 percent of the trial instances. What is the probability that the cab involved in the accident was a Blue Cab rather than a Green one?
This question was given to participants in several experiments. Overwhelmingly, the majority believed the probability that the cab involved in the accident was a Blue Cab was 80 percent, that being the probability that the witness identifies the correct color of the cab under similar conditions. However, this ignores the underlying probability that the cab was either Blue or Green. Bayes’ rule in this case states that the probability that the cab was Blue given that the witness identified it as Blue is given by
P Blue Witness says Blue = |
P Witness says Blue Blue P Blue |
. |
7 10 |
|||
|
||||||
|
|
P Witness says Blue |
|
|||
Here, the prior probability that |
the cab was Blue is |
P Blue |
= 0.15. The probability |
|||
that the witness identifies Blue |
given that the cab |
is Blue |
is P Witness says Blue |
|||
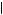 Blue
Blue = 0.80. Finally, the probability that the witness identifies Blue can be found by adding the probability that the cab is Blue times the probability that the witness identifies it as Blue given it truly is Blue to the probability that the cab is Green times the
= 0.80. Finally, the probability that the witness identifies Blue can be found by adding the probability that the cab is Blue times the probability that the witness identifies it as Blue given it truly is Blue to the probability that the cab is Green times the
probability that |
the |
witness identifies it as |
Blue given |
that it is truly |
Green. Or, |
|
P Witness says Blue |
= P Witness says Blue Blue P Blue + P Witness says Blue Green |
|||||
P Green = 0 80 |
× 0 15 + 0 20 × 0 85 = 0 29. Substituting these values obtains |
|
||||
|
P Blue Witness says Blue |
= |
0.80 × 0.15 |
0.41. |
7 11 |
|
|
|
|||||
|
|
|
0.29 |
|
|
|
Thus, when you include the baseline probability of observing a Blue Cab, it is actually more likely that the cab was Green even if the witness identified the cab as Blue.
EXAMPLE 7.2 Bingo
David Grether conducted a set of experiments in which 341 participants were asked to guess which cage a series of bingo balls was drawn from. Three bingo cages were involved. The first cage contained six balls numbered 1 to 6. A second cage contained six balls, with four marked N and two marked G. The third cage contained six balls, with three marked N and three marked G. The experiment proceeded much like the example of Bayes’ rule given earlier. Participants were put through several trials. In each trial, participants were placed so they could not see the bingo cages. They were told that a

|
|
|
|
|
164 |
|
REPRESENTATIVENESS AND AVAILABILITY |
ball would be chosen from cage 1. If a certain set of numbers came up, then a series of six balls would be drawn from cage 2. If the number drawn from cage 1 did not belong to that set, then cage 3 would be used. With each draw, the letter on the ball was announced, and then the ball was replaced into the cage so that a single ball could potentially be drawn several times. The participants were then asked to record the cage they believed the series of six drawn balls came from. In many cases, the participants received a reward for correct choices.
Participants responded to the prior probability of each cage being chosen. However, their response was very muted relative to what Bayes’ rule would predict. Consider for example the case where the sample included four balls marked N and two marked G. In this case, the sample exactly resembles the distribution of balls in cage 2. Nonetheless, the probability that we are drawing from cage 2 depends heavily on the initial conditions for the draw from cage 1. If, for example, we draw from cage 3 if the initial draw is equal to or smaller than 2, and we draw from cage 2 otherwise, Bayes’ rule yields
P Cage 2 4N2G = |
P 4N2G Cage 2 P Cage 2 |
||||||
P 4N2G Cage 2 P Cage 2 + P 4N2G Cage 3 P Cage 3 |
|
||||||
|
2 3 4 |
1 3 |
2 |
1 3 |
7 12 |
||
= |
|
0.41. |
|
||||
2 3 4 1 3 2 1 3 |
+ |
1 2 4 1 2 2 |
2 3 |
|
|||
|
|
|
|||||
However, in situations like this, the majority of people would choose cage 2 rather than cage 3. Thus, the participants appear to have looked more closely at the distribution of balls drawn than to the underlying probability of drawing from cage 2. In nearly all cases, people seemed to be swayed by how closely the draw resembled the two possible cages when making their choice than they were by the probability of drawing from either cage determined by the initial draw from cage 1.
If we were to take equation 7.12 and remove the unconditional probabilities, we would find
P 4N2G Cage 2 |
= |
2 3 4 1 3 2 |
|
2 3 4 1 3 2 + 1 2 4 1 2 2 0.58, 7 13 |
|
P 4N2G Cage 2 + P 4N2G Cage 3 |
which more closely approximates how people predicted which cage was being used. Like the cab example, the base rates seem to be ignored. However, Grether found other evidence suggesting that base rates are not altogether ignored. If the initial probability of drawing from cage 2 is 1 2, then P
2, then P Cage 2
Cage 2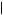 4N2G
4N2G
 0.58. Finally, if the initial probability of drawing from cage 2 is 2
0.58. Finally, if the initial probability of drawing from cage 2 is 2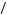 3 then P
3 then P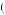 Cage 2
Cage 2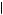 4N2G
4N2G
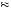 0.73. Thus, as the base rate shifts around, the resulting probability of drawing from cage 2 shifts around. Although people tended to favor the draw to the base rate when determining which cage to choose, the answers of some subjects did respond to the base rate. Uniformly, when the base probability of drawing from cage 2 was smaller, a smaller proportion of participants chose cage 2. This effect, however, was not large enough to bring the majority of participants into line with Bayes’ rule.
0.73. Thus, as the base rate shifts around, the resulting probability of drawing from cage 2 shifts around. Although people tended to favor the draw to the base rate when determining which cage to choose, the answers of some subjects did respond to the base rate. Uniformly, when the base probability of drawing from cage 2 was smaller, a smaller proportion of participants chose cage 2. This effect, however, was not large enough to bring the majority of participants into line with Bayes’ rule.
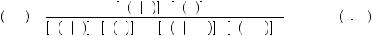
|
|
|
|
Representativeness |
|
165 |
|
Representativeness
The behavior in both of these examples shows what has become known as the representativeness heuristic. According to Daniel Kahneman and Amos Tversky, people who display the representativeness heuristic determine the probability of an event by the degree to which the event is similar in essential characteristics to its parent population and reflects the salient features of the process by which it is generated. In a framework of Bayesian updating, this leads to a situation in which base rates are either discounted or ignored altogether.
In Grether’s experiment this is relatively easy to see. The draw of bingo balls from either cage could end up having distributions that are either identical to or close to the distributions of balls in one or the other cages. With an even distribution of N and G balls as in cage 3, it is not that unlikely to draw a sample of four N balls and two G balls. But if we did not know the probability associated with the draw from cage 1, a sample of balls with four N balls and two G balls would more probably have originated with cage 2. Given a relatively low probability of selecting cage 2 from the initial draw, it very quickly becomes less probable that the given sample was from cage 2. Nonetheless, the sample looks like cage 2. In this sense, the sample is more representative of cage 2 than of cage 3. Thus, it becomes easier to convince oneself that the draw was more probably from cage 2.
In the taxicab example, the witness identifies the taxicab as being Blue. At that point, either the taxicab is Blue and the witness is correct or the taxicab is Green and the witness is wrong. We are told the witness is 80 percent accurate. Thus, the case of the witness identifying the taxicab as being Blue is much more representative of the case in which the taxicab is actually Blue. In both cases, the information in the prior is ignored. This form of representativeness is often called base rate neglect.
Grether formalizes a model of base rate neglect based on the generalized Bayes rule. Because he found that people did not ignore base rates altogether, but appeared simply to discount them, he was interested in determining how large a role the base rate, or prior, played in forming beliefs. The generalized Bayes rule can be written as
P A B = |
P B A βL P A βP |
|
P B A βL P A βP + P B − A βL P − A βP , |
7 14 |
where − A is the set of all possible events that exclude A, βL is a parameter representing the weight placed on the likelihood information, and βP is a parameter representing the weight placed on the prior or base rate information. The generalized Bayes rule simplifies to the standard Bayes rule in the case when βL = βP = 1. Grether used the data from his experiment to estimate the weighting parameters, finding that βP = 1.82 and βL = 2.25. Thus, variation in the likelihood has a substantially larger influence on decisions than the variation in the prior, but the prior is not entirely ignored. Participants initially favored the likelihood just slightly more than those who had been through several trials of the experiment and thus had developed some experience. Thus, the data seem to confirm the notion of base rate neglect.

|
|
|
|
|
166 |
|
REPRESENTATIVENESS AND AVAILABILITY |
Base rate neglect can lead to biased decision making. For example, a short streak of declines in the stock indices often leads quickly to talk of a recession or a bear market. Nonetheless, bear markets are relatively rare and thus have a relatively low base rate. More often than not, a string of down days is simply a short-term chance event. Nonetheless, a string of down days is more representative of a bear market than a bull market. Here, base rate neglect could potentially drive investment decisions, leading people to jump to conclusions too early.
Base rate bias is only one example of how a representativeness heuristic can affect beliefs. In general, representativeness leads people to inflate their belief regarding the probability of events that resemble the data available. This can lead to several biases that are similar in nature to base rate neglect but that might not involve base rates at all. Several examples will be helpful in developing an understanding of how representativeness can affect beliefs and eventual decision making.
EXAMPLE 7.3 Linda
Consider the following question from Amos Tversky and Daniel Kahneman.
Linda is 31 years old, single, outspoken, and very bright. She majored in philosophy. As a student she was deeply concerned with issues of discrimination and social justice, and she also participated in antinuclear demonstrations.
Please rank the following statements by their probability, using 1 for the most probable and 8 for the least probable:
(a)Linda is a teacher in an elementary school.
(b)Linda works in a bookstore and takes yoga classes.
(c)Linda is active in the feminist movement.
(d)Linda is a psychiatric social worker.
(e)Linda is a member of the League of Women Voters.
(f)Linda is a bank teller.
(g)Linda sells insurance.
(h)Linda is a bank teller and is active in the feminist movement.
When participants in a psychological experiment responded to this question, the average rank of item (c) was 2.1; thus people believed it was very probable that Linda would be active in the feminist movement. The average rank of item (f) was 6.2 and was considered to be a relatively improbable event. But the rank of item (h) was 4.1, somewhere in between. Note that item (h) is the intersection of (c) and (f). Clearly, it must be less probable that Linda is both a bank teller and active in the feminist movement than that she is a bank teller at all. If it were not possible to be a bank teller and avoid being active in the feminist movement, these events should have equal probability and would thus be tied. If it is possible that she could be one and not the other, then the probability of being both must be smaller. In fact, around 90 percent of participants—even among those who have had several advanced courses in probability and statistics—ranked (h) as being more probable than (f).
