
- •Brief Contents
- •Contents
- •Preface
- •Who Should Use this Book
- •Philosophy
- •A Short Word on Experiments
- •Acknowledgments
- •Rational Choice Theory and Rational Modeling
- •Rationality and Demand Curves
- •Bounded Rationality and Model Types
- •References
- •Rational Choice with Fixed and Marginal Costs
- •Fixed versus Sunk Costs
- •The Sunk Cost Fallacy
- •Theory and Reactions to Sunk Cost
- •History and Notes
- •Rational Explanations for the Sunk Cost Fallacy
- •Transaction Utility and Flat-Rate Bias
- •Procedural Explanations for Flat-Rate Bias
- •Rational Explanations for Flat-Rate Bias
- •History and Notes
- •Theory and Reference-Dependent Preferences
- •Rational Choice with Income from Varying Sources
- •The Theory of Mental Accounting
- •Budgeting and Consumption Bundles
- •Accounts, Integrating, or Segregating
- •Payment Decoupling, Prepurchase, and Credit Card Purchases
- •Investments and Opening and Closing Accounts
- •Reference Points and Indifference Curves
- •Rational Choice, Temptation and Gifts versus Cash
- •Budgets, Accounts, Temptation, and Gifts
- •Rational Choice over Time
- •References
- •Rational Choice and Default Options
- •Rational Explanations of the Status Quo Bias
- •History and Notes
- •Reference Points, Indifference Curves, and the Consumer Problem
- •An Evolutionary Explanation for Loss Aversion
- •Rational Choice and Getting and Giving Up Goods
- •Loss Aversion and the Endowment Effect
- •Rational Explanations for the Endowment Effect
- •History and Notes
- •Thought Questions
- •Rational Bidding in Auctions
- •Procedural Explanations for Overbidding
- •Levels of Rationality
- •Bidding Heuristics and Transparency
- •Rational Bidding under Dutch and First-Price Auctions
- •History and Notes
- •Rational Prices in English, Dutch, and First-Price Auctions
- •Auction with Uncertainty
- •Rational Bidding under Uncertainty
- •History and Notes
- •References
- •Multiple Rational Choice with Certainty and Uncertainty
- •The Portfolio Problem
- •Narrow versus Broad Bracketing
- •Bracketing the Portfolio Problem
- •More than the Sum of Its Parts
- •The Utility Function and Risk Aversion
- •Bracketing and Variety
- •Rational Bracketing for Variety
- •Changing Preferences, Adding Up, and Choice Bracketing
- •Addiction and Melioration
- •Narrow Bracketing and Motivation
- •Behavioral Bracketing
- •History and Notes
- •Rational Explanations for Bracketing Behavior
- •Statistical Inference and Information
- •Calibration Exercises
- •Representativeness
- •Conjunction Bias
- •The Law of Small Numbers
- •Conservatism versus Representativeness
- •Availability Heuristic
- •Bias, Bigotry, and Availability
- •History and Notes
- •References
- •Rational Information Search
- •Risk Aversion and Production
- •Self-Serving Bias
- •Is Bad Information Bad?
- •History and Notes
- •Thought Questions
- •Rational Decision under Risk
- •Independence and Rational Decision under Risk
- •Allowing Violations of Independence
- •The Shape of Indifference Curves
- •Evidence on the Shape of Probability Weights
- •Probability Weights without Preferences for the Inferior
- •History and Notes
- •Thought Questions
- •Risk Aversion, Risk Loving, and Loss Aversion
- •Prospect Theory
- •Prospect Theory and Indifference Curves
- •Does Prospect Theory Solve the Whole Problem?
- •Prospect Theory and Risk Aversion in Small Gambles
- •History and Notes
- •References
- •The Standard Models of Intertemporal Choice
- •Making Decisions for Our Future Self
- •Projection Bias and Addiction
- •The Role of Emotions and Visceral Factors in Choice
- •Modeling the Hot–Cold Empathy Gap
- •Hindsight Bias and the Curse of Knowledge
- •History and Notes
- •Thought Questions
- •The Fully Additive Model
- •Discounting in Continuous Time
- •Why Would Discounting Be Stable?
- •Naïve Hyperbolic Discounting
- •Naïve Quasi-Hyperbolic Discounting
- •The Common Difference Effect
- •The Absolute Magnitude Effect
- •History and Notes
- •References
- •Rationality and the Possibility of Committing
- •Commitment under Time Inconsistency
- •Choosing When to Do It
- •Of Sophisticates and Naïfs
- •Uncommitting
- •History and Notes
- •Thought Questions
- •Rationality and Altruism
- •Public Goods Provision and Altruistic Behavior
- •History and Notes
- •Thought Questions
- •Inequity Aversion
- •Holding Firms Accountable in a Competitive Marketplace
- •Fairness
- •Kindness Functions
- •Psychological Games
- •History and Notes
- •References
- •Of Trust and Trustworthiness
- •Trust in the Marketplace
- •Trust and Distrust
- •Reciprocity
- •History and Notes
- •References
- •Glossary
- •Index

|
|
|
|
|
324 |
|
NAÏVE PROCRASTINATION |
behave better in the future, but that future is never realized. In this case, food stamp recipients believe they will be able to restrain their appetites later in the month, but they never do. This eventually leads to severe shortages of food in the last week, as the data have documented. Often, hyperbolic discounting is misunderstood to simply embody heavy discounting of the future. Instead, it is a statement on how discounting of a pair of days in the future evolves as those days become closer to the present and how this causes recipients to change their consumption plans.
Naïve Quasi-Hyperbolic Discounting
One of the primary advantages of the exponential discounting function is the simplicity with which the exponential discount could be used in solving maximization problems. By contrast, the hyperbolic discounting model can be difficult to deal with mathematically given the functional form for the discount factor. This has led David Laibson to propose an approximation to the hyperbolic discounting function called quasi-hyper- bolic discounting.
Quasi-hyperbolic discounting separates the hyperbolic profile of time discounting into two different discount factors. These two factors represent the discount applied to utility of consumption in the second period and the discount applied to the utility of consumption for each additional period, respectively. The discount factor applied to the second period is small relative to the other discount factor, representing the notion that people discount consumption tomorrow relative to today more heavily than the day after tomorrow relative to tomorrow. In other words, any consumption in the future receives some penalty in the mind of the consumer, but trading off consumption between two different periods in the future does not face such a steep penalty. Thus, instead of the model in equation 12.2, we write
U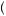 c1, c2,
c1, c2, 


 =u
=u c1
c1 +βu
+βu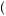 c2
c2 +βδu
+βδu c3
c3 +βδ2u
+βδ2u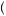 c4
c4 + +βδi−2u
+ +βδi−2u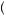 ci
ci +
+
|
T |
12 30 |
=βu c1 + |
βδi−2u ci , |
|
|
i =2 |
|
where 0 < β < δ < 1, and where, if we want to consider the infinite time horizon problem, T may be  . Here β represents the discount applied to utility of consumption in the second period (which also multiplies utility in all future periods), and δ represents the discount applied to utility of consumption for each additional period as we move farther into the future. In general, if β < δ the function approximates hyberbolic discounting.
. Here β represents the discount applied to utility of consumption in the second period (which also multiplies utility in all future periods), and δ represents the discount applied to utility of consumption for each additional period as we move farther into the future. In general, if β < δ the function approximates hyberbolic discounting.
Figure 12.4 displays a quasi-hyperbolic discounting function (marked in triangles) that has been selected to approximate the corresponding hyperbolic discounting function. The advantage of this form is that it closely replicates the exponential mathematical form, thus restoring the simple mathematical formulas for time-discounting problems. The solution to the utility-maximization problem for equation 12.30 again requires that discounted marginal utility is equal. However, the differential discount implies
u′ c1 = βδi − 2u′ ci |
12 31 |

|
|
|
|
|
Naïve Quasi-Hyperbolic Discounting |
|
325 |
|
|
and for i, j > 1 |
|
|
|
|
u′ ci = δj − iu′ cj . |
12 32 |
|
|
|
Both of these equations are reminiscent of equation 12.18. Thus, given a functional form for the instantaneous utility function, we can find a relationship between planned consumption in one period and the next.
For example, suppose that people must maximize their utility of consumption over an infinite time horizon, given an initial endowment of wealth w. Suppose further that u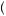 c
c = cα, so that the marginal utility (or slope of the utility function) of consumption is
= cα, so that the marginal utility (or slope of the utility function) of consumption is
given by u′ c = αcα − 1. Then equations 12.31 and 12.32 imply |
|
|
|
||||||||||||||||||||||||||||||
αc1α − 1 = αβc2α − 1 = αβδc3α − 1 = |
|
|
|
|
|
= αβδi − 2ciα − 1 = |
|
12 33 |
|
||||||||||||||||||||||||
or |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
1 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
αβδi − 2 |
1 |
|
|
|
|
|
|
||||||||
α |
α − 1 |
c1 = |
αβ |
|
α − 1 |
c2 = |
= |
|
α − 1ci = |
. |
12 34 |
|
|||||||||||||||||||||
This implies that c2 = c1β − |
1 |
|
, and that in general ci = c1β − |
1 |
δ − |
i − 2 |
when i = 2, 3, |
. |
|||||||||||||||||||||||||
α − |
1 |
α − 1 |
α − 1 |
||||||||||||||||||||||||||||||
The budget constraint implies |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
c1 + c2 + c3 + = w, |
|
|
|
|
|
12 35 |
|
|||||||||||||||||||||
or, substituting from above, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
c1 |
1 + β − |
1 |
|
|
|
|
|
|
|
|
|
δ − |
1 |
i |
= w. |
|
12 36 |
|
|||||||||||||
|
|
α − 1 |
i = 0 |
α − 1 |
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
By the properties of geometric series,2 this can be rewritten as |
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
β − |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
c1 |
1 + |
|
|
α − |
1 |
|
|
|
|
|
= w, |
|
|
|
|
|
12 37 |
|
||||||||||
|
|
|
|
|
|
|
− δ − |
1 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
α − 1 |
|
|
|
|
|
|
|
||||||||||||||||||||
leading to the closed-form solution |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
c1 = |
|
|
|
|
|
w |
|
|
|
|
|
|
|
. |
|
|
|
|
|
12 38 |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
β − |
1 |
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
1 + |
|
|
α − 1 |
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
− δ |
− |
α − 1 |
|
|
|
|
|
|
|
|
|||||||||
All other periods’ consumption could then be calculated from the above formula via equation 12.34.
2 Let Y = k + kr + kr2 + kr3 + |
= |
krt , where |
0 < r < 1. Then, Y = k 1 − r . To see this, note that |
||||
|
|
|
|
|
|
t = 0 |
|
Y = k + kr + kr2 + kr3 + . Also, rY = kr + kr2 + kr3 + |
. Thus, Y − rY = k, or Y 1 − r = k implying the result. In |
||||||
this case, k = β − |
1 |
, and r = δ − |
1 |
|
. |
|
|
α − 1 |
α − |
1 |
|
|
|||

|
|
|
|
|
|
|
|
|
326 |
|
NAÏVE PROCRASTINATION |
|
|
|
|
|
|
|
Table 12.2 Estimated Discount Factors for Different Amounts |
|
|||
|
|
|
and Lengths of Time |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Time Delay |
|
|
|
|
|
|
|
|
|
|
|
|
Amount |
6 Months |
1 Year |
2 Years |
4 Years |
|
|
|
|
|
|
|
|
|
|
|
$40 |
0.626 |
0.769 |
0.792 |
0.834 |
|
|
|
$200 |
0.700 |
0.797 |
0.819 |
0.850 |
|
|
|
$1,000 |
0.710 |
0.817 |
0.875 |
0.842 |
|
|
|
$5,000 |
0.845 |
0.855 |
0.865 |
0.907 |
|
|
|
|
|
|
|
|
Source: Benzion, U., A. Rapoport, and J. Yagil. ”Discount Rates Inferred from Decisions: An Experimental Study.“
Management Science 35(1989): 270–284.
Alternatively, if we modeled the same decision using a hyperbolic discount function, equation 12.36 would be replaced by
|
− β |
|
c1 1 + |
1 + iα α = w, |
12 39 |
|
i = 1 |
|
which cannot yield a closed-form solution. Thus, in many situations, economists use the quasi-hyperbolic approximation rather than the hyperbolic form. In fact, the quasihyperbolic form is much more common in practice than the hyperbolic form that it approximates.
Uri Benzion, Amnon Rapoport, and Joseph Yagil find evidence of changing discount rates over time. They asked 204 participants about their preferences between receiving bundles of money after various waiting periods. For example, one question asks participants to suppose they had just earned $200 for their labors, but after coming to pick up the money, they find their employer is temporarily out of funds. Instead, they are offered payment in six months. Participants were asked how much would need to be paid at the later time to be indifferent between receiving $200 now or the higher amount later. The amounts of money and the length of time were varied. Table 12.2 displays the estimated discount factors for each of the various scenarios similar to the scenario just described, assuming a money metric utility function.3 For each, we see a relatively large discount factor for the first six months of delay. Discounts for longer periods are much smaller, reflecting the hyperbolic nature of discounting. If a person must delay a reward for some time, longer waits are no longer thought of as so costly. Similar experiments have been run with actual money payouts, finding additional evidence that discount factors climb over time, eventually becoming stable.
3 They actually calculate average discount rate. This is the rate R such that F = P(1+R)t, where P is the present amount, and F is the future amount. The discount factor that we have discussed in this chapter is equivalent to δ = 1/ (1+R). The table displays the discount factor implied by the discount rate they report. The money metric utility function simply assumes that utility is linear in dollars.

|
|
|
|
Naïve Quasi-Hyperbolic Discounting |
|
327 |
|
 EXAMPLE 12.2 Reading Days Are for Procrastination
EXAMPLE 12.2 Reading Days Are for Procrastination
It seems to have happened to all of us at one time or another. In fact, many of us have experienced it repeatedly. The big test is coming in two weeks, and we should be studying. But there is so much time before that. “I could put off studying one more day without hurting my grade,” you may tell yourself. Each day you tell yourself this, until it is so late that you truly do not have as much time to study as you probably should have. Your grade is not what you wanted or what you could have achieved. Then the next semester, despite your previous experience, you procrastinate just as before.
Hyperbolic discounting might provide one explanation for why procrastination is so prevalent. Consider a student with the following (daily) instantaneous utility function
u s = − s2, |
12 40 |
where s is the portion of the day spent studying. Thus, one receives negative instantaneous utility from studying, with decreasing marginal pain from additional studying given by u′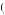 s
s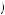 = − 2s. Moreover, suppose that the grade on a particular test is measured by an index g, as a function of time studying:
= − 2s. Moreover, suppose that the grade on a particular test is measured by an index g, as a function of time studying:
g s = s. |
12 41 |
Of course it is more likely that grades show declining returns to studying, but this abstraction makes our example easier to calculate, and it ensures a solution will exist. Finally, suppose that the student’s utility of receiving a grade of g is equal to g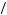 2, discounted as if received on the day the results are announced. Finally, suppose that the student discounts future utility according to a quasi-hyperbolic discount function.
2, discounted as if received on the day the results are announced. Finally, suppose that the student discounts future utility according to a quasi-hyperbolic discount function.
Suppose further that the exam will take place in four days, and the results will be announced seven days later. The student has set a goal of studying a total of 1.05 days. For simplicity, consider that the student is choosing between two different study plans. The first plan consists of s1 =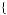 0.21, 0.21, 0.21, 0.21, 0.21
0.21, 0.21, 0.21, 0.21, 0.21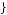 , indicating that the student will study 0.21 of a day each day until the test. The second plan considers shirking today,
, indicating that the student will study 0.21 of a day each day until the test. The second plan considers shirking today,
but making up for it later, s′ = 0.17, 0.22, 0.22, 0.22, 0.22 . These plans are not
1
binding, meaning that the student could easily change her mind tomorrow. If s is chosen,
the student obtains a negative instantaneous utility of |
0.21 2 = − 0.0441 today and |
||
each of the next four days. Then, seven days later, |
she will receive a grade of |
||
0.21 × 5 = 1.05, yielding instantaneous utility 0.525. This can be written |
|
||
|
5 |
|
|
U s1 = − 0.0441 − |
i = 2 βδi − 2 × 0.0441 |
+ βδ10 × 0.525. |
12 42 |
So, for example, if β = 0.75 and δ = 0.99, then U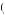 s1
s1
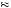 0.182. Alternatively, if s′ is chosen, then instantaneous utility in the first day will be
0.182. Alternatively, if s′ is chosen, then instantaneous utility in the first day will be  0.17
0.17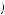 2 = − 0.0289, and instantaneous utility on each succeeding day will be
2 = − 0.0289, and instantaneous utility on each succeeding day will be  0.22
0.22 2 = 0.0484. Moreover, the grade will be 0.17 + 4 × 0.22 = 1.05, yielding instantaneous utility 0.525:
2 = 0.0484. Moreover, the grade will be 0.17 + 4 × 0.22 = 1.05, yielding instantaneous utility 0.525:
′ |
= − 0.0289 − |
5 |
|
i − 2 |
10 |
× 0.525. |
12 43 |
U s1 |
i = 2 |
βδ |
|
× 0.0484 + βδ |

|
|
|
|
|
|
|
|
|
|
|
|
328 |
|
NAÏVE PROCRASTINATION |
|
|
|
|
|
|
|
|
|
Thus, if β = 0.75 and δ = 0.99, then U s1′ |
0.184, and the student will plan on s′, |
|||||||
|
|
shirking somewhat today and planning to make up the time with extra studying |
||||||||
|
|
tomorrow. |
|
|
|
|
|
|
|
|
|
|
|
The next day, however, the student needs to choose again how much to study. In this |
|||||||
|
|
case, with only four days in which to study, suppose the choice is between sticking to the |
||||||||
|
|
plan s2′ = 0.22, 0.22, 0.22, 0.22 |
or shirking somewhat today and making it up with |
|||||||
|
|
more time studying later s2 |
= 0.19, 0.23, 0.23, 0.23 , where again both plans yield the |
|||||||
|
|
|
″ |
|
|
|
|
|
|
|
|
|
target amount of studying, 1.05. In this case, sticking to the plan would yield |
|
|||||||
|
|
|
′ |
4 |
i − 2 |
× 0.0484 + βδ |
9 |
× 0.525 0.145. |
12 44 |
|
|
|
|
U s2 = − 0.0484 − |
i = 2 |
βδ |
|
||||
Choosing to procrastinate yields instantaneous utility of 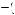 0.19
0.19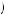 2 = 0.0361 in the first period and
2 = 0.0361 in the first period and 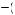 0.23
0.23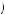 2 = 0.0529 in the three following periods. The grade obtained will be 0.17 + 0.19 + 3 × 0.23 = 1.05, yielding instantaneous utility of 0.525 when the grades are received, or
2 = 0.0529 in the three following periods. The grade obtained will be 0.17 + 0.19 + 3 × 0.23 = 1.05, yielding instantaneous utility of 0.525 when the grades are received, or
″ |
= − 0.0361 − |
4 |
i − 2 |
× 0.0529 + βδ |
9 |
× 0.525 0.147. |
12 45 |
U s2 |
i = 2 |
βδ |
|
Thus, the student decides again to postpone the bulk of her studying.
Similar choices each day lead the student to postpone studying, planning to eventually make up the time and obtain the same grade. The next day, the student decides
whether to continue with her new plan s″ = 0.23, 0.23, 0.23 , yielding utility
3
″ |
= − 0.0529 − |
3 |
i − 2 |
× 0.0529 + |
|
8 |
× 0.525 |
0.107, |
12 46 |
|
U s3 |
i = 2 |
βδ |
|
βδ |
|
|||||
or to procrastinate again by planning on s3 = 0.21, 0.24, 0.24 |
and yielding utility |
|||||||||
|
|
|
|
|
′″ |
|
|
|
|
|
′″ |
= − 0.0441 − |
3 |
|
i − 2 |
|
|
8 |
|
|
|
U s 3 |
i = 2 |
βδ |
|
× 0.0576 + βδ |
× 0.525 |
0.109, |
12 47 |
|||
where again the planned grade is 1.05. She again chooses to procrastinate and in the
fourth day faces the |
choice of |
continuing |
with |
s 4 = 0.24, 0.24 , |
with U s 4 = |
||
|
|
7 |
|
|
|
′″ |
′″ |
− 0.0576 − β0.0576 + βδ |
0.067 |
or |
|
″″ |
= 0.23, 0.25 , |
||
× 0.525 |
procrastinating with s4 |
||||||
″″ |
|
|
7 |
× 0.525 |
0.068. In this fourth day she also |
||
yielding U s4 |
= − 0.0529 − β0.0625 + βδ |
||||||
chooses to procrastinate. In the final day, the student faces the choice to study according
to plan s5 = 0.25 |
, yielding U s5 |
0.026, or to just give up, s5 |
= 0.16 , yielding |
|
U s5 |
″″ |
″″ |
′″″ |
|
0.031. |
|
|
|
|
′″″ |
|
|
|
|
The student eventually has an actual study profile of 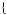 0.17, 0.19, 0.21, 0.25, 0.16
0.17, 0.19, 0.21, 0.25, 0.16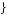 , yielding a grade of 1, less than the grade planned upon in each of the prior periods. The student’s procrastination ends up costing her almost 20 percent of the anticipated grade on the test. This is the cost of not recognizing that as the test moves closer, she will change the way she discounts between the days of the study period. For the first four days of the study period, she believes she will trade off the disutility of studying between day 4 and day 5 by δ. By the time day 4 rolls around, she instead discounts day 5 disutility of studying by β. It is the constant shifting of the β discount through time that explains the procrastination behavior.
, yielding a grade of 1, less than the grade planned upon in each of the prior periods. The student’s procrastination ends up costing her almost 20 percent of the anticipated grade on the test. This is the cost of not recognizing that as the test moves closer, she will change the way she discounts between the days of the study period. For the first four days of the study period, she believes she will trade off the disutility of studying between day 4 and day 5 by δ. By the time day 4 rolls around, she instead discounts day 5 disutility of studying by β. It is the constant shifting of the β discount through time that explains the procrastination behavior.

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Naïve Quasi-Hyperbolic Discounting |
|
329 |
|
||||||||
|
EXAMPLE 12.3 |
Going on a Diet |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
Obesity has become a major issue around the world, and particularly in the United |
|
|
||||||||||||||||||||||||||||||
States. Some economists have placed the annual economic cost of obesity and over- |
|
|
||||||||||||||||||||||||||||||
weight at around $500 billion. Almost 60 percent of Americans want to lose weight, but |
|
|
||||||||||||||||||||||||||||||
only about 15 percent are on a weight-loss diet at any time. |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
Put yourself in their shoes. Suppose you are overweight and want to go on a diet. Yet |
|
|
|||||||||||||||||||||||||||||
every day you face the choice to eat food you like, xl, that will likely maintain your high |
|
|
||||||||||||||||||||||||||||||
weight, or to eat food that is healthy, xh, which you do not like as much, and potentially |
|
|
||||||||||||||||||||||||||||||
lose weight. Let us suppose that people derive their utility from eating food and from |
|
|
||||||||||||||||||||||||||||||
their weight and that the instantaneous utility of each is additively separable. Thus, |
|
|
||||||||||||||||||||||||||||||
utility at time t, can be represented as u xt , wt |
= ux xt |
+ uw |
|
wt , where xt |
is food |
|
|
|||||||||||||||||||||||||
consumption at time t, ux x is utility of food consumption, wt is weight at time t, and |
|
|
||||||||||||||||||||||||||||||
uw w |
is utility of weight. Suppose that eating what you like provides an instantaneous |
|
|
|||||||||||||||||||||||||||||
utility |
of ux xl = ul, |
which |
|
is |
larger |
than the utility of eating |
food that is |
healthy, |
|
|
||||||||||||||||||||||
ux xh |
= uh. Weight takes a long time to change. Let us suppose that weight is the result |
|
|
|||||||||||||||||||||||||||||
of a weighted sum of consumption over the last 180 days, wt = |
|
t − 1 |
|
|
|
|
|
|
||||||||||||||||||||||||
|
i = t − 180 γixi , and that |
|
|
|||||||||||||||||||||||||||||
people receive instantaneous utility of weight according to u w = − |
|
− w 2, where |
|
|
|
|
|
|||||||||||||||||||||||||
w |
w |
|
|
|||||||||||||||||||||||||||||
is the person’s ideal weight. Thus, any deviation from this ideal induces a lower utility. At |
|
|
||||||||||||||||||||||||||||||
any point in time the potential dieter faces the decision (placing this in the framework of |
|
|
||||||||||||||||||||||||||||||
an infinite planning horizon problem) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
max |
xt t = |
|
u x |
1 |
, |
w |
+ β |
δt − 2u x |
, w . |
|
|
|
12 48 |
|
|
|
|
||||||||||||
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
1 |
t = 2 |
t |
t |
|
|
|
|
|
|
|
|
|
|
||||
|
Let’s begin by ignoring the current period and considering behavior in the next |
|
|
|||||||||||||||||||||||||||||
period. In that period, people could choose either to eat what they like or to eat healthy |
|
|
||||||||||||||||||||||||||||||
food. If they choose to eat healthy food in the next period, they will obtain |
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
u x1, w1 + βuh − |
|
− w2 |
2 + β |
t = 3 δt − 2u xt , wt x2 = xh . |
12 49 |
|
|
|
|
|||||||||||||||||||||
|
|
w |
|
|
|
|||||||||||||||||||||||||||
If instead they choose not to eat healthy food in the next period, they will obtain |
|
|
||||||||||||||||||||||||||||||
|
|
u x1, w1 + βul − |
|
|
|
− w2 |
2 + β |
t = 3 δt − 2u xt , wt x2 = xl . |
12 50 |
|
|
|
|
|||||||||||||||||||
|
|
w |
|
|
|
|||||||||||||||||||||||||||
They will thus plan to eat healthy food in the next period if |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
uh − |
t = 3 δt − 2 |
|
|
|
|
− |
t − 1 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
w |
i = t − 180 |
γixi x2 = xh |
> ul |
12 51 |
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t − 1 |
|
2 |
|
|
|
|
|
|
|
|
||
|
|
|
− |
t = 3 δt − 2 |
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
w |
i = t − 180 |
γixi x2 = xl |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
or if the instantaneous difference in utility of consumption is smaller than the discounted |
|
|
||||||||||||||||||||||||||||||
difference in utility of weight: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
t − 2 |
|
|
|
|
|
|
|
|
|
|
|
t − 1 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
t = 3 δ |
|
w − |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
i = t − 180 γixi x2 = xl |
> ul − uh. |
12 52 |
|
|
|
|
||||||||||||||||
|
|
− |
|
|
t − 2 |
|
|
|
|
|
|
− |
|
|
t − 1 |
|
2 |
|
|
|
|
|||||||||||
|
|
t = 3 δ |
|
|
w |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
i = t − 180 γixi x2 = xh |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
