
- •Brief Contents
- •Contents
- •Preface
- •Who Should Use this Book
- •Philosophy
- •A Short Word on Experiments
- •Acknowledgments
- •Rational Choice Theory and Rational Modeling
- •Rationality and Demand Curves
- •Bounded Rationality and Model Types
- •References
- •Rational Choice with Fixed and Marginal Costs
- •Fixed versus Sunk Costs
- •The Sunk Cost Fallacy
- •Theory and Reactions to Sunk Cost
- •History and Notes
- •Rational Explanations for the Sunk Cost Fallacy
- •Transaction Utility and Flat-Rate Bias
- •Procedural Explanations for Flat-Rate Bias
- •Rational Explanations for Flat-Rate Bias
- •History and Notes
- •Theory and Reference-Dependent Preferences
- •Rational Choice with Income from Varying Sources
- •The Theory of Mental Accounting
- •Budgeting and Consumption Bundles
- •Accounts, Integrating, or Segregating
- •Payment Decoupling, Prepurchase, and Credit Card Purchases
- •Investments and Opening and Closing Accounts
- •Reference Points and Indifference Curves
- •Rational Choice, Temptation and Gifts versus Cash
- •Budgets, Accounts, Temptation, and Gifts
- •Rational Choice over Time
- •References
- •Rational Choice and Default Options
- •Rational Explanations of the Status Quo Bias
- •History and Notes
- •Reference Points, Indifference Curves, and the Consumer Problem
- •An Evolutionary Explanation for Loss Aversion
- •Rational Choice and Getting and Giving Up Goods
- •Loss Aversion and the Endowment Effect
- •Rational Explanations for the Endowment Effect
- •History and Notes
- •Thought Questions
- •Rational Bidding in Auctions
- •Procedural Explanations for Overbidding
- •Levels of Rationality
- •Bidding Heuristics and Transparency
- •Rational Bidding under Dutch and First-Price Auctions
- •History and Notes
- •Rational Prices in English, Dutch, and First-Price Auctions
- •Auction with Uncertainty
- •Rational Bidding under Uncertainty
- •History and Notes
- •References
- •Multiple Rational Choice with Certainty and Uncertainty
- •The Portfolio Problem
- •Narrow versus Broad Bracketing
- •Bracketing the Portfolio Problem
- •More than the Sum of Its Parts
- •The Utility Function and Risk Aversion
- •Bracketing and Variety
- •Rational Bracketing for Variety
- •Changing Preferences, Adding Up, and Choice Bracketing
- •Addiction and Melioration
- •Narrow Bracketing and Motivation
- •Behavioral Bracketing
- •History and Notes
- •Rational Explanations for Bracketing Behavior
- •Statistical Inference and Information
- •Calibration Exercises
- •Representativeness
- •Conjunction Bias
- •The Law of Small Numbers
- •Conservatism versus Representativeness
- •Availability Heuristic
- •Bias, Bigotry, and Availability
- •History and Notes
- •References
- •Rational Information Search
- •Risk Aversion and Production
- •Self-Serving Bias
- •Is Bad Information Bad?
- •History and Notes
- •Thought Questions
- •Rational Decision under Risk
- •Independence and Rational Decision under Risk
- •Allowing Violations of Independence
- •The Shape of Indifference Curves
- •Evidence on the Shape of Probability Weights
- •Probability Weights without Preferences for the Inferior
- •History and Notes
- •Thought Questions
- •Risk Aversion, Risk Loving, and Loss Aversion
- •Prospect Theory
- •Prospect Theory and Indifference Curves
- •Does Prospect Theory Solve the Whole Problem?
- •Prospect Theory and Risk Aversion in Small Gambles
- •History and Notes
- •References
- •The Standard Models of Intertemporal Choice
- •Making Decisions for Our Future Self
- •Projection Bias and Addiction
- •The Role of Emotions and Visceral Factors in Choice
- •Modeling the Hot–Cold Empathy Gap
- •Hindsight Bias and the Curse of Knowledge
- •History and Notes
- •Thought Questions
- •The Fully Additive Model
- •Discounting in Continuous Time
- •Why Would Discounting Be Stable?
- •Naïve Hyperbolic Discounting
- •Naïve Quasi-Hyperbolic Discounting
- •The Common Difference Effect
- •The Absolute Magnitude Effect
- •History and Notes
- •References
- •Rationality and the Possibility of Committing
- •Commitment under Time Inconsistency
- •Choosing When to Do It
- •Of Sophisticates and Naïfs
- •Uncommitting
- •History and Notes
- •Thought Questions
- •Rationality and Altruism
- •Public Goods Provision and Altruistic Behavior
- •History and Notes
- •Thought Questions
- •Inequity Aversion
- •Holding Firms Accountable in a Competitive Marketplace
- •Fairness
- •Kindness Functions
- •Psychological Games
- •History and Notes
- •References
- •Of Trust and Trustworthiness
- •Trust in the Marketplace
- •Trust and Distrust
- •Reciprocity
- •History and Notes
- •References
- •Glossary
- •Index

|
|
|
|
|
226 |
|
DECISION UNDER RISK AND UNCERTAINTY |
lottery is a postal code lottery. In this lottery, players either buy a ticket or not. The number is the postal code in which they reside. If their postal code is selected, they win. However, if they don’t buy and their postal code is selected, many of their neighbors win and they don’t. Such an outcome could induce regret for not having purchased a lottery ticket. Alternatively, not playing the standard lottery generally means you did not have a selected number in mind and thus would never know that you would have won had you simply bought a ticket.
Marcel Zeelenberg and Rik Pieters surveyed potential lottery players in the Netherlands regarding the two lotteries. A larger percentage associated feelings of regret with the postal code lottery than with the standard lottery. Moreover, these anticipated feelings of regret influenced people’s intentions to buy lottery tickets. The more regret they anticipated due to knowing they had lost, the more likely they were to play the postal code lottery. Alternatively, regret had little to do with purchasing standard lottery tickets.
Chris Guthrie found similar sentiments when surveying law students about the potential to settle out of court rather than pursue trial. Going to trial is generally a risky proposition. Courts might decide in your favor and award you a substantial amount of money. Alternatively, they might decide against you, in which case you can incur significant court costs without compensation. In many cases, many plaintiffs sue for similar offenses. For example, several workers at a plant might sue for damages caused by unsafe working conditions. Each case should have the same chance of succeeding provided their lawyers have the same level of skill. In this case, a single worker might decide to settle out of court, but if others do not, they will likely learn of the potential outcome had they gone to court. Guthrie finds that law students believe litigants are more likely to settle out of court if they will likely never know what the outcome of the trial would be. This might mean that people in parallel cases are much less likely to settle, whereas combining their cases could lead them to avoid going to trial. Regret can push people to take much greater risk at substantial cost.
Independence and Rational Decision under Risk
Expected utility also requires that behavior conform to the independence axiom. This axiom provides a description of how people value compound gambles. A compound gamble is a gamble that consists of receiving some other set of gambles with fixed probabilities.
Independence Axiom
Let A, B, and C represent three gambles. If A 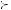 B, then the compound gamble that yields gamble A with probability p and gamble C with probability
B, then the compound gamble that yields gamble A with probability p and gamble C with probability 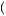 1 − p
1 − p is preferred to the compound gamble that yields B with probability p and C with probability
is preferred to the compound gamble that yields B with probability p and C with probability 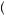 1 − p
1 − p , which can be written in shorthand form pA +
, which can be written in shorthand form pA + 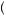 1 − p
1 − p C
C 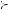 pB +
pB +  1 − p
1 − p C.
C.
The independence axiom imposes that preferences between two gambles should not be affected by common contingencies. Thus, if I prefer to bet $5 on the red horse rather

|
|
|
|
Independence and Rational Decision under Risk |
|
227 |
|
than the blue horse when they are the only two horses running, I should still prefer to bet on the red horse over the blue horse if a third (or even many more) horses are racing. Suppose that betting on the winning horse would double your money, but betting on any other horse would result in no payoff. Further, suppose there is 0.6 probability of the red horse beating the blue horse. Then betting on the red horse when they are the only two horses running (Gamble A) means taking a gamble that yields $10 with probability 0.6 and $0 with probability 0.4. Betting on the blue horse when only two horses are running (Gamble B) would yield $0 with 0.6 probability and $10 with 0.4 probability. Most would choose gamble A given it yields a higher probability of obtaining money. Now suppose a third horse (green horse) is also running. With all three, suppose that there is a 0.2 probability that the green horse will win, and the remaining 0.8 probability is distributed as before: 0.8 × 0.6 = 0.48 probability that red will win and 0.8 × 0.4 = 0.32 probability that blue will win. If given only the choice between betting on red or blue, the independence axiom requires that a bettor still prefers betting on red. In this case, Gamble C can be thought of as betting on either blue or red when green will win the race for certain. This results in a probability of 1 of receiving $0. Betting on red in the threehorse race is like taking the compound gamble that yields Gamble A with probability 0.8 and Gamble C with probability 0.2. Betting on blue in the three-horse race is like taking the compound gamble that yields Gamble B with probability 0.8 and Gamble C with probability 0.2.
One must be careful when applying the independence axiom to fully specify each gamble. For example, suppose we consider a man who has agreed to meet his spouse for an evening out. They had discussed on the phone either going to a movie or bowling, but the conversation was cut off before they had made a final decision. Thus, he must choose to go either to the bowling alley or to the movie theater with a chance that his spouse will choose to go to the other event. The man is indifferent between attending a movie or bowling by himself, but he would much prefer to be at an event with his spouse to attending alone. In this case, we might be tempted to say that if the husband is indifferent between going bowling with his spouse or to a movie with his spouse, u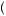 bowling, spouse
bowling, spouse = u
= u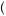 movie, spouse
movie, spouse , then the husband should also be indifferent among the following three gambles
, then the husband should also be indifferent among the following three gambles
Gamble A: |
Gamble B: |
Gamble C: |
Spouse attends movie with |
Spouse attends bowling |
0.5 probability spouse attends |
certainty |
with certainty |
movie |
|
|
0.5 probability spouse attends bowling |
|
|
|
However, this is not the case. In this case, we have not fully specified the gambles. If the man knows his spouse will be at the movie (Gamble A), he will choose to attend the movie and obtain a higher level of utility, u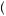 movie, spouse
movie, spouse . If the man knows his spouse will be at the bowling alley (Gamble B), he will attend also and obtain a higher utility, u
. If the man knows his spouse will be at the bowling alley (Gamble B), he will attend also and obtain a higher utility, u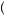 bowling, spouse
bowling, spouse . If instead, he believes Gamble C to be the case, whichever choice he
. If instead, he believes Gamble C to be the case, whichever choice he
takes (e.g., bowling) will |
result in a 0.5 probability of being there alone, yielding |
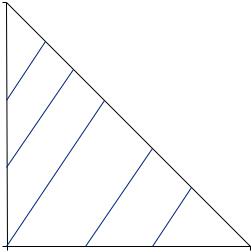
U = 0.5u bowling, spouse |
+ 0.5u bowling, alone < u bowling, spouse . In this case, |
the specification of the gambles does not allow for the person’s reaction. Suppose on the
|
|
|
|
|
228 |
|
DECISION UNDER RISK AND UNCERTAINTY |
way to his car, the man runs into his spouse, who promptly blindfolds him and drives him to one of the events. Now he is guaranteed to be there with his spouse, and he is indifferent between the movie and bowling. If we consider Gambles A, B, and C in the context of the man’s spouse choosing which event to go to, the independence axiom would now apply. Because he knows he will be there with his spouse, Gamble A will yield u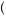 movie, spouse
movie, spouse and Gamble B will yield u
and Gamble B will yield u bowling, spouse
bowling, spouse . But in this case, if the spouse decides which event to attend by a simple coin flip (Gamble C), the husband will receive U = 0.5u
. But in this case, if the spouse decides which event to attend by a simple coin flip (Gamble C), the husband will receive U = 0.5u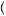 bowling, spouse
bowling, spouse + 0.5u
+ 0.5u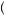 movie, spouse
movie, spouse = u
= u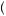 bowling, spouse
bowling, spouse . Thus, he doesn’t care where the spouse decides to drive him.
. Thus, he doesn’t care where the spouse decides to drive him.
The order axiom implies that we can represent the preferences of any degenerate gambles (gambles with only one possible outcome) using a utility function. Thus, we could define a function u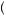 x
x , where x represents an amount of money obtained with certainty. The continuity and independence axioms tell us how this utility function must relate to the preferences for gambles involving risk. From continuity and independence, we know we can represent the utility of the combination of any two gambles as the sum of the probability of each gamble multiplied by the utility derived from each gamble, thus yielding the expected utility model.
, where x represents an amount of money obtained with certainty. The continuity and independence axioms tell us how this utility function must relate to the preferences for gambles involving risk. From continuity and independence, we know we can represent the utility of the combination of any two gambles as the sum of the probability of each gamble multiplied by the utility derived from each gamble, thus yielding the expected utility model.
Economists have generally embraced expected utility since its reintroduction by John von Neuman and Oskar Morgenstern in the 1940s in their work creating the field of game theory. The axioms upon which expected utility rests make sense as behavioral rules. It would be hard to argue that people wishing to make themselves the best off they can be would violate such a clear and logical set of rules. Nonetheless, these rationality axioms make some strict predictions about behavior and preferences.
One simple way to think about expected utility theory is in terms of indifference curves over gambles involving the same outcomes but different probabilities of those outcomes. Figure 9.2 displays indifference curves over three outcomes in a display alternatively referred to as the unit simplex or the Marschak–Machina triangle (after
p(100) = 1 Eu(x) = u(100)
|
Probability of $100 |
FIGURE 9.2 |
|
Indifference Curves |
|
over Compound |
|
Gambles involving |
p(100) = 0 |
$100, $50, and $0 |
p(0) = 0 |
Eu(x) = u(50)
|
Eu(x) = u(0) |
Probability of $0 |
p(0) = 1 |
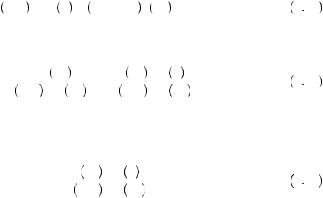
|
|
|
|
Independence and Rational Decision under Risk |
|
229 |
|
Jacob Marschak and Mark Machina). The x-axis in the figure represents the probability of wining $0, and the y-axis represents the probability of winning $100. The probability of a third outcome, winning $50, is not pictured on an axis. Thus, each point in the triangle represents a lottery with the probability of winning $0 represented by the x- coordinate, the probability of winning $100 represented by the y-coordinate, and the probability of winning $50 equal to the remaining probability (one minus the x- and y- coordinates). The points along the x-axis represent gambles in which the probability of winning $100 is 0. Thus all points on this line represent gambles that could result in winning either $50 or $0. The point (0,0) represents the gamble yielding $50 with certainty. The point (1,0) represents winning $0 with certainty. The points along the y- axis represent all gambles with a probability of 0 of winning $0. The point (0,1) represents the gamble that yields $100 with certainty. The dashed line running from the upper left to the lower right portion of the graph represents the boundary of the triangle. Along this boundary the sum of probabilities of $100 and $0 outcomes is 1, and thus the probability of winning $50 is 0.
The parallel lines stretching from the lower left to the upper right represent indifference curves in the triangle. The indifference curve containing all points yielding utility identical to receiving $50 with certainty is labeled. Because we have placed the probability of $100 on the y-axis and $0 on the x-axis, all indifference curves to the left of this curve represent a higher level of utility than $50 and all to the right represent a lower level of utility. You will note that all indifference curves are parallel and straight lines. Let y be the probability of winning $100 and x be the probability of winning $0. In the triangle, an indifference curve is all probabilities y and x that satisfy
yu 100 + xu 0 + 1 − x − y u 50 = k. |
9 14 |
Solving equation 9.14 for y in terms of x yields
y = |
k − u 50 |
+ x |
u 50 |
− u 0 |
. |
9 15 |
|
|
|
||||
u 100 − u 50 |
u 100 |
− u 50 |
|
|||
Because the value k and the utilities are fixed, this always represents a line with slope given by
y |
= |
u 50 |
− u 0 |
. |
9 16 |
|
u 100 |
|
|||
x |
− u 50 |
|
|||
Thus, expected utility theory implies that all indifference curves must be straight lines, with each having the identical slope. This property drives many of the tests of expected utility theory.
Note that the slope of the line in equation 9.15 is made up of the ratio of the difference in utility between $50 and $0 to the difference in utility between $100 and $50. Recall from Chapter 6, that a person’s risk preferences are related to the curvature of the utility of wealth function. The greater the gambler’s level of risk aversion, the more the slope of his utility function declines as wealth increases. If the gambler is risk averse, we should

|
|
|
|
|
230 |
|
DECISION UNDER RISK AND UNCERTAINTY |
observe that the rise of the utility function from $0 to $50 is larger than the rise from $50 to $100 (both intervals have a run of $50 needed to complete the standard formula for slope). More generally we can measure this decline in slope through the ratio of u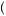 50
50 − u
− u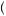 0
0 to u
to u 100
100 − u
− u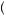 50
50 . Greater risk aversion means that u
. Greater risk aversion means that u 100
100 − u
− u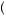 50
50 is smaller relative to u
is smaller relative to u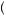 50
50 − u
− u 0
0 , implying a larger value in the right side of equation 9.16. Thus, the more risk averse the preferences, the greater the slope of the indifference curves. This is always the case when the x and y axes contain the highest and lowest value outcomes, respectively.
, implying a larger value in the right side of equation 9.16. Thus, the more risk averse the preferences, the greater the slope of the indifference curves. This is always the case when the x and y axes contain the highest and lowest value outcomes, respectively.
EXAMPLE 9.4 Allais’ Paradox
Maurice Allais was one of the earliest to criticize the expected utility model of decision under risk, believing it eliminated many of the important psychological factors involved in risky decisions. He made the argument using hypothetical choices between gambles that most readers would acknowledge seem to call expected utility theory into question. For example, suppose you had to choose between:
Gamble A: |
Gamble B: |
You receive $100 with certainty |
Probability 0.1 of receiving $500 |
|
Probability 0.89 of receiving $100 |
|
Probability 0.01 of receiving $0 |
|
|
Now suppose you were deciding between
Gamble C: |
Gamble D: |
Probability 0.11 of receiving $100 |
Probability 0.10 of receiving $500 |
Probability 0.89 of receiving $0 |
Probability 0.90 of receiving $0 |
|
|
Many choose A rather than B because of the certainty of receiving something from the gamble. However, very few would choose C over D because the 1 percent additional probability of winning something in C does not feel as if it compensates for the reduction in payoff from $500 to $100.
But these two decisions contradict the rational axioms. Note, A  B implies that
B implies that
U 100 > 0.1U 500 |
+ 0.89U 100 + 0.01U 0 |
9 17 |
|||||||||||
or |
|
|
0.1 |
|
|
|
0.01 |
|
|
||||
U 100 |
> |
U 500 |
+ |
|
U 0 . |
9 18 |
|||||||
0.11 |
0.11 |
||||||||||||
|
|
|
|
|
|
||||||||
Alternatively D C implies that |
|
|
|
|
|
|
|
|
|
|
|
|
|
0.1U 500 + 0.90U 0 > 0.11U 100 + 0.89U 0 |
9 19 |
||||||||||||
or |
|
|
|
|
|
|
|
|
|
|
|
|
|
U 100 |
|
< |
10 |
U 500 |
+ |
|
|
1 |
U 0 , |
9 20 |
|||
|
|
11 |
|||||||||||
|
|
11 |
|
|
|
|
|
||||||
|
|
|
|
Independence and Rational Decision under Risk |
|
231 |
|
which clearly contradicts equation 9.17. This is often called the Allais’ paradox or the common outcome effect.
The term common outcome effect refers to the structure of the gambles. Gambles A and C can be thought of as probability 0.11 of receiving $100 and probability 0.89 of receiving $X, where in A, X = 100 and in B, X = 0. Gambles B and D can be thought of as probability 0.1 of receiving $500, probability 0.89 of receiving $X, and probability 0.01 of receiving $0, where in B, X = 100, and in D X = 0. In all gambles, X is the common outcome (has the same value and probability in both choices). Expected utility theory implies that the value of X should not affect the gambler’s choice. However, here we have observed that people change their preference depending on whether X is 100 or 0. Economics experiments have repeatedly found evidence of the common outcome effect in risky choice.
This is a violation of the independence axiom. This is relatively easy to see in the Marschak–Machina triangle, as seen in Figure 9.3. Gambles C and D are created by sliding gambles A and B to the right by 0.89 (increasing the probability of $0 by 0.89). The line segment AB is exactly as long and of the same slope as line segment CD. Recall that under the independence axiom, indifference curves in the Marschak–Machina triangle are straight parallel lines sloping upward. Further, preferred gambles should lie to the northwest of the indifference curves. If D is preferred to C, then indifference curves must be of a slope that could place D to the northwest and C to the southeast (as pictured). However, it is impossible to find a line of identical slope that would place A to the northwest and C to the southeast. Thus, the indifference curves must change slope in different parts of the triangle, with steeper indifference curves to the west. This is a common method for finding risky choices that violate the independence axiom.
Allais’ choice problem is also an example of the certainty effect. The certainty effect is the name applied to choices in which decision makers display an irrational preference for outcomes with certainty. For example, in this case it might be that A is chosen
p(500) = 1
Probability of $500
B D
p(500) = 0 A |
|
C |
|
|
FIGURE 9.3 |
|
|
|
The Common Outcome Effect in the Marschak– |
||
|
|
||||
p(0) = 0 |
Probability of $0 |
p(0) = 1 |
Machina Triangle |
||

|
|
|
|
|
232 |
|
DECISION UNDER RISK AND UNCERTAINTY |
because of the certainty effect, even though gambles that have the same relationship in the Marschak–Machina triangle that do not involve certainty (such as C and D) would display the opposite preferences. This observation that people tend to violate the independence axiom often in preference of a certain outcome has led to the hypothesis that people do not perceive probabilities as summing to 1. Rather, they perceive a probability p of outcome X as yielding π p
p probability of receiving utility U
probability of receiving utility U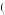 X
X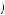 , where π
, where π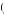 p
p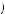 is such that π
is such that π p
p + π
+ π 1 − p
1 − p < 1, called subadditivity. Thus, uncertain outcomes are discounted relative to certain outcomes. In this framework, called probability weighting, A
< 1, called subadditivity. Thus, uncertain outcomes are discounted relative to certain outcomes. In this framework, called probability weighting, A  B implies
B implies
|
U 100 > π 0.1 U 500 + π 0.89 U 100 + π 0.01 U 0 , |
9 21 |
||||
or |
|
|
|
|
|
|
|
|
U 100 1 − π 0.89 > π 0.1 U 500 + π 0.01 U 0 |
9 22 |
|||
And D |
C implies |
|
|
|
|
|
|
π 0.1 u 500 + π 0.90 u 0 > π 0.11 u 100 + π 0.89 u 0 |
9 23 |
||||
or |
|
|
|
|
|
|
|
π 0.11 U 100 |
< π 0.1 U 500 + π 0.90 − π 0.89 U 0 . |
9 24 |
|||
Equations 9.24 |
and 9.22 |
could both hold if |
either |
π 0.11 < 1 − π 0.89 or |
||
π 0.90 |
− π 0.89 |
> π 0.01 , |
supposing the utility |
from |
$0 is positive. |
Probability |
weighting is a way to represent systematic misperception of probabilities in choice preferences. Thus, subadditivity may be one explanation for the common outcome effect.
Chris Starmer is among a group of economists who suggest regret aversion may be behind the common outcome effect. Using the case above, if the gambles were inde-
pendent, A B and regret theory imply that |
|
|
|
|
|
0.1U 100, 500 + 0.89U 100, 100 + 0.01U 100, 0 > 0, |
9 25 |
||||
or |
|
|
|
|
|
U 100, 500 + 0.1U 100, |
0 > 0, |
9 26 |
|||
and D C implies |
|
|
|
|
|
0.11 × 0.10U 100, 500 + 0.11 × 0.90U 100, 0 |
0.89 × 0.10U 0, 500 |
9 26 |
|||
+ 0.89 × 0.90U 0, 0 < 0 |
|
|
|
||
|
|
|
|
||
or |
|
|
|
|
|
U 100, 500 + 9U 100, 0 + |
89 |
U 0, 500 < 0. |
9 27 |
||
11 |
|||||
|
|
|
|
||

|
|
|
|
Independence and Rational Decision under Risk |
|
233 |
|
Equations 9.27 and 9.26 are not contradictory so long as U 0, 500
0, 500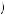 is sufficiently negative. In this case the person would feel so much regret from obtaining zero if 500 would have been drawn otherwise that their preferences reverse. Starmer and others have found some evidence that the common consequence effect and related behavior is due to the possibility of regret.
is sufficiently negative. In this case the person would feel so much regret from obtaining zero if 500 would have been drawn otherwise that their preferences reverse. Starmer and others have found some evidence that the common consequence effect and related behavior is due to the possibility of regret.
EXAMPLE 9.5 Common Ratio Effect
Allais also discovered the common ratio effect. Consider the following choices (from
Kahneman and Tversky).
Gamble A: |
Gamble B: |
You receive $3,000 with certainty |
Probability 0.80 of receiving $4,000 |
|
Probability 0.20 of receiving $0 |
|
|
Now suppose you were deciding between
Gamble C: |
Gamble D: |
Probability 0.25 of receiving $3,000 |
Probability 0.20 of receiving $4,000 |
Probability 0.75 of receiving $0 |
Probability 0.80 of receiving $0 |
|
|
Kahneman and Tversky found that about 80 percent of those asked would choose Gamble A, and about 65 percent would choose Gamble D. However, choosing A and D is a violation of expected utility. To see this, note that A  B implies
B implies
U 3000 > 0.8U 4000 |
+ 0.2U 0 |
9 28 |
and D C implies |
|
|
0.25U 3000 + 0.75U 0 < 0.2U 4000 + 0.8U 0 |
9 29 |
|
or |
|
|
U 3000 < 0.8U 4000 |
+ 0.2U 0 . |
9 30 |
Clearly, equations 9.30 and 9.28 cannot both hold. This is the common ratio effect again because of the structure of the gambles involved. Gamble C can be thought of as a 0.25 chance of playing gamble A and a 0.75 chance of receiving $0. Similarly, Gamble D can be thought of as a 0.25 chance of receiving gamble B (resulting in 0.20 probability of $4,000) and a 0.75 chance of receiving $0. Thus, the ratios of the probabilities of outcomes in gambles A and B remain the same in gambles C and D, with a common outcome added. This particular version of the common ratio effect may also be thought of as an example of the certainty effect given the involvement of Gamble A.
