
- •Brief Contents
- •Contents
- •Preface
- •Who Should Use this Book
- •Philosophy
- •A Short Word on Experiments
- •Acknowledgments
- •Rational Choice Theory and Rational Modeling
- •Rationality and Demand Curves
- •Bounded Rationality and Model Types
- •References
- •Rational Choice with Fixed and Marginal Costs
- •Fixed versus Sunk Costs
- •The Sunk Cost Fallacy
- •Theory and Reactions to Sunk Cost
- •History and Notes
- •Rational Explanations for the Sunk Cost Fallacy
- •Transaction Utility and Flat-Rate Bias
- •Procedural Explanations for Flat-Rate Bias
- •Rational Explanations for Flat-Rate Bias
- •History and Notes
- •Theory and Reference-Dependent Preferences
- •Rational Choice with Income from Varying Sources
- •The Theory of Mental Accounting
- •Budgeting and Consumption Bundles
- •Accounts, Integrating, or Segregating
- •Payment Decoupling, Prepurchase, and Credit Card Purchases
- •Investments and Opening and Closing Accounts
- •Reference Points and Indifference Curves
- •Rational Choice, Temptation and Gifts versus Cash
- •Budgets, Accounts, Temptation, and Gifts
- •Rational Choice over Time
- •References
- •Rational Choice and Default Options
- •Rational Explanations of the Status Quo Bias
- •History and Notes
- •Reference Points, Indifference Curves, and the Consumer Problem
- •An Evolutionary Explanation for Loss Aversion
- •Rational Choice and Getting and Giving Up Goods
- •Loss Aversion and the Endowment Effect
- •Rational Explanations for the Endowment Effect
- •History and Notes
- •Thought Questions
- •Rational Bidding in Auctions
- •Procedural Explanations for Overbidding
- •Levels of Rationality
- •Bidding Heuristics and Transparency
- •Rational Bidding under Dutch and First-Price Auctions
- •History and Notes
- •Rational Prices in English, Dutch, and First-Price Auctions
- •Auction with Uncertainty
- •Rational Bidding under Uncertainty
- •History and Notes
- •References
- •Multiple Rational Choice with Certainty and Uncertainty
- •The Portfolio Problem
- •Narrow versus Broad Bracketing
- •Bracketing the Portfolio Problem
- •More than the Sum of Its Parts
- •The Utility Function and Risk Aversion
- •Bracketing and Variety
- •Rational Bracketing for Variety
- •Changing Preferences, Adding Up, and Choice Bracketing
- •Addiction and Melioration
- •Narrow Bracketing and Motivation
- •Behavioral Bracketing
- •History and Notes
- •Rational Explanations for Bracketing Behavior
- •Statistical Inference and Information
- •Calibration Exercises
- •Representativeness
- •Conjunction Bias
- •The Law of Small Numbers
- •Conservatism versus Representativeness
- •Availability Heuristic
- •Bias, Bigotry, and Availability
- •History and Notes
- •References
- •Rational Information Search
- •Risk Aversion and Production
- •Self-Serving Bias
- •Is Bad Information Bad?
- •History and Notes
- •Thought Questions
- •Rational Decision under Risk
- •Independence and Rational Decision under Risk
- •Allowing Violations of Independence
- •The Shape of Indifference Curves
- •Evidence on the Shape of Probability Weights
- •Probability Weights without Preferences for the Inferior
- •History and Notes
- •Thought Questions
- •Risk Aversion, Risk Loving, and Loss Aversion
- •Prospect Theory
- •Prospect Theory and Indifference Curves
- •Does Prospect Theory Solve the Whole Problem?
- •Prospect Theory and Risk Aversion in Small Gambles
- •History and Notes
- •References
- •The Standard Models of Intertemporal Choice
- •Making Decisions for Our Future Self
- •Projection Bias and Addiction
- •The Role of Emotions and Visceral Factors in Choice
- •Modeling the Hot–Cold Empathy Gap
- •Hindsight Bias and the Curse of Knowledge
- •History and Notes
- •Thought Questions
- •The Fully Additive Model
- •Discounting in Continuous Time
- •Why Would Discounting Be Stable?
- •Naïve Hyperbolic Discounting
- •Naïve Quasi-Hyperbolic Discounting
- •The Common Difference Effect
- •The Absolute Magnitude Effect
- •History and Notes
- •References
- •Rationality and the Possibility of Committing
- •Commitment under Time Inconsistency
- •Choosing When to Do It
- •Of Sophisticates and Naïfs
- •Uncommitting
- •History and Notes
- •Thought Questions
- •Rationality and Altruism
- •Public Goods Provision and Altruistic Behavior
- •History and Notes
- •Thought Questions
- •Inequity Aversion
- •Holding Firms Accountable in a Competitive Marketplace
- •Fairness
- •Kindness Functions
- •Psychological Games
- •History and Notes
- •References
- •Of Trust and Trustworthiness
- •Trust in the Marketplace
- •Trust and Distrust
- •Reciprocity
- •History and Notes
- •References
- •Glossary
- •Index
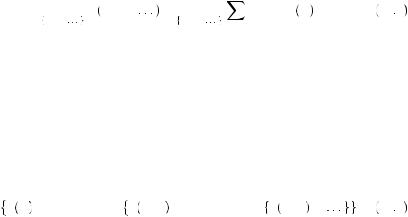
|
|
|
|
|
348 |
|
COMMITTING AND UNCOMMITTING |
Odysseus further commands his men to tie him to the mast so that he cannot escape. While thus tied to the mast, he could be exposed to the temptation but would not have the choice to steer the ship toward the Sirens’ song. He could thus become the only man to have heard their song and lived. By restricting his choice set, he could indulge in the song without giving in to the temptation that accompanied it. In this case, he could consider himself better off for making the commitment because he expected to do something that would harm him if he was not thus committed. In other words, Odysseus must have believed he would make the wrong choice in order for being tied to the mast to make sense. In a similar sense, commitment mechanisms can be used by those who recognize their own time inconsistency to tie themselves to the mast.
Rationality and the Possibility of Committing
The fully additive exponential model of discounting predicts that people will display time-consistent preferences. In this case, people would have no desire to precommit to a specific path because they know they would eventually take that preferred path anyway. There is no temptation to do anything else in the rational model. Consider again the fully additive model presented in Chapter 12, in which the decision maker solves
max U c1, c2, |
= max |
T |
δi − 1u ci |
13 1 |
|
i = 1 |
|||||
c1,c2, |
c1, c2, |
|
|
||
|
|
|
subject to whatever budget constraint he faces. This model assumes that consumers determine their entire consumption path, the consumption quantity for each individual time period, all at the initial time period. Thus, this model in reality assumes that the consumer can commit to the consumption path that solves equation 13.1. If instead we are attempting to model the case in which consumers cannot commit to a consumption path, then the model must reflect that consumers decide on the level of consumption in this period based upon what they believe they will decide to do in the future. Thus, in period t, the consumer solves the recursive optimization problem:
maxct <wt u ct + δ maxct + 1<wt + 1 u ct + 1 + δ2 maxct + 2<wt + 2 u ct + 2 + |
, 13 2 |
where wt is the budget constraint in period t that depends on consumption in all prior periods.
Equation 13.2 can be a little difficult to interpret at first. Consumers maximize their utility of consumption in this period given that they will behave so as to maximize their utility of consumption again in each future period as well. This may be easiest to see in a finite horizon problem. Consider consumers who have initial wealth w and must allocate it to consumption over three periods. After the third period, they will die, and no further consumption will be possible. Further suppose that the cost of one unit of consumption is one unit of wealth. Then, when consumers are deciding on consumption in the first period, they anticipate the maximization problem they will face in the second and third periods.

|
|
|
|
Rationality and the Possibility of Committing |
|
349 |
|
A fully continuous problem for the general consumption case is presented in the Advanced Concept box at the end of the chapter. For a simple example, consider the discrete-choice problem where, in the first and the second period, laborers can either decide to work, receiving instantaneous utility of w, or shirk, receiving instantaneous utility of s, where s > w. In the third period, the laborers receive $10 for each day they worked, yielding instantaneous utility u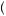 10x
10x = 10x, where x is the number of days worked. In the third period, the laborers have no actions they can take, and thus they simply receive instantaneous utility of the payment. If we consider the choice the laborers face in the second period, given their action in the first period, they must solve
= 10x, where x is the number of days worked. In the third period, the laborers have no actions they can take, and thus they simply receive instantaneous utility of the payment. If we consider the choice the laborers face in the second period, given their action in the first period, they must solve
maxz2 = w,s z2 + δ × 10x, |
13 3 |
where zi is the action chosen in period i, and
2 |
if |
z1 = w, z2 = w |
|
x = 1 |
if |
z1 = w, z2 = s . |
13 4 |
1 |
if |
z1 = s, z2 = w |
|
0 |
if |
z1 = s, z2 = s |
|
They will choose to work so long as
w + δ x1 + 10 > s + δx1, |
13 5 |
where x1 is the reward resulting from the action chosen in the first period. This can be rewritten as
10δ > s − w. |
13 6 |
Let us suppose that this is the case, so that no matter what was chosen in the first period, laborers will choose to work in the second period. Then, in the first period, laborers face the problem
maxz1 = w,s
w,s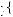 z1 + δ maxz2 =
z1 + δ maxz2 = w,s
w,s
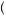 z2 + δ × 10x
z2 + δ × 10x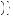 = maxz1 =
= maxz1 = w,s
w,s z1 + δw + δ2
z1 + δw + δ2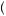 x1 + 10
x1 + 10 ,
, 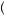 13
13 7
7
where the second and third terms result from the laborer choosing to work in the second period regardless of the first-period decision. The laborer will decide to work in the first period if
w + δw + δ220 > s + δw + δ210 |
13 8 |
or, rewriting, |
|
10δ2 > s − w. |
13 9 |

|
|
|
|
|
350 |
|
COMMITTING AND UNCOMMITTING |
Let us suppose that this is not the case, but that the laborer decides to shirk because 10δ2, the discounted reward for working in the first period, is less than the immediate difference in utility between working and shirking, s − w. For example, suppose s = 3, w = − 2, δ = 0.7. Then, from equation 13.6, 10δ = 7, which is greater than s − w = 5, implying the laborer will decide to work in the second period. However, 10δ2 = 4.9, which is less than s − w = 5. Thus, according to equation 13.9, the laborer would choose to shirk in the first period. Thus, the recursive optimization problem results in the laborer choosing to shirk in the first period, working in the second period and receiving $10 in pay in the third period.
This method of solving for the optimal sequence of decisions is called backward induction, and it is commonly used by economists to model decision makers’ anticipation of behavior (either their own or others’) in future periods. This model essentially assumes that the laborer will optimize in each period, conditional on assuming he will reoptimize in each subsequent period. Backward induction is most often used by economists to model games involving sequential decisions by multiple players. In the case of a potentially time-inconsistent decision maker, it may be thought of as a game involving decisions by several different selves, one for each period of the optimization. Backward induction yields the optimal plan, taking account of the potential for timeinconsistent preferences. In the case of exponential discounting, however, the decision maker should not display time-inconsistent preferences.
To see this last point, consider the standard fully additive model from equation 13.1. In the framework of our laborer, in the first period he would simply solve
maxz1,z2 w,s z1 + δz2 + δ210x. |
13 10 |
In this problem there are several possibilities, and the utility of all possible choices can be written as
|
w + δw + δ220 |
if z1 = w, z2 = w |
|
|
U z1, z2 = |
w + δs + δ210 |
if |
z1 = w, z2 = s |
|
s + δw + δ210 |
if |
z1 = s, z2 = w . |
13 11 |
|
|
s + δs |
if |
z1 = s, z2 = s |
|
Note from equation 13.11 that the possible choices 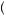 z1 = w, z2 = w
z1 = w, z2 = w and
and  z1 = s, z2 = w
z1 = s, z2 = w are identical to the choices from the recursive problem in equation 13.7. Among these two options, the laborer would again choose
are identical to the choices from the recursive problem in equation 13.7. Among these two options, the laborer would again choose  z1 = s, z2 = w
z1 = s, z2 = w , indicating no time-inconsistent preferences. If there is any chance for time-inconsistent preferences, it must come from one of the other options. But each of the other options is clearly dominated by one of the two choices from equation 13.7. Choosing
, indicating no time-inconsistent preferences. If there is any chance for time-inconsistent preferences, it must come from one of the other options. But each of the other options is clearly dominated by one of the two choices from equation 13.7. Choosing 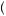 z1 = s, z2 = s
z1 = s, z2 = s could only happen if
could only happen if
s + δs > s + δw + δ210, |
13 12 |
the utility resulting from 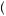 z1 = s, z2 = w
z1 = s, z2 = w , which implies that 10δ < s − w. But this contradicts our assumption from equation 13.6. Choosing
, which implies that 10δ < s − w. But this contradicts our assumption from equation 13.6. Choosing 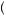 z1 = w, z2 = w
z1 = w, z2 = w could only occur if
could only occur if

|
|
|
|
|
Commitment under Time Inconsistency |
|
351 |
|
|
w + δw + δ220 > s + δw + δ210, |
13 13 |
|
|
|
the utility resulting from z1 = s, z2 = w , which implies that δ210 > s − w. But we also |
|
|
||
already assumed that this was not the case. Thus, there is no possibility for time- |
|
|
||
inconsistent preferences. |
|
|
|
|
In general, with exponential discounting, the decision problem of the decision maker |
|
|
||
in the nth period from the point of view of the decision maker in the nth period always |
|
|
||
has the same solution as the optimization problem from the point of view of the first |
|
|
||
period given the first n − 1 choices. Backward induction can only eliminate choices that |
|
|
||
would be dominated from the point of view of a first-period decision maker. This is |
|
|
||
because every period after the nth period is discounted by δ relative to the nth period, |
|
|
||
just as it would be from the point of view of the first period. The property of stationarity |
|
|
||
guarantees that backward induction never results in a conflict with the standard opti- |
|
|
||
mization. Stationarity tells us that exponential discounting results in preferences that |
|
|
||
remain the same when trading off consumption in period t and t + |
, no matter the value |
|
|
|
of t. Thus, the fact that the second period is one period removed from the third drives the |
|
|
||
decision to work in period 2 regardless of how far distant period 2 may be from |
|
|
||
the decision maker’s point of view. |
|
|
|
|
Thus, in the case of exponential discounting, decision makers need not worry about |
|
|
||
enforcing their current will on their future self. Decision makers do not display time- |
|
|
||
inconsistent preferences; their preferences today about future consumption will be |
|
|
||
realized whether they can commit to a consumption path today (as in equation 13.1) or |
|
|
||
can only commit to today’s level of consumption (as in the recursive optimization |
|
|
||
problem in equation 13.2). Choosing the consumption path implied by the recursive |
|
|
||
optimization problem implies exactly the same level of utility as committing to |
|
|
||
the consumption path that solves the standard optimization problem. Committing to a |
|
|
||
consumption path now would yield the utility stream described by |
z1 = s, z2 = w . Not |
|
|
|
committing would also yield the utility stream described by 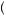 z1 = s, z2 = w
z1 = s, z2 = w . In fact these are identical, and thus decision makers should not be willing to give up anything to obtain a commitment mechanism.
. In fact these are identical, and thus decision makers should not be willing to give up anything to obtain a commitment mechanism.
Commitment under Time Inconsistency
Now consider a sophisticated person who faces the same three-period consumption problem but who discounts the utility of future consumption according to the quasihyperbolic discounting model. If a decision maker could commit to a consumption path now, he would choose
max u c1 + |
T |
βδi − 2u ci |
13 14 |
i = 2 |
|||
c1,c2, |
|
|
|
subject to whatever budget constraint might apply. Thus, decision makers would choose the consumption path that maximizes their current perception of utility and impose this consumption stream on future (potentially unwilling) versions of themselves.

|
|
|
|
|
352 |
|
COMMITTING AND UNCOMMITTING |
People without access to a credible way to commit to future acts must then anticipate their future actions by solving the recursive optimization problem. Only now, because of the quasi-hyperbolic discount function, the problem becomes somewhat more complicated than that written in equation 13.2. Instead, the decision maker must solve
maxc1 u c1 + |
T |
βδi − 2u ci* , |
13 15 |
i = 2 |
where c*i is defined recursively as solving
maxc |
u ci + |
T |
βδ j − 2u |
c* |
, |
13 16 |
|
j = i + 1 |
|||||||
i |
|
|
j |
|
|
where the budget set in each period is conditioned on the consumption decisions from previous periods. We refer to decision makers who behave as if they solve the recursive optimization problem as sophisticated, and we refer to those who solve the standard maximization problem (as in equation 13.1) as naïve or committed, depending on the context. Sophisticated decision makers anticipate their future behavior, and naïve decision makers do not consider how their future plans will change based upon changes in how they discount a particular period relative to other periods. Alternatively, those who can commit to a particular consumption path will also solve equation 13.1 because they need not worry about their future behavior. The commitment mechanism ensures that behavior conforms to their current preferences.
To develop some intuition about what this model means, consider the three-period model from the previous section, only now suppose that the laborer discounts according to the quasi-hyperbolic model, with parameters β and δ. We can solve this problem by backward induction as before. In the third period, laborers face no choices but just receive the reward for their prior actions. Thus we begin by considering the choice from the point of view of second-period laborers. In this case, laborers will solve
maxz2 = w,s z2 + β × 10x. |
13 17 |
They will choose to shirk so long as
w + β x1 + 10 < s + βx1, |
13 18 |
where x1 is the reward resulting from the action chosen in the first period. This can be rewritten as
10β < s − w. |
13 19 |
Let us suppose that this is the case. Then the laborer chooses to shirk in the second period no matter what happens in the first period. Then, in the first period, the laborer would solve
maxz1 = w,s
w,s z1 + β maxz2 =
z1 + β maxz2 = w,s
w,s z2 + δ × 10x
z2 + δ × 10x = maxz1 =
= maxz1 = w,s
w,s z1 + βs + βδx1,
z1 + βs + βδx1,  13
13 20
20

|
|
|
|
Commitment under Time Inconsistency |
|
353 |
|
where the second and third terms result from the laborer choosing to shirk in the second period regardless of the first-period decision. The laborer will decide to work in the first period if
w + βs + βδ10 > s + βs |
13 21 |
or, rewriting, |
|
10βδ > s − w. |
13 22 |
But if equation 13.19 holds, clearly equation 13.22 cannot. Thus, the laborer would choose to shirk in both periods and earn no reward.
We can contrast this solution with the choice made if the laborer could commit to his work plan in the second period without the possibility of changing his mind. Then, the laborer in the first period would solve
maxz1,z2 w,s z1 + βz2 + βδ10x. |
13 23 |
Proceeding as in the previous section, this is equivalent to maximizing the function
|
w + βw + βδ20 |
if z1 = w, z2 = w |
|
|
U z1, z2 = |
w + βs + βδ10 |
if |
z1 = w, z2 = s |
|
s + βw + βδ10 |
if |
z1 = s, z2 = w . |
13 24 |
|
|
s + βs |
if |
z1 = s, z2 = s |
|
In this case, the choices 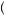 z1 = w, z2 = s
z1 = w, z2 = s and
and 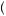 z1 = s, z2 = s
z1 = s, z2 = s are identical to the choices that were available to the first-period decision maker using backward induction in
are identical to the choices that were available to the first-period decision maker using backward induction in
equation 13.20, and thus clearly 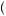 z1 = s, z2 = s
z1 = s, z2 = s would dominate between these two
would dominate between these two
options. But the other two options were not available. The option |
z1 = w, z2 = w would |
||
be chosen if w + βw + βδ20 > s + βs, or, rewriting, |
|
||
|
βδ |
|
|
20 × |
|
> s − w. |
13 25 |
1 + β |
|||
Given that equation 13.22 holds, this could only be the case if 2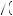 1 + β
1 + β is much greater than 1.
is much greater than 1.
Let us suppose that this is not the case. For example, suppose s = 3, w = − 2, δ = 0.7, β = 0.5. Then,
20 × |
βδ |
4.67 < s − w = 5, |
13 26 |
1 + β |
implying that the laborer would prefer to shirk in both periods than to work in both periods. The remaining choice,  z1 = s, z2 = w
z1 = s, z2 = w , would be chosen over the other options
, would be chosen over the other options

|
|
|
|
|
|
354 |
|
COMMITTING AND UNCOMMITTING |
|
|
|
if s + βw + βδ10 > s + βs, or, rewriting, if δ10 > s − w. Using the numerical example, this |
||
|
|
would hold because δ10 = 7 > s − w = 5. Thus, given the option to bind himself to a work |
||
|
|
plan in the future, the laborer will choose to shirk today and work tomorrow. Of course, |
||
|
|
he will not really want to work when tomorrow comes, but his commitment eliminates |
||
|
|
the choice. He is a slave to his prior preferences. |
|
|
|
|
|
We have examined a simple example with only four possible decision paths. A |
|
|
|
more general example of the exponential, quasi-hyperbolic discounting, naïve, |
||
|
|
committed, and sophisticated decision makers is presented in the Advanced Concept |
||
|
|
box at the end of the chapter, though the discussion requires substantial use of |
||
|
|
calculus. In general, the decision path for the recursive optimization problem always |
||
|
|
lies between the planned consumption path of the naïve quasi-hyperbolic discounter |
||
|
|
(which is identical to the optimal consumption path for a committed decision maker) |
||
|
|
and the consumption path of the rational exponential discounter with discount |
||
|
|
factor of δ. |
|
|
|
|
|
Without the ability to commit, the decision maker will choose to shirk in the first |
|
|
|
period, just as the naïve quasi-hyperbolic discounter would. However, naïve discounters |
||
|
|
do this thinking they will be able to make up for their shirking in the next period. |
||
|
|
Committed decision makers could force themselves to work in the next period and |
||
|
|
potentially obtain a higher level of utility. The lack of ability to commit leads to a loss in |
||
|
|
utility to decision makers. Using the numerical example, the utility of the committed |
||
|
|
decision maker is |
|
|
|
|
|
Ucommitted = s + βw + βδ10 = 5.5. |
13 27 |
|
|
Instead, the sophisticated, but uncommitted decision maker will obtain |
|
|
|
|
|
Usophisticated = s + βs = 4.5. |
13 28 |
|
|
Sophisticated decision makers obtain a lower utility knowing that they cannot count on |
||
|
|
their second-period self to save them. It is always the case that the sophisticated decision |
||
|
|
maker will be made no worse off, but could be made better off, by the option of |
||
|
|
committing. |
|
|
|
|
|
Finally, consider the naïve decision maker explored in Chapter 12. People who are |
|
naïve regarding their time inconsistency will solve equation 13.23 to determine this period’s work plan. But, if they are not committed to their work plan, they will reoptimize every period and execute a different plan in the future. In this particular case, naïve decision makers will reoptimize in period 2 and determine to shirk again, obtaining the same utility as the sophisticate. In general, a naïve decision maker’s utility (evaluated from the point of view of the first-period decision maker) will be as low as, or lower than, the sophisticate’s. Naïve decision makers would not be willing to pay for a commitment device because they don’t foresee that they will deviate from their planned consumption path. Thus, they are worse off for their inability to predict their own behavior in the future. In each case, this would lead to indulgence and greater consumption (or shirking) in early periods, leaving little for consumption in later periods.

|
|
|
|
|
|
|
|
|
|
|
|
Commitment under Time Inconsistency |
|
355 |
|
|
EXAMPLE 13.1 Savings Clubs and Federal Tax Refunds |
|
|
||||
|
|
|
|||||
|
|
|
|
|
|||
Though they are not particularly popular anymore, at one time many people belonged to |
|
|
|||||
a Christmas club. To join a Christmas club, you would stop by your bank and sign an |
|
|
|||||
agreement that would commit you to transferring a certain amount of money out of your |
|
|
|||||
checking account every week to place it in an account that could only be accessed in |
|
|
|||||
December as Christmas approached. The idea was to allow bank patrons to save up for |
|
|
|||||
their Christmas shopping without having to remember or to make the decision each |
|
|
|||||
month to put some aside. The person was committed to save for Christmas, and the bank |
|
|
|||||
would pay the customer lower interest than would accrue in a regular savings account in |
|
|
|||||
return. The idea caught fire during the Great Depression, as more families had difficulty |
|
|
|||||
providing for a traditional Christmas. So why would families give up the added interest to |
|
|
|||||
commit to something they could very easily accomplish without the commitment? |
|
|
|||||
|
Christmas clubs are mostly a thing of the past, but many people persist in using |
|
|
||||
federal income tax withholding as a form of saving. More than three fourths of those |
|
|
|||||
filing a federal income tax form receive some income tax refund, with the average refund |
|
|
|||||
totaling about $3,000. Each paycheck, the government withholds a certain amount from |
|
|
|||||
each wage-earner’s pay to cover anticipated income tax. The amount withheld is based |
|
|
|||||
upon how much the worker earns and on the number of exemptions he claims. If, on |
|
|
|||||
average, workers are receiving a substantial refund, they could simply claim a greater |
|
|
|||||
number of exemptions and reduce the withholding. Instead, many intentionally have |
|
|
|||||
excess amounts withheld, worried that they would not be able to save the amount if they |
|
|
|||||
were left to their own willpower. The federal withholding creates a commitment device |
|
|
|||||
that allows them to save for a new TV or other products. However, the federal govern- |
|
|
|||||
ment does not pay interest on these excess withholdings. Thus, people who receive |
|
|
|||||
refunds are forgoing all interest on the money they have saved over that year. |
|
|
|||||
|
In modeling committed saving, let us suppose that Guadalupe earns $30 each week. |
|
|
||||
On the first of the year, Guadalupe has 48 weeks to save before the money becomes |
|
|
|||||
available. Suppose that he is a quasi-hyperbolic discounter, with β = 0.5 and δ = 0.97. |
|
|
|||||
Moreover, suppose that he has an instantaneous utility of consumption (for a week of |
|
|
|||||
consumption) given by u c |
= |
c, but that in week 49, Guadalupe has utility given by |
|
|
|||
u49 c49, χ = 0.371 × χc49, |
where χ is the |
amount spent on Christmas gifts. Let us |
|
|
|||
suppose that there is no other reason to save, and so there is no additional utility of |
|
|
|||||
saving in week 49. Finally, suppose that the regular savings account offers an annual |
|
|
|||||
interest rate of 5 percent, compounded weekly. Thus, if Guadalupe has s in his savings |
|
|
|||||
account at week t, he earns |
0.05 ÷ 52 × s |
0.001s in interest. In each period, savers |
|
|
|||
can choose to spend any savings, and |
thus their budget constraint is given by |
|
|
||||
30 + 1.001 st − 1, where st − 1 is the savings from last period. Initial savings is equal to 0. |
|
|
|||||
|
Further, let us suppose that Guadalupe is sophisticated, and thus anticipates his |
|
|
||||
savings behavior in the future. We can solve this problem using backward induction. In the 49th week, Guadalupe will have savings s49, and thus will solve
maxc49,χ 0.371 × χc49 |
13 29 |

|
|
|
|
|
356 |
|
COMMITTING AND UNCOMMITTING |
subject to the constraint χ + c49 ≤ 1.001s48 + 30. Because marginal utility is always positive, Guadalupe will continue to consume in each period until the budget constraint is met with equality:
χ + c49 = 1.001s48 + 30. |
13 30 |
This problem is identical to the single-period consumption problem with two possible goods presented in the early chapters of this book. Thus, the solution can be found where the marginal utility of c49 and χ are equal (noting that both have the same price, p = 1). The marginal utility of c49 implied by equation 13.29 is
uc49 c49, χ = 0.371 × 0.5χ2c49 |
13 31 |
and the marginal utility with respect to χ is
uχ |
c49 |
, χ = 0.371 × 0.5χc2 . |
13 32 |
|
|
49 |
|
Setting equation 13.31 equal to equation 13.32 implies that
χ = c49 |
13 33 |
Substituting equation 13.33 into the budget constraint for period 49, equation 13.30, yields
c49* = |
|
1.001s48 + 30 |
= 0.5005s48 + 15 |
13 34 |
|
2 |
|
||||
|
|
|
|
||
χ* = |
1.001s48 + 30 |
= 0.5005s48 + 15. |
13 35 |
||
2 |
|
||||
|
|
|
|
||
Given this solution to the last week, we can solve the 48th week’s problem, which is now given by
max |
c48 |
,s48 |
V c , s |
48 |
= |
c |
+ β |
0.371 c* |
χ* |
|
48 |
|
48 |
|
49 |
13 36 |
|||
|
|
|
|
|
|
|
+ β |
|
|
|
|
|
|
|
= |
c48 |
0.371 0.5005s48 + 15 |
||
subject to the constraint c48 + s48 ≤ 1.001s47 + 30. Again, the budget constraint must hold with equality
c48 + s48 = 1.001s47 + 30. |
13 37 |
This problem is now identical to a single-period consumption problem with two goods: c48 and s48. The solution is given where the marginal utility of each good is equal. The marginal utility of consumption, c48 is given by

|
|
|
|
|
|
|
|
|
|
Commitment under Time Inconsistency |
|
357 |
|
||||
Vc48 c48, s48 |
= |
1 |
c |
− 21 |
13 38 |
|
|
|
2 |
|
|
||||||
|
|
|
48 |
|
|
|
|
|
and the marginal utility with respect to savings, s48, is given by
Vs48 c48, s48 = β × 0.371 × 0.5005 0.1857β. |
13 39 |
Setting equation 13.38 equal to equation 13.39 yields
c48* |
1 |
29. |
13 40 |
|
0.1379β2 |
||||
|
|
|
Substituting equation 13.40 into the budget constraint 13.37 yields
s48* 1.001s47 + 1. |
13 41 |
Note that because income is $30, we are assured that c48* is feasible. We can then solve the problem for week 47 as a function of s46 using similar methods, and so on until we reach week 1.
Following the same procedure to solve for consumption and savings in week 47 obtains
maxc47,s47 V  c48, s48
c48, s48 =
=  c47 + β
c47 + β  c48 + δ
c48 + δ 0.371
0.371 0.5005s48 + 15
0.5005s48 + 15
=  c47 + β
c47 + β  29 + δ
29 + δ 0.371
0.371 0.5005
0.5005 1.001s47 + 1
1.001s47 + 1 + 15
+ 15

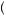 13
13 42
42
subject to the budget constraint c47 + s47 ≤ 1.001s46 + 30, which will again hold with equality. The marginal utility of consumption, c47, is now given by
Vc47 c47, s47 |
= |
1 |
c |
− 21 |
13 43 |
|
2 |
||||||
|
|
|
47 |
|
and the marginal utility of savings, s47, is now given by
Vs47 c47, s47 = βδ0.371 × 0.5005 × 1.001 0.09. |
13 44 |
Setting the marginal utilities equal yields
c47 = 30.76. |
13 45 |
But note that this is only feasible if Guadalupe has saved enough from prior periods to produce $0.76 in addition to the $30 in income earned for the period. Otherwise, he will simply decide to consume the entire budget, c49 = 1.001s46 + 30. Thus, we obtain c47 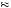 min
min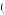 1.001s46 + 30, 30.76
1.001s46 + 30, 30.76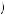 . In fact, in all weeks 47 and before, we obtain a solution such that Guadalupe will consume all budget up to some constant kt , where in period 47 k47 = 30.76. Thus in any week 47 and before with kt > 1.001st − 1 + 30, Guadalupe will decide to consume all of his wealth. If we solve all of the periods using backward induction until week 1, we find that k1 > 30. Moreover, each period’s constant kt until
. In fact, in all weeks 47 and before, we obtain a solution such that Guadalupe will consume all budget up to some constant kt , where in period 47 k47 = 30.76. Thus in any week 47 and before with kt > 1.001st − 1 + 30, Guadalupe will decide to consume all of his wealth. If we solve all of the periods using backward induction until week 1, we find that k1 > 30. Moreover, each period’s constant kt until

|
|
|
|
|
358 |
|
COMMITTING AND UNCOMMITTING |
week 47 exceeds the implied budget constraint. Thus, sophisticates consume all of their income each week until the week before Christmas, in which they will decide to save $1. Then the next week they cut their consumption in half in order to spend half of their income (and half of the $1 in savings) on Christmas presents. This results in overall utility (evaluated in week 1) of U = c1 + β
c1 + β  δi − 2
δi − 2 ci + 0.371 × βδ47
ci + 0.371 × βδ47 χc49
χc49  82.
82.
Now suppose Guadalupe is faced with the choice of making a binding commitment to take the same amount each week and put it in a savings account that would earn interest rate r 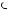
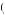 0, 1
0, 1 until December. For simplicity, suppose that if you choose to participate in this Christmas club, you cannot participate in the standard savings account, so that all income not placed in the Christmas account will be consumed each period. Moreover, suppose that all savings will begin in period 2. Now Guadalupe solves
until December. For simplicity, suppose that if you choose to participate in this Christmas club, you cannot participate in the standard savings account, so that all income not placed in the Christmas account will be consumed each period. Moreover, suppose that all savings will begin in period 2. Now Guadalupe solves
maxs 30 + β |
48 |
δi − 2 30 − s + 0.371 × βδ47 χc49 |
13 46 |
i = 2 |
where
χ + c49 |
≤ 30 + |
48 |
|
i = 2 |
|||
|
|
s 1 + |
r |
49 − i |
|
|
, |
13 47 |
|||
52 |
||||
|
|
|
the budget constraint that results from saving s each period at annual interest rate r, compounded weekly. This constraint will hold with equality.
Just as before, Guadalupe decides to divide all wealth in the last period evenly between Christmas presents and consumption to find the level of consumption and spending that equates marginal utility across the two activities. Thus, the budget constraint equation 13.47 implies that
30 + |
48 |
s 1 + |
r |
49 − i |
30 + |
48 |
s 1 + |
|
r |
49 − i |
|
|
|
i = 2 |
52 |
i = 2 |
52 |
|
|
||||||||
χ × c49 = |
|
|
|
× |
|
|
. |
13 48 |
|||||
|
|
|
|
|
|
|
|
|
|
||||
|
|
2 |
|
|
|
2 |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
||
Thus, by substituting equation 13.48 into equation 13.46 the problem can be rewritten as
maxsV s = 30 + 30 − sβ |
48 |
δi − 2 + 0.371 |
|
|||
|
i = |
2 |
|
|
13 49 |
|
× βδ47 30 + s |
48 |
1 + |
r |
49 − i |
||
. |
||||||
|
|
|
||||
i = 2 |
52 |
|
||||
This is similar to the problem of utility maximization in one good, in this case s. The solution occurs where the marginal utility of s is equal to zero. Saving less than this results in positive marginal utility of savings, meaning Guadalupe could increase his utility simply by increasing savings. Above this point, Guadalupe has negative marginal utility from savings, meaning he could increase utility simply by decreasing savings. This solution is depicted in Figure 13.1, where the top panel displays the discounted utility function V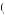 s
s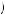 , the bottom panel displays the corresponding marginal utility function VS
, the bottom panel displays the corresponding marginal utility function VS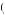 s
s , and the horizontal axis measures per-period savings.
, and the horizontal axis measures per-period savings.
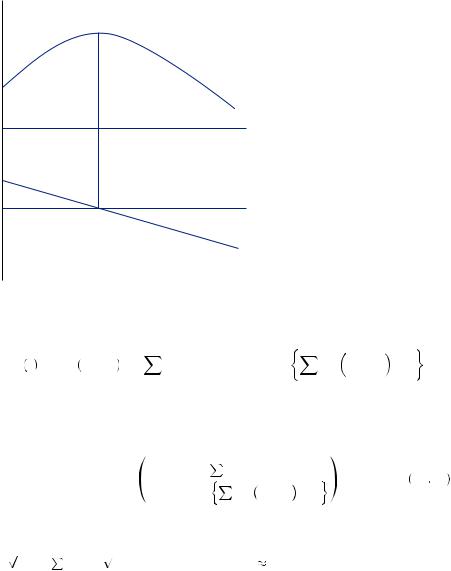
|
|
|
|
Commitment under Time Inconsistency |
|
359 |
|
V
V (s)
S
VS
0
VS (s) FIGURE 13.1
Optimal Savings with a Christmas Club
The marginal utility of s in this case can be written as
Vs s = − |
1 |
30 − s |
− 21 |
β |
48 |
δ |
i − 2 |
+ 0.371 |
× βδ |
47 |
48 |
2 |
|
i = 2 |
|
|
i = 2 |
1 + |
r |
49 |
. |
|
|
− i |
|
|
52 |
|
|
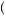 13
13 50
50
Setting equation 13.59 equal to zero yields the solution
|
|
48 |
δi − 2 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|||
s = 30 − |
|
i = 2 |
|
|
|
|
|
. |
13 51 |
0.742 × δ47 |
48 |
|
1 + |
|
r |
49 − i |
|||
|
|
|
|
|
|||||
|
i = |
1 |
52 |
|
|
|
|||
|
|
|
|
|
|
||||
If r = 0, so Guadalupe earns no interest, s = 21.11, and he thus commits to save almost
two |
thirds |
of his income |
in every period after |
the |
first. This |
leads to |
utility of |
|
U = |
30 + β |
48 |
δi − 2 8.89 |
+ 0.371 × βδ471015.41 |
87, |
which is |
greater |
than that |
i = 2 |
||||||||
obtained from not enrolling in the Christmas club and following the uncommitted strategy discussed earlier when interest is available. Thus Guadalupe would give up all interest in order to force himself to save up for Christmas.
Instead, suppose we solved for the r that would make Guadalupe indifferent between committing to the Christmas club and not. The interest rate that leads to indifference is around r  − 0.3, leading to a savings per week of s
− 0.3, leading to a savings per week of s  18 and ultimate utility of U
18 and ultimate utility of U 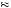 82. In other words, people who display quasi-hyperbolic discounting according to the parameters we have specified and who are sophisticated enough to recognize the time inconsistency in their behavior would be willing to give up about a third of their savings every year just to have the commitment device that ensures that
82. In other words, people who display quasi-hyperbolic discounting according to the parameters we have specified and who are sophisticated enough to recognize the time inconsistency in their behavior would be willing to give up about a third of their savings every year just to have the commitment device that ensures that

|
|
|
|
|
360 |
|
COMMITTING AND UNCOMMITTING |
they will save. Although this is an extreme example, it illustrates how knowing that you will procrastinate in the future as well as in the present does not eliminate the welfare loss from time inconsistency. Recognizing the time inconsistency can increase your immediate well-being if commitment mechanisms are available, but there may be a heavy cost to pay for such a device.
Commitment devices have also proved to be an effective means to spur savings for retirement. Richard Thaler and Shlomo Benartzi demonstrated this when such a plan was offered to the employees of a particular manufacturing firm. Given the opportunity to commit themselves to put a fraction of future pay raises into a retirement investment, 78 percent opted to join the program, with the overwhelming majority continuing in the program through several subsequent pay raises. The retirement savings rate among participants increased from an average of 3.5 percent to 13.6 percent.
EXAMPLE 13.2 Homework Due Dates
If people recognize that they have a problem with procrastination, one result is that they may be willing to set binding deadlines for themselves. This is a form of commitment mechanism. In fact, Dan Ariely and Klaus Wertenbroch used a class of M.B.A. students to explore this possibility.
Of the students in their class, 51 were assigned three papers and told that they could be turned in at any time during the semester. The students were given the option to set whatever deadlines they wished for each of the papers. The papers would be graded such that students would lose 1 percent of their grade for every day after the deadline in which the paper had not yet been turned in. There would be no penalty for setting the deadlines later rather than earlier. In this case, time-consistent decision makers would simply decide to set the deadline at the last day of class for all three papers and turn in the papers whenever they decided to finish them. Similarly, naïve decision makers would do the same, not anticipating that they would procrastinate completing the papers. Alternatively, sophisticated decision makers may be willing to risk the penalties and set early deadlines simply to commit themselves to finish them.
In fact, the majority of students set binding deadlines: 44 days before the end of the semester for the first paper, 26 days before the end of the semester for the second paper, and 10 days before the end of the semester for the third paper. This suggests that the students understood their tendency to procrastinate and decided to use the commitment mechanism, as Odysseus did, to bind themselves to the mast. However, the authors also found that the students did not set the deadlines in a way that maximized their performance on the papers.
Another group of 48 students were given deadlines specified by the instructor. The students who did not have control over their deadlines did significantly better on the assignments, earning about 3 percentage points more than those who could choose. Perhaps we know we will be behave badly but we do not recognize the full extent of the problem.
