
- •Brief Contents
- •Contents
- •Preface
- •Who Should Use this Book
- •Philosophy
- •A Short Word on Experiments
- •Acknowledgments
- •Rational Choice Theory and Rational Modeling
- •Rationality and Demand Curves
- •Bounded Rationality and Model Types
- •References
- •Rational Choice with Fixed and Marginal Costs
- •Fixed versus Sunk Costs
- •The Sunk Cost Fallacy
- •Theory and Reactions to Sunk Cost
- •History and Notes
- •Rational Explanations for the Sunk Cost Fallacy
- •Transaction Utility and Flat-Rate Bias
- •Procedural Explanations for Flat-Rate Bias
- •Rational Explanations for Flat-Rate Bias
- •History and Notes
- •Theory and Reference-Dependent Preferences
- •Rational Choice with Income from Varying Sources
- •The Theory of Mental Accounting
- •Budgeting and Consumption Bundles
- •Accounts, Integrating, or Segregating
- •Payment Decoupling, Prepurchase, and Credit Card Purchases
- •Investments and Opening and Closing Accounts
- •Reference Points and Indifference Curves
- •Rational Choice, Temptation and Gifts versus Cash
- •Budgets, Accounts, Temptation, and Gifts
- •Rational Choice over Time
- •References
- •Rational Choice and Default Options
- •Rational Explanations of the Status Quo Bias
- •History and Notes
- •Reference Points, Indifference Curves, and the Consumer Problem
- •An Evolutionary Explanation for Loss Aversion
- •Rational Choice and Getting and Giving Up Goods
- •Loss Aversion and the Endowment Effect
- •Rational Explanations for the Endowment Effect
- •History and Notes
- •Thought Questions
- •Rational Bidding in Auctions
- •Procedural Explanations for Overbidding
- •Levels of Rationality
- •Bidding Heuristics and Transparency
- •Rational Bidding under Dutch and First-Price Auctions
- •History and Notes
- •Rational Prices in English, Dutch, and First-Price Auctions
- •Auction with Uncertainty
- •Rational Bidding under Uncertainty
- •History and Notes
- •References
- •Multiple Rational Choice with Certainty and Uncertainty
- •The Portfolio Problem
- •Narrow versus Broad Bracketing
- •Bracketing the Portfolio Problem
- •More than the Sum of Its Parts
- •The Utility Function and Risk Aversion
- •Bracketing and Variety
- •Rational Bracketing for Variety
- •Changing Preferences, Adding Up, and Choice Bracketing
- •Addiction and Melioration
- •Narrow Bracketing and Motivation
- •Behavioral Bracketing
- •History and Notes
- •Rational Explanations for Bracketing Behavior
- •Statistical Inference and Information
- •Calibration Exercises
- •Representativeness
- •Conjunction Bias
- •The Law of Small Numbers
- •Conservatism versus Representativeness
- •Availability Heuristic
- •Bias, Bigotry, and Availability
- •History and Notes
- •References
- •Rational Information Search
- •Risk Aversion and Production
- •Self-Serving Bias
- •Is Bad Information Bad?
- •History and Notes
- •Thought Questions
- •Rational Decision under Risk
- •Independence and Rational Decision under Risk
- •Allowing Violations of Independence
- •The Shape of Indifference Curves
- •Evidence on the Shape of Probability Weights
- •Probability Weights without Preferences for the Inferior
- •History and Notes
- •Thought Questions
- •Risk Aversion, Risk Loving, and Loss Aversion
- •Prospect Theory
- •Prospect Theory and Indifference Curves
- •Does Prospect Theory Solve the Whole Problem?
- •Prospect Theory and Risk Aversion in Small Gambles
- •History and Notes
- •References
- •The Standard Models of Intertemporal Choice
- •Making Decisions for Our Future Self
- •Projection Bias and Addiction
- •The Role of Emotions and Visceral Factors in Choice
- •Modeling the Hot–Cold Empathy Gap
- •Hindsight Bias and the Curse of Knowledge
- •History and Notes
- •Thought Questions
- •The Fully Additive Model
- •Discounting in Continuous Time
- •Why Would Discounting Be Stable?
- •Naïve Hyperbolic Discounting
- •Naïve Quasi-Hyperbolic Discounting
- •The Common Difference Effect
- •The Absolute Magnitude Effect
- •History and Notes
- •References
- •Rationality and the Possibility of Committing
- •Commitment under Time Inconsistency
- •Choosing When to Do It
- •Of Sophisticates and Naïfs
- •Uncommitting
- •History and Notes
- •Thought Questions
- •Rationality and Altruism
- •Public Goods Provision and Altruistic Behavior
- •History and Notes
- •Thought Questions
- •Inequity Aversion
- •Holding Firms Accountable in a Competitive Marketplace
- •Fairness
- •Kindness Functions
- •Psychological Games
- •History and Notes
- •References
- •Of Trust and Trustworthiness
- •Trust in the Marketplace
- •Trust and Distrust
- •Reciprocity
- •History and Notes
- •References
- •Glossary
- •Index

|
|
|
|
Probability Weights without Preferences for the Inferior |
|
239 |
|
EXAMPLE 9.6 Performance Warranty
The evidence from laboratory experiments suggests that people are very poor at dealing with small probabilities. In particular, probability weighting suggests that people treat small-probability events as if they happen much more often than they do. This could potentially lead people to overvalue insurance against very low probability events. For example, many electronic devices come with an option to purchase an extended warranty. This warranty will replace the product should it fail over a particular period of time.
For example, a $400 media player is offered by one prominent retail chain with an optional two-year warranty for $50. The probability of failure for MP3 players is fairly low. Suppose that one in 20 fail in the first two years (the probability cited by the manufacturer of this product). Then the expected cost of replacement is $400 × 0.05 = $20. In this case, the retailer is charging 250 percent of the expected replacement cost! What a profit margin. But why might people be willing to pay so much for such coverage? Suppose people were completely risk neutral, but they behaved according to probability weighting. If the perceived probability of failure π 0.05
0.05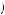 > 0.125, then the buyer would be willing to purchase what is a very unfair insurance policy.
> 0.125, then the buyer would be willing to purchase what is a very unfair insurance policy.
Some insurance and risk-related behaviors suggest other behavioral effects may be at work. For example, many homeowners are unwilling to purchase flood insurance despite relatively low prices and federal subsidies. In this case, people appear to undervalue the insurance offered to them. Similarly, consider individual behavior in purchasing lottery tickets. Lottery tickets sell for much more than their expected payout, yet people continue to buy these tickets on a regular basis. These behaviors appear to be inconsistent with probability weighting. Perhaps with such large rewards or penalties involved, other decision mechanisms take over, much like with the P- and $-bets discussed earlier.
Probability Weights without Preferences for the Inferior
Decisions based on probability weighting predict that people display a preference for stochastically dominated gambles. Suppose, for example, that the probability-weighting function is such that π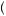 0.9
0.9 = 0.89 and π
= 0.89 and π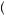 0.1
0.1 = 0.12. Suppose further that the utility function is given by U
= 0.12. Suppose further that the utility function is given by U x
x = lnx. If the gambler’s preferences are described by these functions, then clearly $20 is preferred to $19 (utility of 2.99 vs. 2.94). If instead we considered a gamble (Gamble A) that yields $20 with probability 0.9 and $19 with probability 0.1, we would find utility
= lnx. If the gambler’s preferences are described by these functions, then clearly $20 is preferred to $19 (utility of 2.99 vs. 2.94). If instead we considered a gamble (Gamble A) that yields $20 with probability 0.9 and $19 with probability 0.1, we would find utility
U A = π 0.9 ln20 + π 0.1 ln19 0.89 × 2.99 + 0.12 × 2.94 3.02. |
9 36 |
But this suggests that the gambler would prefer a gamble A to receiving $20 with certainty. Of course this would be madness. No reasonable person would ever trade $20 for a gamble that would produce either $20 or $19. This is because the perceived probabilities are superadditive. In other words, the probability weights sum to more
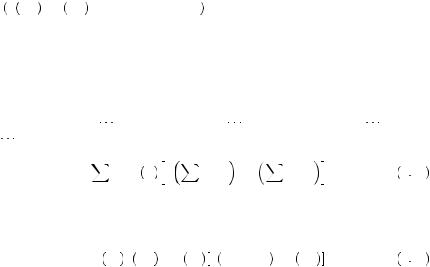
|
|
|
|
|
|
|
|
240 |
|
DECISION UNDER RISK AND UNCERTAINTY |
|
|
|
|
|
than 1 π 0.1 + π 0.9 |
= 0.12 + 0.89 = 1.01 . This superadditivity leads to a perception |
|||
|
|
that the random outcome is better than certainty. Although it is possible to find domi- |
||||
|
|
nated gambles that people will choose, this is generally thought to be due to a non- |
||||
|
|
transparent presentation of the gamble rather than misperception of probabilities. Thus, |
||||
|
|
this property of the weighted probability preferences seems implausible. |
|
|||
|
|
|
John Quiggin proposed a solution to this problem in which probability weights are a |
|||
|
|
function of the rank of the outcome and not just the probability. Suppose that a gamble |
||||
|
|
assigns probabilities p1, |
, pn to outcomes x1, |
, xn, where x1 < x2 < |
< xn for |
|
i = 2, |
, n. Then Quiggin’s rank-dependent expected utility is defined by |
|
||||
|
V = |
n |
U xi π |
i pj − π |
i − 1 pj . |
9 37 |
|
|
i = 1 |
j = 1 |
j = 1 |
|
|
In our example, x1 = 19 and x2 = 20, p1 = 0.1 and p2 = 0.9. Thus, the rank-dependent utility would be given by
V = ln 19 π 0.1 + ln 20 π 0.9 + 0.1 − π 0.1 . |
9 38 |
So long as the weighting function has π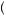 1
1 = 1, the sum of the rank-dependent weights must be 1 (in this case, π
= 1, the sum of the rank-dependent weights must be 1 (in this case, π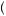 0.1
0.1 + π
+ π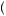 0.9 + 0.1
0.9 + 0.1 − π
− π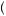 0.1
0.1 = π
= π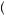 0.9 + 0.1
0.9 + 0.1 = π
= π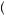 1
1 = 1). Thus, if π
= 1). Thus, if π 1
1 = 1, then the rank-dependent expected utility given in equation 9.38 must be less than U
= 1, then the rank-dependent expected utility given in equation 9.38 must be less than U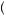 20
20 = ln
= ln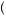 20
20 . To see this, note that V is now identical to the expected utility of a gamble with similar outcomes and the probabilities π
. To see this, note that V is now identical to the expected utility of a gamble with similar outcomes and the probabilities π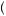 0.1
0.1 and
and  π
π 0.9 + 0.1
0.9 + 0.1 − π
− π 0.1
0.1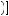 , which must be less than the utility of $20 with certainty. Because the weights sum to 1, they can now represent probabilities in some alternative perceived gamble. The same must hold no matter how many outcomes are possible. Rank-dependent expected utility thus allows nonlinear perception of probabilities but still preserves the preference for stochastically dominating gambles.
, which must be less than the utility of $20 with certainty. Because the weights sum to 1, they can now represent probabilities in some alternative perceived gamble. The same must hold no matter how many outcomes are possible. Rank-dependent expected utility thus allows nonlinear perception of probabilities but still preserves the preference for stochastically dominating gambles.
Practical Implications of Violations
of Expected Utility
For a decision maker, the practical implications of the risky choice literature is clear. When left to their own devices, people have a difficult time dealing with risky choices. When choices become convoluted or otherwise complicated to deal with, people make significant mistakes. Further, people have difficulty in dealing with extreme probabilities. Thus, it is often a good idea for people dealing with risky choices to use morerigorous decision processes. It would be difficult to fall prey to problems such as choosing a dominated gamble if one would use simple calculations of the mean and perhaps the variance of the gambles involved. The primary problem with implementing this advice is that people generally do not observe probabilities. When choosing investments, one may have historical data about previous returns but no credible information about future returns. Using rigorous statistical analysis can lead to much better estimates of probability distributions than simple feelings or perceptions, but they also have biases and statistical problems of their own. Nonetheless, in many situations

|
|
|
|
Practical Implications of Violations of Expected Utility |
|
241 |
|
simple calculations can make choices very clear. For example, when offered an extended warranty on a product, asking yourself the necessary probability of failure in order to make the price of the warranty equal to the expected replacement cost can save you substantial money. If the required probability exceeds reasonable expectations of performance, don’t buy.
From the point of view of firms marketing risky products or risk-management products, it can be a simple matter to increase the demand for products by overemphasizing smallprobability events, emphasizing the possibility of regret, or emphasizing the uniquely attractive properties of a risky choice. The overemphasis of small-probability events should allow substantial profit margins when selling insurance on low-probability risks or when people recognize the possibility of regret from passing up the opportunity to insure. Alternatively, drawing attention to extreme outcomes or extreme probabilities in a choice could appeal to those using a similarity heuristic decision mechanism. Thus, lotteries emphasize and advertise the big winners rather than the odds of winning or the smaller size prizes that may be available.
EXAMPLE 9.7 The Ellsberg Paradox
Suppose you were presented with two urns each containing 100 bingo balls that are either red or black. In the first urn you know that there are 100 balls, and you know that there are only red or black balls in the urn, but you do not know how many of each color. But you are allowed to inspect the second urn, and you find exactly 50 red balls and 50 black balls. You are told you will receive $100 if you draw a red ball and nothing if you draw a black ball. You are then given the choice to draw from either of the urns. Which urn would you choose, and why? Most people in this case decide to choose from the second urn, citing the knowledge of the probabilities of drawing a red ball. Suppose this was your choice. Now suppose that you had instead been given the opportunity to draw and told you would receive $100 if you drew a black ball. Which urn would you choose? Again, most decide to choose the second urn. But such a combination of choices defies the standard axioms of beliefs and probability.
Consider an expected-utility maximizer who chooses the first urn when hoping to draw a red ball. Let us set U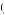 0
0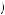 = 0, which we can do without losing general applicability of the result. Then choosing urn 2 implies that
= 0, which we can do without losing general applicability of the result. Then choosing urn 2 implies that
0.50U 100 > pr U 100 |
9 39 |
which implies 0.50 > pr , where pr is the person’s belief regarding the probability of drawing a red ball from the first urn. Alternatively, choosing the second urn when hoping to draw a black ball implies
0.50U 100 > 1 − pr U 100 |
9 40 |
where 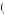 1 − pr
1 − pr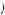 is the person’s belief regarding the probability of drawing a black ball from the first urn. Equation 9.42 implies that 0.50 < pr , contradicting equation 9.41.
is the person’s belief regarding the probability of drawing a black ball from the first urn. Equation 9.42 implies that 0.50 < pr , contradicting equation 9.41.

|
|
|
|
|
242 |
|
DECISION UNDER RISK AND UNCERTAINTY |
There is no set of beliefs conforming to the laws of probability that would lead one to choose the second urn for both of these gambles. Rather, it appears that people make this choice to avoid the ambiguity associated with the first urn rather than forming any beliefs at all.
This paradox, proposed by Daniel Ellsberg in 1961, was designed to examine how people deal with situations where probabilities of the various outcomes are not known to the decision maker. Ten years later, Daniel Ellsberg himself faced a very important decision with high stakes and unknown probabilities of outcomes. His expertise on decision making was put to use in helping to study and advise U.S. strategy and decision making regarding the Vietnam War. While working with background documents he became convinced that each of three presidential administrations had deceived the public regarding the conduct of the war and the prospects to win. Without the electorate’s having full information, the president was pressured to escalate a war that he believed was unwinnable. Ellsberg faced the choice to either make public the secret documents he had access to and lay bare the deceit or to keep these documents secret. Should he keep the documents secret, he would likely keep his job, and the war would escalate, resulting in continued loss of life. Should he go public with the documents, the war might stop, but he would likely lose his job and could be prosecuted for treason, resulting in a minimum of jail time and perhaps death.
In 1971, he contacted the New York Times and passed the documents to the paper for publication. The Pentagon Papers exposed several instances of deceit under several administrations—most notably the Johnson administration—and helped lead to a U.S. withdrawal from Vietnam under President Nixon. The Nixon administration brought several charges against Ellsberg, threatening up to 115 years in prison. The charges were later thrown out by the courts, partially owing to several extralegal methods employed by the Nixon administration in gathering evidence. In what may be seen as poetic justice, two of the charges against President Nixon in his impeachment proceedings stemmed from his treatment of Daniel Ellsberg.
What to Do When You Don’t Know
What Can Happen
The phenomenon on display in the Ellsberg paradox is often referred to as ambiguity aversion. Ambiguity aversion is displayed when a decision maker tends to choose options for which the information about probabilities and outcomes is explicit, over options for which either the probabilities or outcomes are unknown or ambiguous. For the purposes of this book, we explicitly examine cases in which the possible outcomes are known (or at least believed to be known) but the probability of each of those outcomes is unknown. We will refer to such a cases as displaying ambiguity or uncertainty. At the heart of ambiguity aversion is the necessity of holding (at least) two sets of inconsistent beliefs simultaneously. Rational theory (in this case called subjective expected utility theory) suggests we should hold one set of beliefs about the probability of drawing a red ball from the first urn, that these beliefs should satisfy standard laws of probability, and that all of our decisions should be based upon that set of beliefs. In the

|
|
|
|
What to Do When You Don’t Know What Can Happen |
|
243 |
|
Ellsberg paradox, people display ambiguity aversion because they behave as if pr < 0.5 when they hope to draw a red ball and as if pr > 0.5 when they hope to draw a black ball. A procedurally rational model of decision under uncertainty was proposed by Itzhak Gilboa and David Schmeidler, supposing that people choose the option that displays the best of the worst possible set of probabilities, called the maxmin expected utility theory of choice under ambiguity. Suppose that P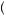 x
x represented the set of possible beliefs that one could hold regarding the outcomes of choosing action x. Further, let
represented the set of possible beliefs that one could hold regarding the outcomes of choosing action x. Further, let  p
p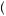 y
y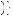 represent one possible probability distribution of outcomes y when choosing action x. Then someone who behaves according to maxmin expected utility theory will choose
represent one possible probability distribution of outcomes y when choosing action x. Then someone who behaves according to maxmin expected utility theory will choose
maxx min p y P x |
p y U y . |
9 41 |
|
y |
|
Thus, people choose the action such that they will be the best off in the event that the worst possible set of probabilities prevail. An illustration may be helpful.
Suppose that Noor faces a choice between gamble A and gamble B. Gamble A would result in $100 with probability pA, with p0 ≤ pA ≤ p1, and $0 with the remaining probability. Gamble B would result in $50 with probability pB, with p2 ≤ pB ≤ p3, and $0 with the remaining probability. Then Noor will value gamble A according to
V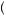 A
A = minpA
= minpA p0, p1
p0, p1 pAU
pAU 100
100 +
+  1 − pA
1 − pA U
U 0
0 = p0U
= p0U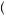 100
100 +
+  1 − p0
1 − p0 U
U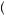 0
0 .
. 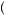 9
9 42
42
In other words, the decision maker supposes that the worst set of possible probabilities are correct. Noor will evaluate gamble B according to
V A = minpB p2, p3 pBU 50 + 1 − pB U 0 = p2U 50 + 1 − p2 U 0 . |
9 43 |
Then Noor will choose A if V A > V B , or |
|
p0U 100 + 1 − p0 U 0 > p2U 50 + 1 − p2 U 0 . |
9 44 |
Essentially, a maxmin expected utility maximizer assumes the worst of every gamble. Here, the worst possible beliefs regarding gamble A, or those producing the lowest utility, are pA = p0. Similarly, the worst beliefs for gamble B are pB = p2. The decision maker then chooses based upon these worst-case scenarios. Casting this into the framework of equation 9.41, the possible actions, x, are the choices of either A or B. The possible outcomes, y, are either $100 or $0 in the case of A, or $50 and $0 in the case of B. The set of probabilities, P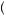 x
x , are
, are 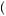 p0, p1
p0, p1 for x = A, and
for x = A, and  p2, p3
p2, p3 for x = B.
for x = B.
If we consider the case of the Ellsberg paradox, the choice of urn 2 corresponds to
V Urn 2 = 0.50U 100 + 0.5U 0 |
9 45 |
because we are told explicitly that half of the balls are red and half are black. We are not told the number of red and black balls in urn 1. There may be no red balls. Thus, the value of urn 1 is given by
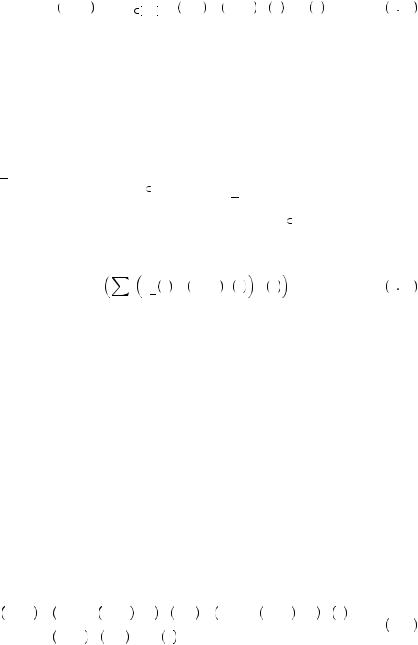
|
|
|
|
|
244 |
|
DECISION UNDER RISK AND UNCERTAINTY |
V Urn1 = minp 0, 1 pU 100 + 1 − p U 0 = U 0 |
9 46 |
Clearly, urn 2 is superior to urn 1 in this case. If we then thought about making the same choice when a black ball will result in a reward, the calculation is the same. We haven’t been told the probability, and for all we know there may be no black balls. Thus, equation 9.46 still holds.
A more general model of decision under ambiguity was proposed by Paolo Ghirardato, Fabio Maccheroni, and Massimo Marinacci, called α-maxmin expected utility theory. Their theory is based on the notion that the degree to which the decision maker gives weight to the worst possible beliefs represents just how averse to ambiguity the person may be. Let 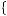 p
p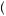 y
y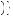 be the set of beliefs for a given action that results in the minimum expected utility, or the solution to arg min
be the set of beliefs for a given action that results in the minimum expected utility, or the solution to arg min p
p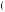 y
y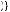 P
P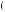 x
x
 yp
yp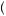 y
y U
U y
y (the probabilities corresponding to the solution to the maxmin problem). Further, define
(the probabilities corresponding to the solution to the maxmin problem). Further, define  p
p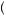 y
y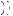 as the set of beliefs that results in the maximum expected utility, or the solution to arg max
as the set of beliefs that results in the maximum expected utility, or the solution to arg max p
p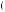 y
y P
P x
x
 y p
y p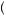 y
y U
U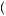 y
y (these are the probabilities that correspond to the best possible expected utility). Then an α-maxmin expected-utility maximizer will behave according to
(these are the probabilities that correspond to the best possible expected utility). Then an α-maxmin expected-utility maximizer will behave according to
maxx |
αp y + 1 − α |
|
y U y , |
9 47 |
p |
||||
|
y |
|
||
where α 
 0, 1
0, 1 . Here α can be considered an index of ambiguity aversion. The more ambiguity averse, the closer α is to 1. Someone with α > 12 is considered to be ambiguity averse, and someone with α < 12 is considered to be ambiguity loving. This model reduces to the maxmin expected-utility model when α = 1, resulting in the person’s reacting only to the worst possible beliefs for a given choice. If α = 12, the perceived probability of each event will be exactly 1/2 the probability from the maxmin solution plus 1/2 the probability from the maximum expected-utility solution. In the simple case of two possible outcomes, the subjective probabilities will be the same even if outcomes are swapped (as in rewarding the drawing of a black ball rather than a red ball). This means preferences will satisfy the subjective expected utility model. We will refer to α as the coefficient of ambiguity aversion.
. Here α can be considered an index of ambiguity aversion. The more ambiguity averse, the closer α is to 1. Someone with α > 12 is considered to be ambiguity averse, and someone with α < 12 is considered to be ambiguity loving. This model reduces to the maxmin expected-utility model when α = 1, resulting in the person’s reacting only to the worst possible beliefs for a given choice. If α = 12, the perceived probability of each event will be exactly 1/2 the probability from the maxmin solution plus 1/2 the probability from the maximum expected-utility solution. In the simple case of two possible outcomes, the subjective probabilities will be the same even if outcomes are swapped (as in rewarding the drawing of a black ball rather than a red ball). This means preferences will satisfy the subjective expected utility model. We will refer to α as the coefficient of ambiguity aversion.
To illustrate, consider again the Ellsberg paradox. The value of urn 2 will continue to be as given in equation 9.45 because the probabilities were explicitly given in this case. In the case of urn 1, the probability of obtaining $100 can be anywhere between 0 and 1. The best-case beliefs—those that produce the highest expected utility—would be p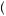 100
100 = 1, and the worst-case beliefs would be p
= 1, and the worst-case beliefs would be p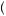 100
100 = 0. Thus, the decision maker would value urn 1 according to
= 0. Thus, the decision maker would value urn 1 according to
V Urn1 = α × 0 + 1 − α × 1 U 100 + α × 1 + 1 − α × 0 U 0
9 48
48
= 1 − α U 100 + αU 0
Comparing this to equation 9.45, the person will choose urn 1 if α < 12, implying ambiguity-loving behavior. In this case, the person assumes the outcome is closer to the more optimistic beliefs. The person will choose urn 2 if α > 12, implying ambiguity aversion. With α > 12, the person believes the outcomes will be closer to the
|
|
|
|
What to Do When You Don’t Know What Can Happen |
|
245 |
|
more-pessimistic beliefs. Finally, if α = 12, the person is indifferent between the two urns—reflecting the lack of information about urn 1. Some of the experimental evidence suggests that people behave ambiguity loving over losses and ambiguity averse over gains. Such a possibility suggests a very close association between ambiguity aversion and risk aversion behavior.
EXAMPLE 9.8 Ambiguity in Policymaking
Ambiguity is relatively pervasive in many contexts where we may be considering a new technology, regulation, or change in strategy. Consider a deadly disease that has a 3/4 chance of killing anyone infected when given the accepted treatment. Alternatively, a new treatment has been proposed. The new treatment has not been fully tested through clinical trials, but researchers believe that it will result in probability of survival in the range of p 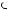 p, p . The regulatory board that approves clinical trials is ambiguity averse, with a coefficient of ambiguity aversion equal to α. The regulatory board is considering approving a trial of the new treatment. Suppose that the board derives U
p, p . The regulatory board that approves clinical trials is ambiguity averse, with a coefficient of ambiguity aversion equal to α. The regulatory board is considering approving a trial of the new treatment. Suppose that the board derives U Survive
Survive = 100 if a patient survives after treatment and U
= 100 if a patient survives after treatment and U Death
Death = 0 if a patient dies after treatment. Thus, the regulatory board values the current treatment according to expected utility theory
= 0 if a patient dies after treatment. Thus, the regulatory board values the current treatment according to expected utility theory
V Current Treatment = 0.25 × U Survive + 0.75 × U Death = 25. |
9 49 |
Alternatively, the new treatment results in ambiguity. In this case, if the regulatory council knew the probability of survival under the new treatment, they would value the new treatment as
V New Treatment = p × U Survive + 1 − p × U Death = 100p, |
9 50 |
with maxp 100p = 100p, and minp 100p = 100p. Thus, the regulatory board will value the ambiguous prospect of using the new treatment as
100 αp + 1 − α |
|
. |
9 51 |
||||
p |
|||||||
|
|
|
|
|
αp + 1 − α |
|
|
Thus, the new treatment will only be approved for trial if 25 < 100 |
|
, or |
|||||
p |
|||||||
.25 < αp +  1 − α
1 − α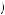 p . If the board is fully ambiguity averse, then α = 1, and they will only approve the new trial if p > 0.25. In other words, it will only proceed to trial if it is guaranteed to reduce the probability of death. Alternatively, if the regulatory board is fully ambiguity loving, they will approve the trial if p > 0.25. In other words it will be approved if there is any chance that the new treatment could reduce the probability of death. Finally, if we consider α = 0.5, then the regulatory board will approve the trial if
p . If the board is fully ambiguity averse, then α = 1, and they will only approve the new trial if p > 0.25. In other words, it will only proceed to trial if it is guaranteed to reduce the probability of death. Alternatively, if the regulatory board is fully ambiguity loving, they will approve the trial if p > 0.25. In other words it will be approved if there is any chance that the new treatment could reduce the probability of death. Finally, if we consider α = 0.5, then the regulatory board will approve the trial if
.5 < p + p. Thus, if the best possible probability is above 0.25 by at least as much as the worst possibility is below it, then the trial will be approved.
Ambiguity aversion in this case would lead the regulatory board to restrict new trials even if there is a substantial promise of better outcomes. Ambiguity aversion has also been used to describe government response to food safety scares and emissions regulation in the face of global climate change. In each of these cases, ambiguity aversion leads the government toward overregulation owing to the possibility of catastrophic outcomes.
