
- •Brief Contents
- •Contents
- •Preface
- •Who Should Use this Book
- •Philosophy
- •A Short Word on Experiments
- •Acknowledgments
- •Rational Choice Theory and Rational Modeling
- •Rationality and Demand Curves
- •Bounded Rationality and Model Types
- •References
- •Rational Choice with Fixed and Marginal Costs
- •Fixed versus Sunk Costs
- •The Sunk Cost Fallacy
- •Theory and Reactions to Sunk Cost
- •History and Notes
- •Rational Explanations for the Sunk Cost Fallacy
- •Transaction Utility and Flat-Rate Bias
- •Procedural Explanations for Flat-Rate Bias
- •Rational Explanations for Flat-Rate Bias
- •History and Notes
- •Theory and Reference-Dependent Preferences
- •Rational Choice with Income from Varying Sources
- •The Theory of Mental Accounting
- •Budgeting and Consumption Bundles
- •Accounts, Integrating, or Segregating
- •Payment Decoupling, Prepurchase, and Credit Card Purchases
- •Investments and Opening and Closing Accounts
- •Reference Points and Indifference Curves
- •Rational Choice, Temptation and Gifts versus Cash
- •Budgets, Accounts, Temptation, and Gifts
- •Rational Choice over Time
- •References
- •Rational Choice and Default Options
- •Rational Explanations of the Status Quo Bias
- •History and Notes
- •Reference Points, Indifference Curves, and the Consumer Problem
- •An Evolutionary Explanation for Loss Aversion
- •Rational Choice and Getting and Giving Up Goods
- •Loss Aversion and the Endowment Effect
- •Rational Explanations for the Endowment Effect
- •History and Notes
- •Thought Questions
- •Rational Bidding in Auctions
- •Procedural Explanations for Overbidding
- •Levels of Rationality
- •Bidding Heuristics and Transparency
- •Rational Bidding under Dutch and First-Price Auctions
- •History and Notes
- •Rational Prices in English, Dutch, and First-Price Auctions
- •Auction with Uncertainty
- •Rational Bidding under Uncertainty
- •History and Notes
- •References
- •Multiple Rational Choice with Certainty and Uncertainty
- •The Portfolio Problem
- •Narrow versus Broad Bracketing
- •Bracketing the Portfolio Problem
- •More than the Sum of Its Parts
- •The Utility Function and Risk Aversion
- •Bracketing and Variety
- •Rational Bracketing for Variety
- •Changing Preferences, Adding Up, and Choice Bracketing
- •Addiction and Melioration
- •Narrow Bracketing and Motivation
- •Behavioral Bracketing
- •History and Notes
- •Rational Explanations for Bracketing Behavior
- •Statistical Inference and Information
- •Calibration Exercises
- •Representativeness
- •Conjunction Bias
- •The Law of Small Numbers
- •Conservatism versus Representativeness
- •Availability Heuristic
- •Bias, Bigotry, and Availability
- •History and Notes
- •References
- •Rational Information Search
- •Risk Aversion and Production
- •Self-Serving Bias
- •Is Bad Information Bad?
- •History and Notes
- •Thought Questions
- •Rational Decision under Risk
- •Independence and Rational Decision under Risk
- •Allowing Violations of Independence
- •The Shape of Indifference Curves
- •Evidence on the Shape of Probability Weights
- •Probability Weights without Preferences for the Inferior
- •History and Notes
- •Thought Questions
- •Risk Aversion, Risk Loving, and Loss Aversion
- •Prospect Theory
- •Prospect Theory and Indifference Curves
- •Does Prospect Theory Solve the Whole Problem?
- •Prospect Theory and Risk Aversion in Small Gambles
- •History and Notes
- •References
- •The Standard Models of Intertemporal Choice
- •Making Decisions for Our Future Self
- •Projection Bias and Addiction
- •The Role of Emotions and Visceral Factors in Choice
- •Modeling the Hot–Cold Empathy Gap
- •Hindsight Bias and the Curse of Knowledge
- •History and Notes
- •Thought Questions
- •The Fully Additive Model
- •Discounting in Continuous Time
- •Why Would Discounting Be Stable?
- •Naïve Hyperbolic Discounting
- •Naïve Quasi-Hyperbolic Discounting
- •The Common Difference Effect
- •The Absolute Magnitude Effect
- •History and Notes
- •References
- •Rationality and the Possibility of Committing
- •Commitment under Time Inconsistency
- •Choosing When to Do It
- •Of Sophisticates and Naïfs
- •Uncommitting
- •History and Notes
- •Thought Questions
- •Rationality and Altruism
- •Public Goods Provision and Altruistic Behavior
- •History and Notes
- •Thought Questions
- •Inequity Aversion
- •Holding Firms Accountable in a Competitive Marketplace
- •Fairness
- •Kindness Functions
- •Psychological Games
- •History and Notes
- •References
- •Of Trust and Trustworthiness
- •Trust in the Marketplace
- •Trust and Distrust
- •Reciprocity
- •History and Notes
- •References
- •Glossary
- •Index
|
|
|
|
Rational Prices in English, Dutch, and First-Price Auctions |
|
105 |
|
When David Lucking-Reiley conducted a set of experiments by auctioning off Magic: The Gathering trading cards in a series of Internet auctions (see Example 5.3), he also auctioned off 175 cards each in Dutch and first-price auctions. In the end he found substantially higher bids in the Dutch than in the first-price auctions, in line with the anchoring and adjustment prediction. In fact, the bid price per card increased by about $0.30 when using the Dutch versus the first-price auction on cards that are valued at about $3 apiece. It is difficult to say why laboratory experiments have produced such different results from the field experiment. One possible reason is that real-life auctions draw a particular type of person who might differ from those likely to participate in a laboratory experiment. In this case, however, those choosing to participate in the realworld auctions fall prey to an errant anchor.
History and Notes
Auctions have long been used to determine prices for rare objects or objects that are difficult to price as a commodity. The Dutch auction became famous as a mechanism for flower auctions in Holland in the early seventeenth century. At the time, tulips had recently been introduced into Europe. Their vibrant colors and novelty created a fervent interest in the new flower. Because there were very few tulip bulbs relative to the number who wanted to buy, it became a practice to sell the bulbs at auction to the highest bidder, giving rise to the Dutch auction. From about 1634 to 1637 the auction prices for bulbs soared by several hundred percent, with the top prices for a single bulb of 5,200 Guilder, the equivalent of several hundred thousand dollars today. This steep and seemingly unrealistic rise in the price of tulip bulbs was dubbed “tulipomania.” Investors purchased the bulbs expecting to resell them for a quick profit. In 1637, participants in a Haarlem auction failed to bid at the levels investors had come to expect. News spread quickly and spooked those holding bulbs. The price quickly dropped nearly 100 percent, and the Dutch government suspended trade in all tulips. Although it seems unlikely to be a primary factor, perhaps the Dutch auction mechanism itself played a role in setting initially high prices where the steady stream of new and inexperienced bidders might have anchored on high starting auction prices, resulting in overly high bids and thus increasing prices.
Rational Prices in English, Dutch,
and First-Price Auctions
Although there are no good reasons why bids in the first-price and Dutch auctions should differ, or why anyone would ever bid above their valuation, there are some rational
|
|
|
|
|
106 |
|
THE WINNER’S CURSE AND AUCTION BEHAVIOR |
explanations for why the Dutch and first-price auctions might produce realized prices that are above those in second-price auctions. In the derivation of the optimal bids in this chapter we have assumed that people maximize the expected payout. This assumption eliminates the possibility that people might value less-risky choices over riskier choices, called risk aversion. For example, a strategy that has a 50 percent chance of resulting in a payoff of five cents and a 50 percent chance of resulting in a loss of five cents has an expected payout of $0. Suppose an alternative strategy were available that offered a 50 percent chance of obtaining $1,000,000 and a 50 percent chance of losing $1,000,000. This also has an expected payout of $0, but many might be more inclined to choose the lower-stakes strategy because it offers less risk. More generally, risk preferences are often represented by a utility of money function, u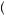 π
π , so that people maximize the expected utility of their payout rather than the expected payout itself. If the utility function is increasing and displays diminishing marginal utility of payout (in other words, it is a concave function), then the consumer prefers lower levels of risk given the same expected payout (this is discussed in greater detail in Chapter 6).
, so that people maximize the expected utility of their payout rather than the expected payout itself. If the utility function is increasing and displays diminishing marginal utility of payout (in other words, it is a concave function), then the consumer prefers lower levels of risk given the same expected payout (this is discussed in greater detail in Chapter 6).
In the Vickrey and English auctions, the dominant strategy still prevails if bidders maximize their expected utility. In these auctions, bidding your valuation is always the optimal bid no matter what the behavior of others, and it thus involves no uncertainty. Alternatively, in the Dutch and first-price auctions, there is no dominant strategy and each possible bid involves some level of uncertainty. Although both the Dutch and English auctions should result in the same behavior, risk aversion might lead to higher bids. In essence, higher bids reduce the payout in the event of winning the auction, while increasing the probability of a win, making the bid safer. On the other hand, no matter what the bid, the payout in the event of a loss is 0. Thus, bidding higher than the riskneutral (or expected payout-maximizing) bid can reduce the risk involved in bidding at a cost of some reduction in expected payout. Aversion to risk can induce bids that are somewhat higher than the bids in the Nash equilibrium we have discussed. Further, the risk-neutral bids in the first-price and Dutch auctions generally result in the same expected price for the item being auctioned as in the Vickrey and English auctions. Thus, risk aversion can lead to higher prices in the Dutch and first-price sealed-bid auctions in general, as has been observed. Despite this, many properties of the observed bids are inconsistent with risk aversion or any sort of Nash equilibrium strategy.
Auction with Uncertainty
Consider a different type of uncertainty in auctions. Suppose, for example, that the bidder wishes to bid on an object so that he can sell it to a third party at a later date. He may be uncertain of the price he will be able to obtain for the item in the future. Thus, it may be that the bidder is uncertain about his own valuation of the item. In addition, some objects have some intrinsic value that is common to all involved. For example, when bidding on an oil well, generally all bidders may be uncertain regarding the actual amount of oil in the well, but all are agreed that it is the value of the oil in the market that determines the value of the well. In this case, valuation is not subjective because the object will not be consumed by the bidder but will be used to derive some monetary value (e.g., through sale on a market). This is called a common-value auction. In a common-value auction, different bidders might have differing estimates or beliefs

|
|
|
|
Rational Bidding under Uncertainty |
|
107 |
|
regarding the eventual value of the item they are bidding on and must form a bid without knowing for certain the value they will obtain. In this case, the estimate of the value plays a significant role. Auctions that are commonly thought of as common-value auctions include oil lease contracts, bidding for free agents in professional sports, or bidding for the rights to publish highly anticipated books (e.g., biographies of recent presidents or their counselors).
Rational Bidding under Uncertainty
Suppose n bidders are engaged in a first-price auction for an item of common value v that is unknown to each individual bidder. Further, suppose that each bidder i obtains a different estimate of v, which we will label vi. For example, the general manager of a major league baseball team might use prior performance to guess the value of a baseball player approaching free agency. The true valuation is not known, but let us suppose that each estimated valuation is drawn at random from a distribution that can be described by a probability function p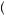 v
v , where v must be in the set
, where v must be in the set  v − k
v − k 2,
2, 

 , v + k
, v + k 2
2 , k is some positive even integer, and the average value of the estimates is E
, k is some positive even integer, and the average value of the estimates is E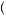 v
v = v. Then each bidder must formulate a bid to solve
= v. Then each bidder must formulate a bid to solve
max E π , |
|
5 10 |
x |
|
|
where |
|
|
πi = v − p if |
xi = p |
5 11 |
0 if |
xi < p, |
|
subject to the strategy of all other bidders.
The problem here is that bidders need to know how to use their imperfect signal of the underlying value in compiling the optimal bid. Given that one has received the signal vi, this value could be as much as k 2 above the true valuation or as much as k
2 above the true valuation or as much as k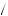 2 below the true value. The probability that vi is k
2 below the true value. The probability that vi is k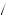 2 above v is p
2 above v is p v + k
v + k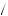 2
2 , and the probability that vi is k
, and the probability that vi is k 2 − 1 greater than v is p
2 − 1 greater than v is p v + k
v + k 2 − 1
2 − 1 , and so on. Thus, the bidder receiving the signal vi, might view the probability function as representing their beliefs regarding the placement of the true value of winning the auction. If the probability that vi is k
, and so on. Thus, the bidder receiving the signal vi, might view the probability function as representing their beliefs regarding the placement of the true value of winning the auction. If the probability that vi is k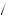 2 above v is p
2 above v is p v + k
v + k 2
2 , then to the bidder, the probability that v = vi − k
, then to the bidder, the probability that v = vi − k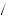 2 is equal to p
2 is equal to p v + k
v + k 2
2 . Thus, the signal produces a probability distribution over possible valuations.
. Thus, the signal produces a probability distribution over possible valuations.
This distribution also tells the bidder about the possible estimates received by others in the auction. For example, if bidder i receives estimate vi, then the probability that bidder j receives valuation vj = vi − k is equal to p v + k
v + k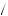 2
2
 p
p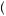 v − k
v − k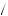 2
2 . To see this, note that given the probability function specified, the only way vj could fall k below vi is if vi = v + k
. To see this, note that given the probability function specified, the only way vj could fall k below vi is if vi = v + k 2 and vj = v − k
2 and vj = v − k 2. If we assume that each estimate is an independent draw from the distribution, then the probability of drawing vi = v + k
2. If we assume that each estimate is an independent draw from the distribution, then the probability of drawing vi = v + k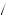 2 and vj = v − k
2 and vj = v − k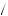 2 is just the product of the probabilities of each individual draw. On the other hand, the proba-
2 is just the product of the probabilities of each individual draw. On the other hand, the proba-
bility that vj = vi − k + 1 is p v + k |
2 p v − k 2 + 1 |
+ p v + k |
2 − 1 p v − k 2 . In |
this case, there are two possible |
ways to obtain a |
difference |
of k − 1 between the |
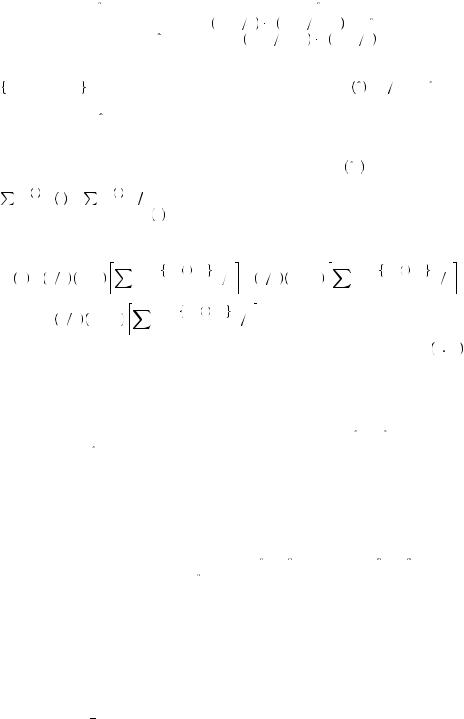
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
108 |
|
THE WINNER’S CURSE AND AUCTION BEHAVIOR |
|
|
|
|
|
|||||
|
|
estimates. Either vi is the highest possible estimate and vj is one above the lowest |
|||||||||||
|
|
possible estimate (with a probability of p v + k |
2 |
p v − k |
2 + 1 ), or vi is one below the |
||||||||
|
|
highest possible estimate and vj is the lowest p v + k |
2 − 1 |
p v − k |
2 . The probability |
||||||||
|
|
that either one of these events happens is the sum of the probability of each event. |
|||||||||||
|
|
|
As |
a simple |
example, |
suppose that |
there |
are |
three possible |
estimates, |
|||
|
|
|
v − 1, v, v + 1 |
, with a uniform probability distribution, so that p v |
= 1 3 that v takes |
||||||||
|
|
on any of these three values, and that n = 2. Suppose bidder 1 draws an estimate of the |
|||||||||||
|
|
value of the good, v1 = 10. Then, the true value is either 9, 10, or 11, with the probability |
|||||||||||
|
|
of each outcome being 1/3. Further, the possible estimates that could be drawn by bidder 2 |
|||||||||||
|
|
are 8, 9, 10, 11, or 12. To find the Nash equilibrium, suppose that bidder 1 believes that |
|||||||||||
|
|
the other bidder will form his bid according to some rule x2 = b v2 |
. Given a true val- |
||||||||||
|
|
uation of v, the probability that a particular bid of x is higher than bidder 2’s bid is |
|||||||||||
|
|
|
b − 1 |
x |
b |
− 1 x |
|
|
|
|
|
|
|
|
|
|
j = v − 1 p j = |
j = v − 1 1 3, where v − 1 is the lowest possible estimate an opponent |
|||||||||
|
|
could draw given v, and b − 1 x |
is the valuation of an opponent that would result in a bid |
||||||||||
|
|
of x. In this event, the expected payout from bidding x is given by |
|
|
|||||||||
|
|
|
E π = 1 3 9−x |
t =max |
b−1 x , 10 |
|
|
|
t =max b−1 |
x , 11 |
|||
|
|
|
t =8 |
1 3 |
+ 1 3 10−x |
9 |
1 3 |
||||||
|
|
|
|
|
|
|
|
|
|
t = |
|
||
|
|
|
|
+ 1 3 |
|
t =max b−1 x , 12 |
|
, |
|
|
|
|
|
|
|
|
|
11−x |
1 3 |
|
|
|
|
||||
|
|
|
|
|
|
t =10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 12 |
where the first term on the right side of the equation is the benefit to the bidder given the possible true value, v = 9, multiplied by the probability that v = 9, (1/3), and the probability that the bid x will win. The second and third terms are constructed similarly for the case where v = 10 and v = 11, respectively. Suppose that b v2
v2 = v2 − 1, so that b − 1
= v2 − 1, so that b − 1 x
x = x + 1 = v. Then, bidding 9 in this case would yield E
= x + 1 = v. Then, bidding 9 in this case would yield E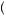 π
π = 1
= 1 9, bidding 10 would yield E
9, bidding 10 would yield E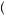 π
π = − 1
= − 1 9, and bidding 11 would yield E
9, and bidding 11 would yield E π
π = − 1. Further, bidding slightly less than 9 yields a lower expected payout by eliminating the possibility of winning if v > 9, and resulting in only a small (less than 1) payout in the event of v = 9. Thus, the expected value for bidding less than 9 would be smaller than 1/9. Bidding slightly above 9 increases the potential price of winning without increasing the possibility of a win and thus results in a lower expected payout. Thus, the optimal bid when faced with an opponent who bids according to b
= − 1. Further, bidding slightly less than 9 yields a lower expected payout by eliminating the possibility of winning if v > 9, and resulting in only a small (less than 1) payout in the event of v = 9. Thus, the expected value for bidding less than 9 would be smaller than 1/9. Bidding slightly above 9 increases the potential price of winning without increasing the possibility of a win and thus results in a lower expected payout. Thus, the optimal bid when faced with an opponent who bids according to b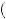 vj
vj = vj − 1 is to bid b
= vj − 1 is to bid b v1
v1 = v1 − 1. The same can be shown for any possible vi, and thus bidding one below the estimated value constitutes a Nash equilibrium in this case.
= v1 − 1. The same can be shown for any possible vi, and thus bidding one below the estimated value constitutes a Nash equilibrium in this case.
This strategy eliminates the possibility of overbidding. By subtracting one from the received estimate, the bid is below the estimate by the maximum possible error in the bid. By receiving an estimate of 10, one immediately knows that the lowest possible valuation is 9. Thus, one guarantees oneself a nonnegative payoff by bidding 9. If both bidders bid 1 below their valuation, the bidder who draws the higher valuation wins the auction.
Suppose that the true value of the object, v, is drawn from a uniform distribution over the set  v, v
v, v and that the estimates of valuation are drawn from a continuous
and that the estimates of valuation are drawn from a continuous
|
|
|
|
Rational Bidding under Uncertainty |
|
109 |
|
uniform distribution, with the support of v being given by participating in the auction, the Nash equilibrium bid in is given by1
 v − ε, v + ε
v − ε, v + ε . With n bidders the common-value auction
. With n bidders the common-value auction
b v = v − ε + |
2ε |
|
e − N 2ε v − v + ε . |
5 13 |
|
N + |
1 |
||||
|
|
|
Thus, the rational model predicts that people bid their value, minus a correction term that reduces the probability of overbidding, plus another correction term that adjusts the bid up if the estimated valuation is improbably low. The second correction term becomes very small as the valuation estimate moves above v + ε. Because this term is likely to be very small for the bidder obtaining the highest estimate of value, the highest bidder’s expected payoff is v − b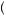 v
v = v − v − ε + ε − N2+ε 1 e −
= v − v − ε + ε − N2+ε 1 e − 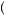 2Nε
2Nε
 v −
v −  v + ε
v + ε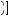
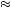 2ε
2ε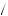 n, which must be positive. Also, both correction terms become smaller as the number of bidders increases, thus raising bids closer to the estimated valuation. The work of Robert Wilson has shown that if the information about the valuation of the good is drawn independently by each bidder from the same distribution and that this distribution is actually a nontrivial function of the true value of the good, the highest bid is very close to the true value of the item. Each bidder must expect nonnegative profits on average in the Nash equilibrium, otherwise it would be in their best interest to place a lower bid. In fact, the highest bid that conforms to equation 5.13 occurs when the highest valuation estimate is drawn, v = v + ε, and the number of bidders, N, tends toward infinity. In this case the bid converges to v. Thus, no one should ever bid above the true underlying value under this framework.
n, which must be positive. Also, both correction terms become smaller as the number of bidders increases, thus raising bids closer to the estimated valuation. The work of Robert Wilson has shown that if the information about the valuation of the good is drawn independently by each bidder from the same distribution and that this distribution is actually a nontrivial function of the true value of the good, the highest bid is very close to the true value of the item. Each bidder must expect nonnegative profits on average in the Nash equilibrium, otherwise it would be in their best interest to place a lower bid. In fact, the highest bid that conforms to equation 5.13 occurs when the highest valuation estimate is drawn, v = v + ε, and the number of bidders, N, tends toward infinity. In this case the bid converges to v. Thus, no one should ever bid above the true underlying value under this framework.
EXAMPLE 5.5 Oil Lease Contracts
The right to drill for oil offshore is typically auctioned off by the government using either first-price or second-price sealed-bid auctions. Oil companies bid for the right to drill, basing their bids on estimates of the amount of oil in the particular region. These estimates are produced by geologists working for the individual company considering a bid.
In 1971, three physicists who had been working in the petroleum industry noted the extremely low profitability of oil lease contracts in the Gulf of Mexico. They noted that the returns from 1950 to the late 1960s were about that of a credit union—extremely low. They thought this occurred because in an auction for a good with an uncertain value, the highest bidder is the bidder with the highest probability of having overestimated the value of the good. Thus, this highest bidder is the one most likely to have overbid and to be turning a loss on the lease. In fact, Capen, Clapp, and Campbell found that often the highest bid is more than four times the second-highest bid, suggesting that the highest bidder was in fact overestimating the value of the oil in the well.
1 This formula must be modified somewhat if the signal is in ε of v or v. I ignore these special cases in the text. See John Kagel and Jean-Francois Richard for more details.

|
|
|
|
|
110 |
|
THE WINNER’S CURSE AND AUCTION BEHAVIOR |
Walter Mead, Asbjorn Moseidjord, and Philip Sorensen found that over the same period, an oil lease yielded an average net present value of −$192,128. In fact, 78 percent of all oil leases resulted in either no oil (the vast majority) or not enough oil to offset the costs of exploration and lease. However, the small number that did produce profits had high returns, leading to overall returns that were about average for all industries in the United States. Further research has suggested that the high-returning leases have resulted from firms placing bids on adjacent lands that they might have had additional information regarding. Those bidding on single leases not adjacent to their own land tend to have much smaller average returns on the lease, suggesting that they might not be realizing the expected return. This means those bidding on oil leases do not appear to be following a Nash equilibrium strategy.
EXAMPLE 5.6 Free Agents in Sports
Bidding wars often erupt in professional sports over the biggest and most recognizable names. In Major League Baseball, any player who has played for at least six years in the league at the time his current contract expires becomes a free agent. This means that he has the opportunity to negotiate a contract with any team he likes. Eligible players declare their free agency on October 15, and subsequently interested teams begin the bidding process. Because the bids of any particular team are generally secret, and the commodity is valued primarily for his playing ability, this can function somewhat like the common-value first-price auction with uncertainty.
James Cassing and Richard Douglas examined the resulting pay for free agents, finding that they are substantially overpaid. They first estimated the marginal revenue product of a point of overall team slugging average (total number of bases on hits divided by total at bats) as well as the ratio of strikeouts to walks. They then compared the free agent’s pay to productivity of slugging and ratio of strikeouts to walks. Of the 44 free agents they examined, 28 were overpaid. Those overpaid were paid an average of 20 percent more than their value to the team. Because the overpayments are so astoundingly high, free agents as a whole are paid more than they are worth on average.
Similar results have been found in auctions for the rights to publish books. When a famous person is intent on writing a book, book publishers sometimes bid on the rights to publish the book, offering money in advance of publication in return for the right to publish the work. In a large number of cases, the books never make enough money to cover the advances. Other examples occur in the initial public offerings of stocks, where prices systematically rise in dramatic fashion in the first day of trading.
The Winner’s Curse and Anchoring and Adjusting
If a bidder fails to take account of the uncertainty in his information or the number of bidders he is bidding against, he might overbid relative to the Nash equilibrium strategy.

|
|
|
|
The Winner’s Curse and Anchoring and Adjusting |
|
111 |
|
Further, when his estimate of the value is high, the expected profit for bidding might become low relative to the Nash equilibrium expected return, or it might even become negative. This phenomenon is called the winner’s curse. Because the highest bidder is the most likely to have overbid the true underlying valuation of the good, if he fails to account for the intricacies of optimal bidding in a Nash equilibrium he is highly likely to lose money for having won the auction.
In describing behavioral theories of why this might happen, two points are important. First, although market prices are the result of the behavior of many market participants, auction prices tend to be the result of just a couple of bidders—and in the case of the firstprice auction one bidder. Thus, in an auction with 100 participants, one irrational bidder who happens to draw a high estimate of the valuation could lead to the behavioral anomaly. Anomalous market prices would require irrational behavior by nearly all participants—an unlikely event. Thus, markets are very stable and robust. Auctions are very volatile, with the outcome depending on each individual participant. Second, the Nash equilibrium under the common-value first-price auction is highly complex. Even in the very simplified version under which I have derived the Nash equilibrium in this chapter, I would guess (from previous experience in teaching) that whereas students understand the concept that bids should be below the estimated valuation, many students of economic theory fail to fully understand how the strategy is derived. I have omitted the derivation of the more complicated general Nash strategy for bidding because it is lengthy enough to be omitted from nearly all game-theory texts, as well as academic papers discussing optimal bidding in the common-value auction. It is then a very strange idea that people who have good training in mathematics and theory have trouble understanding this strategy even when they are concentrating significant cognitive effort on it, yet somehow this same strategy comes naturally to untrained persons who are participating in auctions.
The typical behavioral model of bidding under uncertainty is based on the anchoring and adjustment model. Bidders recognize the error in their estimate and the need to make profit. Thus, they anchor on their estimated value and adjust downward to obtain a bid that is closer to the Nash equilibrium bid. However, because their anchor is high, they fail to adjust downward fully, and thus the bid is too close to the anchor. One result of this model is that the larger the number of bidders, the greater the probability of the winner’s curse. When each participant has an independently drawn estimate of the underlying value, the higher the number of draws, the higher the probability that the highest estimate of value is significantly over the true value. Suppose the estimate of value that is required in order to estimate at or above the true value is v, and the probability of drawing v > v is p. Then the probability that no one draws an estimate greater than v with n bidders is 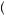 1 − p
1 − p n, which is clearly decreasing as n increases. Thus, we would expect to see many more cases of the winner’s curse with many auction participants rather than with fewer auction participants.
n, which is clearly decreasing as n increases. Thus, we would expect to see many more cases of the winner’s curse with many auction participants rather than with fewer auction participants.
An alternative behavioral model supposes that people underappreciate the impact of information differences between bidders regarding individual bidding behavior. Thus, whereas bidders might correctly anticipate the bids of their competitors, they might not fully attribute the differences in bids to the differences in estimates of the underlying value. Rather they might believe the difference is due to poor strategy on the part of others. This possibility has been implicitly used to explain both the

|
|
|
|
|
112 |
|
THE WINNER’S CURSE AND AUCTION BEHAVIOR |
winner’s curse and several other anomalies in the trade of goods with common yet unknown values.
Most notably, Erik Eyster and Matthew Rabin propose an alternative to the Nash equilibrium in such games. In the Nash equilibrium, people are assumed to know the distribution of estimates of value and to employ the strategy that anticipates the strategies of other players based on this distribution. Alternatively, Eyster and Rabin suppose that people know the true distribution of actions taken by others, but they suppose that these actions have no particular relationship to the underlying estimates of values. Thus, the distribution of actions by others is seen as not representing strategic behavior but just as some static environmental variables. Then the fully cursed equilibrium is given where each player is maximizing the expected payout given the distribution of actions by other players. More generally, the χ -cursed equilibrium assumes that each player assigns probability χ to the event that all other players’ actions are not related to their underlying estimate of valuation (or type), and the remaining 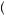 1 − χ
1 − χ probability is assigned to the event that players are fully strategic in responding to their estimate of valuation.
probability is assigned to the event that players are fully strategic in responding to their estimate of valuation.
Let us consider the fully cursed equilibrium of the simple first-price auction considered in the previous section. There are three possible values of the estimate v,  v − 1, v, v + 1
v − 1, v, v + 1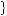 , with a uniform probability distribution, so that p
, with a uniform probability distribution, so that p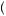 v
v = 1
= 1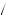 3 for each possible value of v, and n
3 for each possible value of v, and n  2. Suppose again that player 1 draws v1 = 10. As derived previously, the probability distribution of the other player’s estimate of valuation is given by
2. Suppose again that player 1 draws v1 = 10. As derived previously, the probability distribution of the other player’s estimate of valuation is given by
1 |
9 |
if |
v2 = 8 |
|
2 |
9 |
if |
v2 = 9 |
|
p v2 = 1 3 if v2 = 10 |
5 14 |
|||
2 |
9 |
if |
v2 = 11 |
|
1 |
9 |
if |
v2 = 12. |
|
This would result in the probability distribution of the other player’s action z given by
1 |
9 |
if |
z = b 8 |
|
2 |
9 |
if |
z = b 9 |
|
p z = 1 3 if z = b 10 |
5 15 |
|||
2 |
9 |
if |
z = b 11 |
|
1 |
9 |
if |
z = b 12 . |
|
Further, let μ = E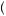 v
v =
= vp
vp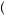 v
v v be the expected value of the item being auctioned given the signal received by the player in question. This expected value in the auctions we have described is just the value of the signal itself. In this case μ = v1 = 10. Given this distribution, player 1 must solve
v be the expected value of the item being auctioned given the signal received by the player in question. This expected value in the auctions we have described is just the value of the signal itself. In this case μ = v1 = 10. Given this distribution, player 1 must solve
max Eχ π = μ − x |
p b v2 = 10 − x |
p b v2 , |
5 16 |
x |
<x |
b v2 <x |
|
b v2 |
|
|
|
|
|
The Winner’s Curse and Anchoring and Adjusting |
|
113 |
|
where Eχ denotes expectation given cursed beliefs, and the probabilities p b
b v2
v2 are drawn from equation 5.15. The key difference between the Nash and the cursed equilibrium is in how the player evaluates the potential payout from a bid. Here, the player multiplies the overall expected benefit should he win the auction, 10 − x, by the probability of winning should he bid, x. However, the player treats winning the auction and the payout he receives as if they are unrelated. He doesn’t recognize that he has a higher probability of winning when he has overbid. When the player does not consider the strategic nature of others’ bids, the relationship between the possible true value and the bids of other players is not considered.
are drawn from equation 5.15. The key difference between the Nash and the cursed equilibrium is in how the player evaluates the potential payout from a bid. Here, the player multiplies the overall expected benefit should he win the auction, 10 − x, by the probability of winning should he bid, x. However, the player treats winning the auction and the payout he receives as if they are unrelated. He doesn’t recognize that he has a higher probability of winning when he has overbid. When the player does not consider the strategic nature of others’ bids, the relationship between the possible true value and the bids of other players is not considered.
Compare this to the equation 5.12, where the player considers the impact of the true underlying valuation on the impact of others’ bids. For example, if the true valuation is low (in this case, 9), the probability of the other player drawing an 8 increases from 0 to 1/3. Equation 5.12 takes this possibility into account when determining the expected payout, whereas the fully cursed equilibrium does not. Here the player only considers the average value given the signal he received and then considers his chances of winning based on that value. The player behaves as if winning the auction is independent of the underlying value.
Recall that the Nash equilibrium strategy was to bid one below the estimated valuation. If player 2 plays b v
v = v − 1, then consider the payout for bidding 9 when your drawn estimate is 10:
= v − 1, then consider the payout for bidding 9 when your drawn estimate is 10:
Eχ π = 1 × |
1 |
+ |
2 |
= |
1 |
. |
5 17 |
|
|
|
|||||
9 |
9 |
3 |
|
|
|||
Alternatively, bidding just slightly more than 9, say 9.1, would yield
Eχ π = |
9 |
× |
1 |
+ |
2 |
+ |
1 |
= 3 , |
5 18 |
|
|
|
|
||||||
10 |
9 |
9 |
3 |
5 |
|
||||
which is much greater than 1/3. Thus, bidding 1 less than your estimated value cannot be the fully cursed equilibrium strategy. In fact, the only strategy that will produce a probability distribution such that the player is not tempted to increase his bid is b v
v = v, yielding Eχ
= v, yielding Eχ 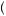 π
π = 0. Further, the true expected payout is found by multiplying the probability of winning given a particular true underlying value by the value of winning in that instance. For simplicity, assume that the bidder in question loses if there is a tie bid. Thus, the probability that the underlying value is 9 is 1/3, and the probability of winning when bidding 10 if the value is 8 is 2/3 (the probability of the other player drawing a 8 or a 9). The value of winning in this case is − 1. The probability that the value is 10 is 1/3, and the probability of winning in this case is 1/3 (the probability the other player draws a 9). The value of winning in this case would be 0. The probability that the true value is 11 is 1/3. The probability of winning in this case is 0. Thus, the true expected profit from winning the auction with a bid of 10 given v = 10 is
= 0. Further, the true expected payout is found by multiplying the probability of winning given a particular true underlying value by the value of winning in that instance. For simplicity, assume that the bidder in question loses if there is a tie bid. Thus, the probability that the underlying value is 9 is 1/3, and the probability of winning when bidding 10 if the value is 8 is 2/3 (the probability of the other player drawing a 8 or a 9). The value of winning in this case is − 1. The probability that the value is 10 is 1/3, and the probability of winning in this case is 1/3 (the probability the other player draws a 9). The value of winning in this case would be 0. The probability that the true value is 11 is 1/3. The probability of winning in this case is 0. Thus, the true expected profit from winning the auction with a bid of 10 given v = 10 is
E π = − 1 × |
1 |
× |
2 |
+ 0 × |
1 |
× |
1 |
+ 0 = − |
2 |
. |
5 19 |
|
|
|
|
|
|||||||
3 |
3 |
3 |
3 |
9 |
|
|
|||||

|
|
|
|
|
114 |
|
THE WINNER’S CURSE AND AUCTION BEHAVIOR |
Thus, the winner would on average lose money. Hence, a rational bidder would never choose to follow this strategy.
More generally, Eyster and Rabin show that in Vickrey auctions with large numbers of bidders, the true expected payout of bidders will be negative, whereas with smaller numbers this might not be the case. They show evidence of such behavior in several experiments involving a wide variety of games with uncertainty. The cursed equilibrium is closely related to the previously mentioned literature on the level of rationality, or degree to which people anticipate the actions of others. In the cursed equilibrium, the player does not believe the others are reacting to his or her private information rather, the player just takes their actions as given.
EXAMPLE 5.7 Experimental Evidence
John Kagel and Dan Levin (and others at the University of Houston) have run several sets of economics experiments to test for the winner’s curse in a well-controlled setting. Subjects were placed in a series of common-value sealed-bid first-price auctions. In each auction, the true value, v, of the item was drawn at random from a uniform distribution on a known interval, 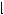 v, v
v, v , that was unknown to the bidders. Each bidder was given a private estimate of the value, v, drawn from a uniform distribution on an interval of known width
, that was unknown to the bidders. Each bidder was given a private estimate of the value, v, drawn from a uniform distribution on an interval of known width 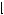 v − ε, v + ε
v − ε, v + ε . The support of the true value ranged from as low as $12 in some auctions to as high as $500 in others. Additionally, they varied the number of bidders in the auctions from as low as three to as many as seven. In all auctions with more than five bidders, the average realized profits were negative, providing substantial evidence of the winner’s curse. In nearly all treatments the winner took away strictly less than the amount implied by Nash-equilibrium bidding. Perhaps more puzzling, the winner was often not the participant given the highest estimate of value. In fact, this phenomenon was more prevalent when there were more bidders. This might suggest that some people respond to the competitiveness of the situation with larger bids in excess of their estimated valuation. Over the course of many rounds of auctions, bidders who had won previous auctions eventually showed some learning and convergence toward the Nash equilibrium behavior.
. The support of the true value ranged from as low as $12 in some auctions to as high as $500 in others. Additionally, they varied the number of bidders in the auctions from as low as three to as many as seven. In all auctions with more than five bidders, the average realized profits were negative, providing substantial evidence of the winner’s curse. In nearly all treatments the winner took away strictly less than the amount implied by Nash-equilibrium bidding. Perhaps more puzzling, the winner was often not the participant given the highest estimate of value. In fact, this phenomenon was more prevalent when there were more bidders. This might suggest that some people respond to the competitiveness of the situation with larger bids in excess of their estimated valuation. Over the course of many rounds of auctions, bidders who had won previous auctions eventually showed some learning and convergence toward the Nash equilibrium behavior.
William Samuelson and Max Bazerman used M.B.A. students to conduct a hypothetical choice experiment describing a mergers and acquisitions problem. With some regularity, it has been shown that when one company decides to purchase another, the purchasing company pays more than the acquired company is worth and receives a negative return on the investment. Many have linked this to the winner’s curse, where the private company might be using their private information and ignoring the publicly available information regarding the company’s value embodied in publicly traded stock prices. For example:
Place yourself in the position of a CEO of a major pharmaceuticals firm who is considering the purchase of a smaller firm in the same field. Should you decide to acquire the smaller firm, your firm will pay cash and purchase all of the firms outstanding stock. The smaller firm is heavily invested in a project that could produce a cure for common form of cancer. In the best case

|
|
|
|
The Winner’s Curse and Anchoring and Adjusting |
|
115 |
|
scenario, if the project pays off, the company will be worth $100/share. If the project does not yield such a cure, the company could be worth as little as $0/ share. You consider all share values between $0 and $100 to be equally likely to occur. Because the companies perform similar tasks, there are some potential cost savings should you decide to acquire the smaller firm. Thus, the smaller firm is worth approximately 1.5 times as much to your firm as it would be worth on the market generally. The smaller firm already knows whether their project will pay off or not, and will only accept an offer that exceeds the anticipated fair price per share of their firm. What would you bid?
The correct answer to this question would consider the amount of value obtained if the bid is accepted. Samuelson and Bazerman conducted an experiment asking participants to make a similar decision. If any bid of $x per share is accepted, then the fair value can be at most $x per share, otherwise this bid would be rejected. With a uniform distribution of possible values between $0 and $x per share, the expected value per share given the bid is accepted is E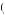 x
x = $x
= $x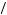 2. In this case, the expected value of purchasing the smaller firm per share is $1.5E
2. In this case, the expected value of purchasing the smaller firm per share is $1.5E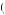 x
x − $x = $3x
− $x = $3x 4 − $x = − $x
4 − $x = − $x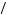 4. Thus, if the firm is willing to accept your bid, you do not want the company. The optimal bid is zero. However, if, as in the cursed equilibrium, the bidder does not consider the strategic action of the firm but only the expected gain, then the bidder will use the expected value of the smaller firm, not conditioned on whether the bid is accepted, to calculate the potential gain. This expected value is $50 per share. The expected benefit of acquiring the smaller firm would be 1.5 times this expected value, $75, and thus the bidder would choose some value between $50 and $75.
4. Thus, if the firm is willing to accept your bid, you do not want the company. The optimal bid is zero. However, if, as in the cursed equilibrium, the bidder does not consider the strategic action of the firm but only the expected gain, then the bidder will use the expected value of the smaller firm, not conditioned on whether the bid is accepted, to calculate the potential gain. This expected value is $50 per share. The expected benefit of acquiring the smaller firm would be 1.5 times this expected value, $75, and thus the bidder would choose some value between $50 and $75.
Samuelson and Bazerman’s experiment provided monetary incentives to some participants by paying them a fraction of the value of the acquisition. In fact, bidders who were given monetary incentives, as well as those who were not, all bid positive amounts for the firm, contrary to the optimal strategy. In both cases, more than half of the bids fell between $50 and $75, demonstrating something that closely resembles cursed equilibrium behavior.
EXAMPLE 5.8 Building Contractors
Construction firms are often required to bid on larger projects that could be worth substantial amounts in terms of revenue and profits. However, in this case, the firm bids their payment for construction, and then they must construct the building project for some unknown cost. The uncertainties involved in construction projects lead costs to be substantially volatile. Given this need to participate in regular auctions, one might expect construction firms to face the winner’s curse, leading to eroding profits and potential failure. In laboratory experiments, building contractors, in fact, fall prey to the winner’s curse. But there is much less evidence of the winner’s curse in real-life construction bidding. Douglas Dyer and John Kagel used interviews with building contractors as well as some publicly available bidding data to learn why there might be a difference
