
- •Brief Contents
- •Contents
- •Preface
- •Who Should Use this Book
- •Philosophy
- •A Short Word on Experiments
- •Acknowledgments
- •Rational Choice Theory and Rational Modeling
- •Rationality and Demand Curves
- •Bounded Rationality and Model Types
- •References
- •Rational Choice with Fixed and Marginal Costs
- •Fixed versus Sunk Costs
- •The Sunk Cost Fallacy
- •Theory and Reactions to Sunk Cost
- •History and Notes
- •Rational Explanations for the Sunk Cost Fallacy
- •Transaction Utility and Flat-Rate Bias
- •Procedural Explanations for Flat-Rate Bias
- •Rational Explanations for Flat-Rate Bias
- •History and Notes
- •Theory and Reference-Dependent Preferences
- •Rational Choice with Income from Varying Sources
- •The Theory of Mental Accounting
- •Budgeting and Consumption Bundles
- •Accounts, Integrating, or Segregating
- •Payment Decoupling, Prepurchase, and Credit Card Purchases
- •Investments and Opening and Closing Accounts
- •Reference Points and Indifference Curves
- •Rational Choice, Temptation and Gifts versus Cash
- •Budgets, Accounts, Temptation, and Gifts
- •Rational Choice over Time
- •References
- •Rational Choice and Default Options
- •Rational Explanations of the Status Quo Bias
- •History and Notes
- •Reference Points, Indifference Curves, and the Consumer Problem
- •An Evolutionary Explanation for Loss Aversion
- •Rational Choice and Getting and Giving Up Goods
- •Loss Aversion and the Endowment Effect
- •Rational Explanations for the Endowment Effect
- •History and Notes
- •Thought Questions
- •Rational Bidding in Auctions
- •Procedural Explanations for Overbidding
- •Levels of Rationality
- •Bidding Heuristics and Transparency
- •Rational Bidding under Dutch and First-Price Auctions
- •History and Notes
- •Rational Prices in English, Dutch, and First-Price Auctions
- •Auction with Uncertainty
- •Rational Bidding under Uncertainty
- •History and Notes
- •References
- •Multiple Rational Choice with Certainty and Uncertainty
- •The Portfolio Problem
- •Narrow versus Broad Bracketing
- •Bracketing the Portfolio Problem
- •More than the Sum of Its Parts
- •The Utility Function and Risk Aversion
- •Bracketing and Variety
- •Rational Bracketing for Variety
- •Changing Preferences, Adding Up, and Choice Bracketing
- •Addiction and Melioration
- •Narrow Bracketing and Motivation
- •Behavioral Bracketing
- •History and Notes
- •Rational Explanations for Bracketing Behavior
- •Statistical Inference and Information
- •Calibration Exercises
- •Representativeness
- •Conjunction Bias
- •The Law of Small Numbers
- •Conservatism versus Representativeness
- •Availability Heuristic
- •Bias, Bigotry, and Availability
- •History and Notes
- •References
- •Rational Information Search
- •Risk Aversion and Production
- •Self-Serving Bias
- •Is Bad Information Bad?
- •History and Notes
- •Thought Questions
- •Rational Decision under Risk
- •Independence and Rational Decision under Risk
- •Allowing Violations of Independence
- •The Shape of Indifference Curves
- •Evidence on the Shape of Probability Weights
- •Probability Weights without Preferences for the Inferior
- •History and Notes
- •Thought Questions
- •Risk Aversion, Risk Loving, and Loss Aversion
- •Prospect Theory
- •Prospect Theory and Indifference Curves
- •Does Prospect Theory Solve the Whole Problem?
- •Prospect Theory and Risk Aversion in Small Gambles
- •History and Notes
- •References
- •The Standard Models of Intertemporal Choice
- •Making Decisions for Our Future Self
- •Projection Bias and Addiction
- •The Role of Emotions and Visceral Factors in Choice
- •Modeling the Hot–Cold Empathy Gap
- •Hindsight Bias and the Curse of Knowledge
- •History and Notes
- •Thought Questions
- •The Fully Additive Model
- •Discounting in Continuous Time
- •Why Would Discounting Be Stable?
- •Naïve Hyperbolic Discounting
- •Naïve Quasi-Hyperbolic Discounting
- •The Common Difference Effect
- •The Absolute Magnitude Effect
- •History and Notes
- •References
- •Rationality and the Possibility of Committing
- •Commitment under Time Inconsistency
- •Choosing When to Do It
- •Of Sophisticates and Naïfs
- •Uncommitting
- •History and Notes
- •Thought Questions
- •Rationality and Altruism
- •Public Goods Provision and Altruistic Behavior
- •History and Notes
- •Thought Questions
- •Inequity Aversion
- •Holding Firms Accountable in a Competitive Marketplace
- •Fairness
- •Kindness Functions
- •Psychological Games
- •History and Notes
- •References
- •Of Trust and Trustworthiness
- •Trust in the Marketplace
- •Trust and Distrust
- •Reciprocity
- •History and Notes
- •References
- •Glossary
- •Index

|
|
|
|
|
234 |
|
DECISION UNDER RISK AND UNCERTAINTY |
FIGURE 9.4
The Common Ratio
Effect in the
Marschak–Machina
Triangle
p(4,000) = 1 |
|
|
|
|
|
B |
|
Probability of $4,000 |
|
|
|
|
|
|
D |
p(4,000) = 0 |
A |
|
C |
p(0) = 0 |
Probability of $0 |
p(0) = 1 |
|
As with the common outcome effect, the common ratio effect is a violation of the independence axiom. This can be seen in Figure 9.4. The gambles A and B in the triangle form a line segment with the same slope as the line segment connecting C and D. Thus any indifference curve that places A to the northwest and B to the southeast would imply indifference curves that place C to the northwest and D to the southeast. Instead, the observed choice suggests that indifference curves are steeper in the western portion of the triangle than they are in the southeastern corner. As with the common outcome effect, probability weighting and regret provide two competing explanations for the violation of expected utility.
Allowing Violations of Independence
Both the common ratio and common consequence effects suggest that indifference curves are steeper in the western portion of the Marschak–Machina triangle than in the southeast portion. This led some to suppose that instead of parallel indifference curves, indifference curves fan out across the Marschak–Machina triangle. One way to salvage the axioms, or behavioral rules, that serve as the foundations for expected utility is to replace the independence axiom with the betweenness axiom.
Betweenness Axiom
If A 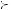 B, and C is a compound gamble that yields A with probability p and B with probability
B, and C is a compound gamble that yields A with probability p and B with probability 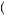 1 − p
1 − p , then betweenness is satisfied if A
, then betweenness is satisfied if A 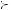 C
C 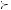 B.
B.
|
|
|
|
Allowing Violations of Independence |
|
235 |
|
p(100) = 1 Eu(x) = u(100)
Probability of $100
Eu(x) = u(50)
p(100) = 0 |
|
Eu(x) = u(0) |
FIGURE 9.5 |
|
|
|
|
||
p(0) = 0 |
Probability of $0 |
p(0) = 1 |
Indifference Curves under Betweenness |
|
The betweenness axiom allows indifference curves to have different slopes, but it still requires indifference curves to be straight lines. Thus, the indifference curves may be like those displayed in Figure 9.5. To see that indifference curves must be straight lines, consider the gambles A and B that lie on a single indifference curve. Any gamble located directly between points A and B represents a gamble that is a combination of A and B (called C in the definition). Thus, betweenness requires that the gambler be indifferent between A, B, and C, and thus C must also lie on the indifference curve.
One of the first proposed theories to employ betweenness is called weighted expected utility theory. Let p1, .. , pn be the probabilities associated with outcomes x1, 

 , xn. Then weighted expected utility preferences suppose that people act to maximize their weighted utility, which is given by
, xn. Then weighted expected utility preferences suppose that people act to maximize their weighted utility, which is given by
|
n |
|
|
U = |
i = 1 piu xi |
. |
9 31 |
n |
|||
|
i = 1 piv xi |
|
|
Here, u x
x is a standard utility of wealth function, and v
is a standard utility of wealth function, and v x
x constitutes some function used to weight the probabilities associated with particular outcomes. To derive indifference curves, consider all points
constitutes some function used to weight the probabilities associated with particular outcomes. To derive indifference curves, consider all points  p1, p2
p1, p2 such that
such that
p1u x1 + p2u x2 + 1 − p1 − p2 u x3 |
= k, |
9 32 |
|
||
p1v x1 + p2v x2 + 1 − p1 − p2 v x3 |
|
|
where the left side of equation 9.32 corresponds to the definition of weighted utility from equation 9.31, and the right side is just a constant. Rearranging obtains
p1 u x1 − u x3 − k v x1 − v x3 + p2 u x2 − u x3 − k v x2 − v x3
9 33
33
+ u x3 − kv x3 = 0,
|
|
|
|
|
236 |
|
DECISION UNDER RISK AND UNCERTAINTY |
which, because outcomes and the functions u and v are fixed, yields an equation of the standard linear format p1c1 + p2c2 + c3 = 0. To see that the slopes of the indifference curves may be different, note that k is a parameter of the constants c1, c2 and c3. Thus, the slope depends upon the level of utility indicated by the indifference curve.
Several have noted that the weighted utility model does fit the data in the triangle significantly better than the expected utility model. However, others have noted that there is significant evidence that betweenness is violated. Colin Camerer and Tek-Hua Ho find that in laboratory settings, people show clear evidence of nonlinear indifference curves. Interestingly, however, the shape of the indifference curves depends substantially on the types of gambles presented. In particular, gambles that involve losses generate a very different pattern of indifference curves from those generated by gambles involving gains.
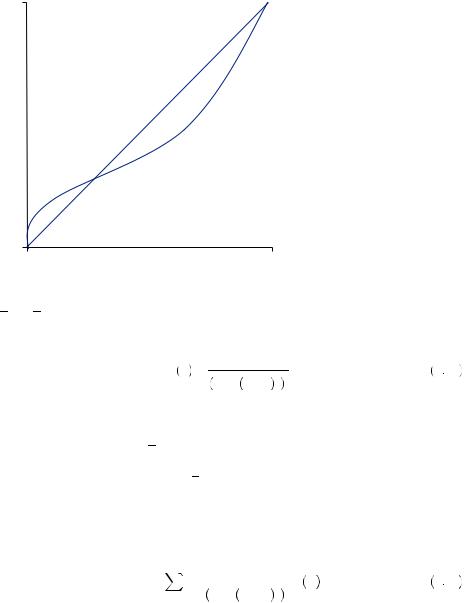
The Shape of Indifference Curves
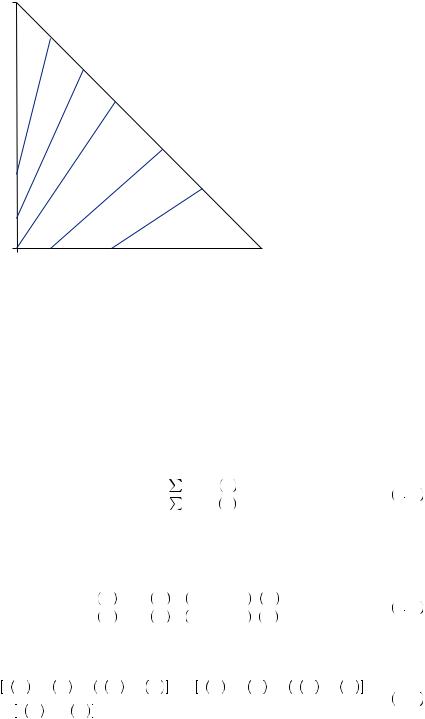
By repeatedly asking people to choose between pairs of gambles representing different points in the Marschak–Machina triangle, experimental economists have discovered many regularities in the shapes of these indifference curves. Figure 9.6 provides an example of the general shapes of indifference curves found in laboratory experiments for gambles involving gains. In general, the curves are steeper than the 45-degree line in the northwest portion of the triangle, and they are flatter than the 45-degree line in the southeast portion of the triangle. The curves display significant fanning out around both the vertical and horizontal axes. However, the curves are close to parallel in the center of the triangle. There is some weak evidence that curves actually fan in around the hypotenuse of the triangle. Thus, the places where violations of expected utility are most likely to occur are near the edges of the triangle, where very large and very small probabilities are involved. Interestingly, when gambles with losses are examined, the indifference curves appear to be
|
Probability of highest value |
FIGURE 9.6 |
|
Indifference Curves in |
|
the Triangle for Gam- |
|
bles Involving Gains |
Probability of lowest value |

|
|
|
|
Evidence on the Shape of Probability Weights |
|
237 |
|
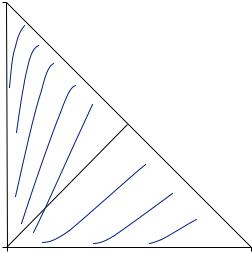
Probability of highest value
|
|
FIGURE 9.7 |
Probability of lowest value |
|
Indifference Curves in the Triangle for Gambles |
|
||
|
Involving Losses |
reflected around the 45-degree line (see Figure 9.7). This reflection results in many of the same properties but some distinct differences. In particular, people appear to be more risk loving (more shallow curves) in the center of the triangle.
Evidence on the Shape of Probability Weights
Malcolm G. Preston and Philip Baratta were the first to experiment with using probability weights to describe deviations from expected utility theory. They conducted several experiments in which they auctioned off various simple gambles (with some probability of winning an outcome and remaining probability of winning nothing). They discovered that willingness to pay for gambles was approximately linear in the amount of the reward but highly nonlinear in the probability associated with the outcome. This led them to suppose that people were misperceiving the probabilities in very systematic ways. In particular, people appeared to overweight small probabilities and underweight large probabilities. Similar work has confirmed their early findings with respect to the general shape of these perceived probabilities. Such systematic misperceptions would explain some of the violations of expected utility such as the common ratio and common consequence effects.
One prominent theory of decision under risk supposes that people seek to maximize their perceived expected utility, where their perception is described by probability weights (discussed earlier in examples 9.3 and 9.4). Probability weights are given by a function π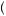 p
p , which maps probabilities onto the unit interval. Generally π
, which maps probabilities onto the unit interval. Generally π p
p is thought to be an increasing function of the true probability, with π
is thought to be an increasing function of the true probability, with π p
p > p for all p < p and π
> p for all p < p and π p
p < p for p > p. Moreover, experimental evidence suggests that π
< p for p > p. Moreover, experimental evidence suggests that π

 is a concave function when p < p, and a convex function when p > p. A typical probability weighting function is depicted in Figure 9.8. Generally, the fixed point (the point p such that
is a concave function when p < p, and a convex function when p > p. A typical probability weighting function is depicted in Figure 9.8. Generally, the fixed point (the point p such that
|
|
|
|
|
238 |
|
DECISION UNDER RISK AND UNCERTAINTY |
1
Probability weight
FIGURE 9.8 |
0 |
|
|
A Typical Probability |
|
1 |
|
Weighting Function |
0 |
Probability p |
|
|
|
p = π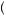 p
p ) is believed to be smaller than 0.5. One commonly used functional form for a probability weighting function is given by
) is believed to be smaller than 0.5. One commonly used functional form for a probability weighting function is given by
π p = |
pγ |
|
pγ + 1 − p γ 1γ . |
9 34 |
This function has the same inverted s-shape as the function presented in Figure 9.8. Probability weights imply subadditivity under the right circumstances (for example, if all probabilities are larger than p) and could thus explain the certainty effect. Alternatively, probability weighting would imply superadditivity (probabilities sum to greater than 1) if all outcomes had probability below p, suggesting uncertain outcomes would be unduly preferred to certain outcomes in some cases.
Finally, probability weighting functions make preferences a nonlinear function of the probabilities. For example, using the probability weighting function above, the value of a gamble would be given by
V = |
n |
|
piγ |
|
U xi . |
9 35 |
i = 1 |
γ |
|
1 |
|||
|
1 − pi |
γ |
|
|||
|
|
pi + |
γ |
|
||
|
|
|
|
|
||
Given the highly nonlinear nature of the function with respect to the probabilities, the indifference curves are also necessarily very nonlinear, potentially allowing the possibility of explaining some of the fanning out or fanning in of the indifference curves. In particular, if the slope of the probability weighting function only changes substantially for very high probabilities or very low probabilities, that might explain why the indifference curves in the triangle only display changes in slope near the edges of the triangle (or where some probability is necessarily low and another is necessarily high).
