2 Уровень

4. Выберите ответ из числа предложенных, укажите в ответе соответствующую букву.

– Прямые с и d принадлежат плоскости β. Могут ли прямые с и d быть параллельными?

а) да; б) нет.

– Прямые а и в параллельны. Прямая с пересекает прямую а, но не пересекает в. Как расположены прямые с и в?

а) параллельны; б) пересекаются; в) скрещиваются.

– Прямая а пересекает плоскость α. Может ли в плоскости α лежать прямая, параллельная а?

а) да; б) нет.

5. Ответьте на вопросы и сделайте соответствующие пояснения (рисунки):

– Сколько случаев взаимного расположения прямой и плоскости в пространстве?

– Сколько можно провести через данную точку прямых, параллельных данной плоскости?

– Сколько можно провести через данную точку плоскостей, параллельных данной прямой?

3 Уровень

6. Известно, что прямая параллельна плоскости.

а) Параллельна ли она любой прямой в этой плоскости? Ответ поясните.

б) Может ли данная прямая пересечь хотя бы одну из прямых этой плоскости? Ответ обоснуйте.

в) Какие могут быть случаи расположения данной прямой с другими прямыми этой плоскости?

7. Как могут быть расположены прямая а и плоскость α, если данная прямая и некоторая прямая, лежащая в плоскости α, скрещиваются? Сделайте рисунок и поясните ответ соответствующими записями.

8. Верны ли утверждения?

– Если прямая а параллельна плоскости α и прямая b параллельна прямой а, то прямая b параллельна плоскости α. (Рассуждайте методом от противного). Сделайте рисунок.

– Если прямые а и b параллельны плоскости α, то и прямая b параллельна прямой а. (Ответ обоснуйте, приведите контрпример и сделайте соответствующие пояснения и рисунок).

Задание 4

Математические задачи для классов различного профиля и их решение

Замечание 1. Примеры математических задач для классов различного профиля приведены при выполнении общего задания 2.

Замечание 2. Примеры решения задач приведены при выполнении общего задания 3.

Задание 5

Методика обучения решению тригонометрических уравнений

Методика обучения решению тригонометрических уравнений включает следующие ключевые вопросы:

1) изучение решения тригонометрических уравнений:

а) простейшего вида sinx= a, cosx= a, tqx= a, ctqx = a;

б) уравнений, которые после введения новой переменной приводятся к квадратным;

в) однородных тригонометрических уравнений (1-го и 2-го порядков);

г) уравнений, для решения которых надо разложить на множители левую часть, приравняв затем каждый множитель к нулю.

2) подбор учебных задач, на формирование умений приводить тригонометрические уравнения к простейшему виду, к одинаков углам, к одинаковым функциям, к однородным уравнениям.

3) анализ, вывод и обобщение общего приема решения тригонометрических уравнений.

Примеры учебных задач, на усвоение общего приема решения

тригонометрических уравнений

1. Приведите примеры тригонометрических уравнений.

2. Придумайте тригонометрические уравнения, функции в которых имеют одинаковые углы.

3. Из предложенных уравнений выберите те, в которых тригонометрические функции имеют одинаковые углы:

а) sin²2x + cosx + c = 0; б) sin²+ cosy + b = 0; в) sin² α + cos α + c = 5.

4. Приведите тригонометрические функции, входящие в уравнения, к одинаковым углам: а) 3cos2x + sin²x + 5 sinx cosx = 0; б) 3 + sin 2x = 4sin²x; в) 2 + cos²x = cos .

5. Сделайте замену в данных тригонометрических уравнениях:

а) 2 ctg²x – 5 ctgx – 3 = 0; б) tg²x – 5 tgx – 7 = 0.

Общий прием решения тригонометрических уравнений можно представить в виде блок-схемы.

Б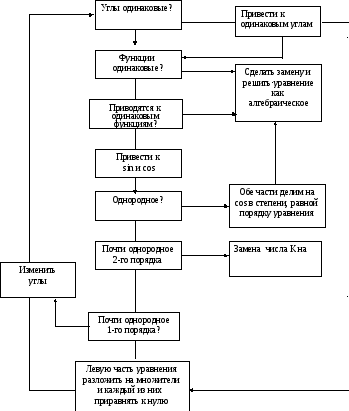лок-схема решения тригонометрических уравнений

Рис. 4

6. Из предложенных уравнений выберите однородное:

а) 5cosx + 3 sinx = 0; б) 3cosxsinx + 2 cosx = 0;

в) 2 sin² x + cosx sinx + 3 cos²x = 0;

г) 3 cos²x + 2 sinx – 4 sin²x = 5 cosx.

7. Придумайте тригонометрические уравнения, которые были бы однородными.

8. Из предложенных уравнений выберите почти однородные тригонометрические уравнения:

а) 3cosx + 2 sinx = 5; б) cos²x + 2 cosx sinx = 1; в) 3sin²x – 5 sinx cosx = – 2 cos²x.

9. Разложите левую часть тригонометрического уравнения на множители:

а) 2sin cos – 2cos²; б) cos 3x – 1 = cos 2x; в) sin 3x cos 3x = sin 5x.