Общий прием решения математической задачи

1) Изучите содержание задачи (выделите данные и искомые, сделайте чертеж, схему и т. п.).

2) Если нужно, проведите анализ – поиск решения (вспомните: есть ли специальный прием анализа или решения задач данного типа, известны ли похожие задачи, провести общий анализ задачи и т. п.).

3) На основе анализа составьте план решения или сформулируйте известный план решения задач данного типа (при этом следите, все ли данные задачи использованы, нельзя ли преобразовать искомые или данные задачи для более быстрого составления плана).

4) Решите задачу по составленному плану (при реализации плана проверьте правильность каждого шага, правильно замените термины и символы их определениями, используйте свойства данных в задаче объектов).

5) Запишите решение, используя приемы записи.

6) Если нужно, проверьте или исследуйте решение (используйте способы проверки: проверьте ход решения, проверьте результат, решите задачу другим способом, используйте специальные приемы проверки решения задач данного типа).

7) Рассмотрите другие возможные способы решения, выберите рациональный.

8) Запишите ответ.

9) Проанализируйте информацию, полученную в процессе решения задачи, выделите главное, обобщите, включите в систему прежнего знания о приемах работы над задачей.

Арифметические задачи

Основные типы арифметических задач: «выполнить действия», «вычислить значения числового выражения», «решить текстовую задачу (задачи-расчеты, текстовые задачи с сюжетом)». Наиболее трудными из них являются текстовые задачи.

Прием поиска решения текстовой арифметической задачи (с сюжетом)

1) Изучите содержание задачи.

2) Определите, исходя из задачной ситуации, тип задачи: а) на прямое выполнение какого-либо действия, б) «на движение», в) «на пропорции», г) на проценты, д) «на кратное отношение искомых величин», е) «на совместную работу», ж) «на среднее арифметическое», з) «на смеси», и) «на натуральные числа» - и вспомните известный прием ее решения.

3) Если п.2 не дал результата, проведите общий (восходящий или нисходящий) анализ, приводящий к плану решения.

4) Если п.3 не дал результата, вспомните задачу, аналогичную данной, прием решения которой известен, сравните их, и на этой основе составьте план решения.

5) Если п.4 не дал результата, временно измените условие или требование задачи так, чтобы можно было сравнить полученную задачу с данной; затем использовать отмеченный в п.4 прием аналогии.

Прием решения текстовой арифметической задачи

1) Изучите содержание задачи, используя приемы (краткую запись, схему, таблицу, геометрическую иллюстрацию).

2) Проведите анализ – поиск решения, используя прием поиска.

3) На основе анализа или известного приема решения составьте план решения данной задачи.

4) Решите задачу по составленному плану.

5) Запишите решение с использованием соответствующей символики.

6) Если нужно, проверьте или исследуйте решение.

7) Рассмотрите другие возможные способы решения, выберите наиболее рациональный.

8) Запишите решение и ответ, используя приемы записи.

Методика обучения учащихся решению арифметической задачи

В качестве примера рассмотрим следующую задачу (5 класс): «Велосипедист ехал 3 часа со скоростью 18 км/ч. Обратно он ехал другой дорогой, которая была короче на 9 км, но ехал со скоростью на 3 км/ч меньшей. Сколько времени велосипедист затратил на обратную дорогу?»

1. Подготовительный этап. Изучить содержания задачи - установить зависимости между расстоянием, скоростью и временем; может быть представлено в системе устных упражнений через выполнение заданий на повторение этих зависимостей. Например, задача: «Пешеход идет в течение 3-х часов со скоростью 5 км/ч.» Что можно определить? (расстояние) Как? (можно определить расстояние: ()км). Записать зависимость формулой (S = v t, =15).

2. Чтение задачи. Записать содержание задачи (если в задаче встречаются незнакомые термины, выяснить их смысл). Содержание задачи может быть записано по-разному. Например, с помощью таблицы или схемы (рис.3):

Таблица 12

	Скорость	Время	Расстояние
1 путь	18 км/ч	3 ч	?
2 путь (обратный)	На 3 км/ч медленнее	?	на 9 км короче

Скорость на пути АВ – 18км/ч;

Время движения на АВ – 3 ч;

Расстояние АВ - ?

Скорость на пути ВА (?) – на 3 км/ч меньше, чем скорость

Расстояние ВА - ? – на 9 км меньше, чем

Время движения на ВА - ?

Рис. 3. Изучение содержания задачи (схема)

3. Анализ содержания и составление плана решения задачи. Анализ содержания задачи (поиск решения) может быть представлен:

а) в виде схемы (рис. 4)

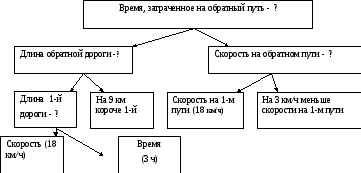
Рис.4. Анализ содержания задачи (схема)

б) системы вопросов:

1) Какой главный вопрос задачи? (Сколько времени велосипедист затратил на обратную дорогу?)

2) Можно ли сразу на него ответить? (Нет, т. к. неизвестны обратный путь и скорость велосипедиста на обратном пути).

3) Нельзя ли определить скорость велосипедиста на обратном пути? (Можно, т. к. известна скорость велосипедиста на 1-м пути, и известно, насколько она отличается от скорости на отрезке пути).

4) Нельзя ли определить длину обратного пути? (Сразу нет, но можно сначала найти длину первого пути, т. к. известна скорость и время, а затем и длину 2-го пути).

План решения задачи:

Найти последовательно:

1) длину 1-го пути;

2) длину 2-го пути;

3) скорость на 2 участке пути;

4) время, затраченное на обратную дорогу;

4. Выполняем план решения задачи (рис.5).

Синтез решения задачи:

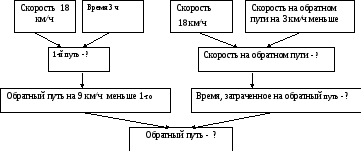
Рис.5. Синтез решения задачи (схема)

Способы записи решения задачи

1-й способ

Запись решения числовой формулой

1. На 1-м пути велосипедист проехал: 18 * 3 км.

2. На обратном пути велосипедист проехал: (18 * 3 – 9) км.

3. Скорость велосипедиста на обратном пути: (18 – 3) км/ч.

4. На обратный путь велосипедист затратил: (18 * 3 – 9) : (18 – 3) ч.

Находим числовое значение выражения (устно).

Ответ: на обратный путь велосипедист затратил 3 часа.

2-й способ

Вопросно-ответная форма

1. Какова длина первой дороги? 18 * 3 = 54 (км)

2. Какова длина второй дороги? 54 – 9 = 45 (км)

3. Какова скорость велосипедиста на обратном пути? 18 – 3 = 15 (км/ч)

4. Сколько времени затрачено на обратную дорогу? 45 : 15 = 3 (ч)

Ответ: 3 часа.

3-й способ

Запись только действий

1. 18 * 3 = 54 (км).

2. 54 – 9 = 45 (км).

3. 18 – 3 = 15 (км/ч).

4. 45 : 15 = 3 (ч).

Ответ: 3 часа.

4-й способ

Запись решения с пояснением

1. 18 * 3 = 54 (км) – длина 1-го пути.

2. 54 – 9 = 45 (км) – длина 2-го пути.

3. 18 – 3 = 15 (км/ч) – скорость велосипедиста на 2 участке пути.

4. 45 : 15 = 3 (ч) – затратил велосипедист на обратный путь.

Ответ. 3 часа.

Дополнительная работа над задачей после ее решения

1. Запись решения задачи в виде числовой формулы, если запись была иной.

2. Составление задачи, аналогичной решенной.

3. Составление одной из обратных задач и другие способы.

4. Выявление и обобщение действий по решению задачи.

Замечание: Формулировка той же задачи может быть дана иначе. Например: «Коля и Петя ехали из города разными дорогами в лагерь. Коля ехал по дороге, которая была короче на 9 км, но ехал со скоростью на 3 км/ч меньшей, чем Петя. А Петя ехал 3 часа со скоростью 18 км/ч». Поставьте вопрос и решите задачу (Кто из мальчиков раньше приедет в лагерь?).