III уровень

Комбинации пространственных тел. Вписанные и описанные шары

При решении задач на комбинацию геометрических фигур ввиду сложности выполнения чертежей часто приходится прибегать к их упрощению. В одних случаях оказывается достаточным иметь лишь изображение сечения фигур, участвующих в комбинации (таково большинство задач на комбинацию круглых тел), в других – изображение лишь одной из комбинируемых фигур; иногда одну из фигур бывает необходимо изобразить полностью, а другую лишь частично.

В данной теме решаются, в основном задачи на вычисление; методы решения: арифметический, алгебраический.

Решить математическую задачу, используя общий прием решения

III уровень

Задача. Найти область определения функции, заданной формулой:

lg(х² - 9).

1. Изучить содержание задачи. Данная функция задана формулой, представляющей сумму двух выражений: иррационального и логарифмического. Подкоренное выражение представлено алгебраической дробью, содержащую переменную в знаменателе.

2) Поиск решения. Область определения функции можно найти как пересечение области определения первого и второго выражений. В область определения этой функции входят те значения х, при которых знаменатель подкоренного выражения и выражение под знаком логарифма положительны.

3) Решение задачи. Составим и решим систему неравенств:

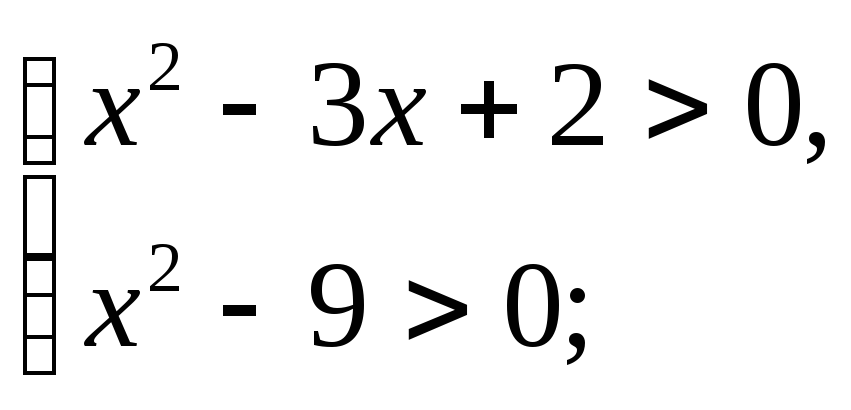или

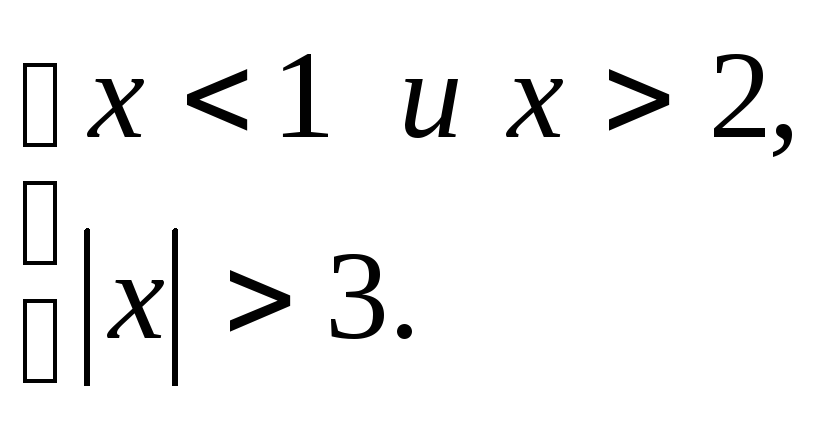
4) Ответ: (-; -3) (3; +).

5) Анализ и обобщение решения задачи. Задача решена на основе общего приема нахождения области определения функции и приема решения системы неравенств.

Задание 4

Типичные ошибки учащихся при изучении стереометрии

1) Ошибки при выполнении стереометрического чертежа: при изображении углов между прямыми и плоскостями, между плоскостями, при изображении многогранников, особенно высоты пирамиды или наклонной призмы, центров сферы и шара и т.п.

2) Логические ошибки: при определении понятий, ошибки в доказательствах, в выводах формул.

3) Ошибки при решении задач: путают свойства прямого и прямоугольного параллелепипеда, неправильно указывают диагональные сечения и т.п.

Коррекция:

Эффективным средством профилактики затруднений учащихся при решении задач, в частности, построения чертежа, являются специальные учебные (подготовительные) задачи.

Задача: В основании призмы АВСА₁В₁С₁ лежит правильный треугольник. Ее вершина А₁ одинаково удалена от вершин А, В, С, а ее высота равна стороне основания. Считая сторону основания равной а, найдем S _бок. – площадь боковой поверхности призмы.

Учебные задачи:

1) Изобразить призму, в основании которой лежит правильный треугольник;

2) Является ли данная призма правильной? Почему?

3) Какое условие необходимо, чтобы призма была правильной; сформулируйте определение правильной треугольной призмы;

4) Дан правильный треугольник. Постройте какую-либо точку, одинаково удаленную от вершин этого треугольника а) на плоскости; б) в пространстве.

Примеры выполнения индивидуальных учебных заданий Задание 1

Таблица 13

Тематический план для образовательных классов (фрагмент)

Тема «Многогранники» (18 ч.)