Многоканальная смо с отказами

Впервые такая модель была исследована датским математиком А. К. Эрлангом в связи с развитием телефонных систем.

В 1909г., а затем в 1917г., А. К. Эрланг опубликовал важные результаты по оценке характеристик этих систем в установившемся режиме.

Г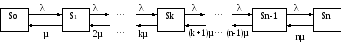раф состоянийn- канальной СМО с отказами представлен на рис.10.40.

Рис. 10.40.Граф состояний многоканальной СМО с отказами

СМО может находится в одном их следующих n+1 состояний:

S₀– всеnканалы свободны;

S1– занят только один канал;

…

S_k– занятыkканалов;

…

S_n– заняты всеnканалов.

Переходы слева направо, из низших состояний (k) в высшие (k+1), происходят с одной и той же плотностью потока λ. В обратном направлении плотность потока уменьшается отnµ (могут освободиться сразуnканалов) до µ (может освободиться один канал).

Составим в соответствии с правилом А. Н. Колмогорова систему линейных алгебраических уравнений относительно вероятностей состояний.

На графе состояний системы указано, что переход из состояния S1вS₀происходит с интенсивностью µ, а изS2вS1– с интенсивностью 2µ .

Это объясняется тем, что состояние S2– это состояние системы, в котором заняты (работают) два канала.

Освобождение каждого из них происходит с интенсивностью µ, поэтому освобождение либо одного из них (первого), либо другого (второго) происходит с суммарной интенсивностью 2µ.

Для многоканальной СМО с отказами имеем следующие интенсивности переходов:

λ₀= λ1=…=λ_k-1=…= λ_n-1= λ ;

µ₀=µ;

µ₁=2µ;

---------

µ_k-1=kµ;

---------

µ_n-1=nµ.

При этих интенсивностях в соответствии с формулами решения уравнений для схемы ''гибели и рождения'' получаем следующие соотношения для α_k, определенные через ρ

α₀ =1

;

-----------------------------------------

;

-----------------------------------------

.

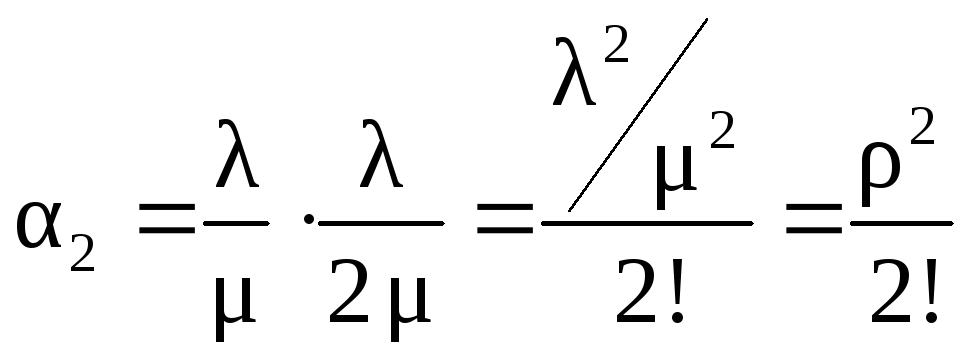Вероятности состояний с учетом того, что α₀=1 записываются в виде:

;

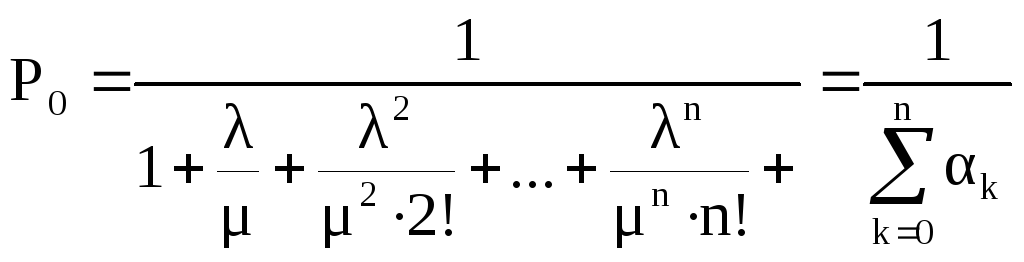P_k = α_k  P₀;

P_n = α_n  P₀.

Подставив в выражение для вероятностей состояния соотношение, определяющее α_kчерез ρ, и учитывая, чтополучаем формулы Эрланга.

;

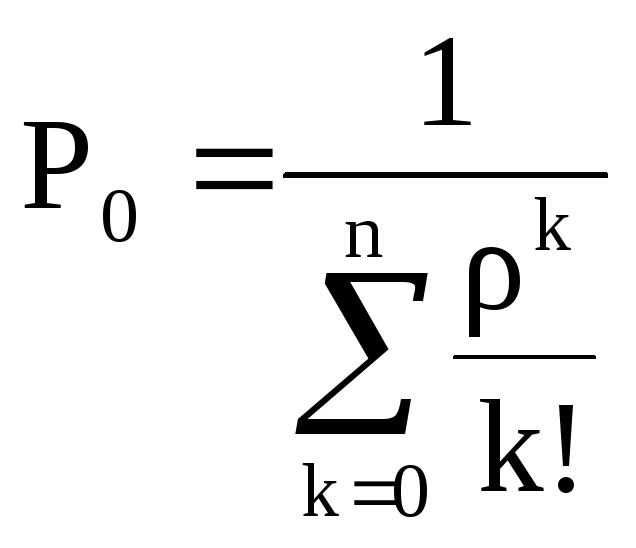, k=1,n;

.

Задача.

Задана СМО с n=2 и=1.

Решение:

.

.

.

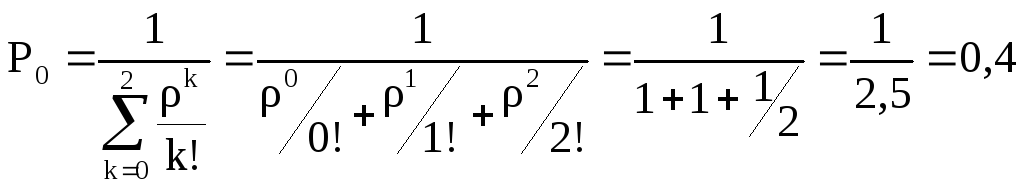10.7. Имитационное моделирование систем массового обслуживания Метод статистических испытаний (метод Монте-Карло)

Имитационное моделирование основывается на экспериментах с моделью реальной системы. Если реальная система находится под воздействием случайных факторов или имеет случайные характеристики, что для определения характеристик системы требуется выполнить статистические испытания.

Статистические испытания предполагают многократное повторение однотипных экспериментов. Каждый эксперимент осуществляется при определенном наборе случайных чисел.

Совокупность большого числа подобных испытаний обнаруживает статистическую устойчивость и может быть использована для количественной оценки системы.

Метод исследования, основанный на статистических испытаниях, получил название метода статистических испытаний или метода Монте-Карло.

Для реализации этого метода необходимо генерировать равномерно распределенные случайные числа.

На основе генерирования равномерно распределенных случайных чисел может решаться целый ряд задач.

Эти задачи разделяются на два класса:

• детерминированные;

• статистические задачи.

Метод решения этих задач единый, универсальный, называемый методом статистических испытаний, методом статистического моделирования, методом Монте-Карло.

Примерами решения детерминированных задач являются:

• вычисление числа ;

• вычисление сложных интегралов, которые не могут быть определены аналитическим путём.

П

R

N_к

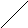
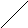
римеры представлены на рис.10.41.

N_кв

S_kв

S_ф

а) б)

Рис.10.41.Примеры вычисления числа(а) и площади сложной фигуры (б)

Задачи решаются следующим образом.

Проводятся эксперименты по попаданию точек на указанные фигуры

Если вероятность попадания точки в элементарный квадратик одинакова, то количество точек пропорционально площади.

При вычислении числа имеем состояние

,

где S_к– площадь четверти круга;

S_кв– площадь квадрата со стороной равнойR;

N_к– количество точек, попавших в четверть круга;

N_кв– количество точек, попавших в квадрат.

Поскольку

,

то

то

или .

При вычислении интеграла, как площади сплошной фигуры S_фимеем

.

Площадь квадрата S_кв известна. Определив количество точек, попавших на фигуруN_ф, и количество точек, попавших в квадратN_к, можно вычислить площадь фигурыS_ф

.

Метод Монте-Карло может применятся для решения задач оптимизации. В этом случае метод носит название метода случайного поиска.

Примерами использования метода Монте-Карло для решения статистических задач является статистическое моделирование, т. е. моделирование систем, на которые действуют входные статистические сигналы (например, входной поток заявок СМО) и характеристики состояния которых изменяются случайным образом. К числу таких систем относятся СМО.

При статистическом моделировании равномерно распределенные случайные числа могут подвергаться статистическим и динамическим преобразованиям.

К числу первых относится преобразование по методу обратных функций. Результатом этого преобразования является получение случайной величины, распределенной по определенному закону. Схема подобного преобразования с использованием обратной функции F^-1показана на рис.10.42.

Рис. 10.42.Схема преобразования с использованием обратной функции

Изменяя функцию распределения F, получаем случайные величины с различными законами распределения. Процесс получения обратных функцийF^-1представлен ниже.

Динамическое преобразование используется для получения случайных процессов с определенными характеристиками.

Схема преобразований имеет вид, показанный на рис.10.43.

Рис.10.43.Схема преобразования случайного процесса с использованием формирующего фильтра

В качестве формирующего фильтра, в частности, может быть использовано апериодическое звено с различными постоянными времени.