6. Разработка программы, реализующей алгоритм модели на компьютере.

7. Решение задач аналитическим или численным методом.

8. Анализ результата.

9. Принятие решения на основе результатов исследования.

10. Построение объекта и его апробация.

11. Корректировка модели.

12. Исследование на скорректированной модели.

13. Повторная корректировка объекта.

Рассмотрим указанные этапы моделирования на простейшем примере выбора характеристик системы наполнения инвестициями финансового фонда. Руководитель фонда приглашает для решения проблемы консультанта – аналитика. Консультант предлагает ему решить проблему путем математического моделирования, и получает согласие руководителя фонда.

Этап 1. Постановка задачи.Руководитель фонда дает характеристику той финансовой системы, которую ему необходимо создать, и формулирует основной вопрос, на который должно ответить математическое моделирование: ''Какова должна быть первоначальная плотность потока инвестиций, чтобы фонд заполнялся меньше, чем за два месяца?''

Этап 2. Построение информационной модели. Исходная финансовая система представляет собой систему управления поступлением инвестиций в фонд.

Предположим, что система функционирует как замкнутая система управления, в которой величина средств, поступающих в единицу времени, уменьшается по мере уменьшения рассогласования между требуемой и реальной величиной фонда. Тогда структура информационной модели имеет вид, представленный на рис. 2.3.

Информационная модель состоит из трех блоков:

ОУ – объект управления;

УС – управляющая система;

ОС – система обратной связи.

В числе переменных, связывающих блоки и характеризующих их входы и выходы:

x – входное задающее воздействие;

y – выходная величина;

e – рассогласование между входной и выходной величиной;

u – управляющее воздействие.

В экономических системах:

x – план;

y – реализация плана, его выполнение.

(-)

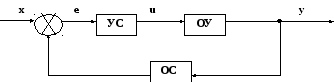
yос = y

Рис. 2.3.Структура информационной модели

Этап 3. Построение математической модели. Математическая модель управления наполнением резервуара будет определена, если записать алгебраические и дифференциальные уравнения каждого звена системы.

Пусть два звена, управляющая система и звено обратной связи, определены алгебраическими уравнениями.

1. Уравнение управляющей системы:

u = K ∙ e, (линейное звено с коэффициентом усиления K).

2. Уравнение обратной связи:

yос = 1 ∙ u, (линейное звено с единичным коэффициентом усиления).

3. Третье уравнение – уравнение суммирующего элемента.

y_oc = 1 ∙ y; e = x - yос. Т.к. y_ос = y, то можно записать, что

e = x – y.

4. Четвертое уравнение – это уравнение объекта управления. Объект управления представляет собой интегрирующее звено. Интегрирующие звенья широко распространенны в реальности. Примеры операции интегрирования:

• путь – интеграл от скорости;

• работа – интеграл от мощности;

• показание счетчика – интеграл от количества потребленной электрической энергии, газа или воды, в единицу времени;

• величина фонда – интеграл от количества финансовых средств, поступающий в единицу времени.

Итак, четвертое уравнение

y = ∫ u(t) ∙ dt.

Уравнение 4 можно записать в дифференциальной форме y' = u.

Уравнениям 1-3 соответствует одно уравнение

u=K (x – y).

В результате имеем систему двух уравнений – дифференциального и алгебраического:

у' = u;

u = K ∙ (x – y)

Исключая переменную u, приходим к одному уравнению

у' + K ∙ у = K ∙ x

Полученное уравнение и есть математическая модель процесса управления величиной фонда.

Данное уравнение может быть решено аналитически, т.е. получена формульная зависимость для у(t). Если уравнение модели не может быть решено аналитически, то решение может быть получено численными методами на компьютере. Изменяя величину К, можно на компьютере исследовать влияние этой величины на характер процессов в системе.

Если ввести обозначение T=, то имеем, чтоK=. Величина Т называется постоянной времени. Дифференциальному уравнению у' +∙ у =∙x соответствует структурная схема, представленная на рис. 2.4.

(-)

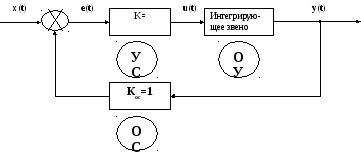
yoc(t)

Рис. 2.4.Структурная схема математической модели

Этап 4. Математический анализ уравнения модели. Полученное математическое уравнение

y' + ()y = ∙x

представляет собой линейное, неоднородное дифференциальное уравнение первого порядка с постоянным коэффициентами. Неоднородное, т.е. с правой частью, которая характеризует входное воздействие.

Однородное уравнение имеет вид:

у' + ∙y = 0.

Оно характеризует при заданном начальном уровне процесс уменьшения величины фонда.

Если уравнение имеет, например, вид:

у' + ∙ у² = x,

то это нелинейное уравнение. Уравнение модели является линейным.

Вывод:линейное дифференциальное уравнение математической модели может быть решено аналитически.

Этап 5. Получение исходной информации. Решение задачи будем рассматривать при следующей исходной информации:

1. Процесс увеличения величины фонда рассматривается при х=1.

2. Процесс уменьшения величины фонда исследуется при уо=1; х=0.

3. Согласно имеющейся информации параметр Т=1/d, где d – первоначальная плотность потока инвестиций.

Этап 6. Разработка программы. Программу составлять не нужно, т. к. возможно аналитическое решение.

Этап 7. Решение задачи. Известно, что общее решение неоднородного дифференциального уравнения есть сумма общего решения однородного дифференциального уравнения и частного решения неоднородного уравнения.

Находим общее решение однородного дифференциального уравнения.

у' + ∙ у = 0

Решение уравнения ищется в виде: у = e^αt .

Тогда у' = α ∙ e^αt . Подставляя у и у' в уравнение получаем:

α ∙ e^αt + () ∙e^αt = 0; или е^αt (α +) = 0.

Поскольку e^αt ≠ 0, то имеем:

α += 0 иα = –.

В результате получаем общее решение однородного уравнения в виде:

Y = С ∙ е^-t/Т, (2.1)

где С = соnst.

При единичном начальном условии имеем уравнение:

Y = е^-t/Т, (2.2)

Ищем частное решение неоднородного уравнения. Пусть начальные условия нулевые, т.е. у(о) = 0. Входное воздействие х = 1. Частное решение неоднородного уравнения, соответствующее условию у' = 0, есть у = х. Следовательно, у = 1 есть частное решение неоднородного уравнения.

Общее решение неоднородного уравнения имеет вид:

у = 1 + С ∙ е^-t/Т (2.3)

Константа С определяется из условия, что в момент t = 0 имеем у(о) = 0. После подстановки в уравнение величин t = 0 и y = 0 получаем:

у = С ∙ е⁰ + 1 = 0.

Т.к. у(0) = 0, то С ∙ 1 + 1 = 0. Следовательно, С = – 1.

В результате решение неоднородного уравнения при единичном входном воздействии записывается в виде:

у = 1 – е^-t/Т (2.4)

Этап 8. Анализ результата. Решение для однородного уравнения в виде (2.2) демонстрирует процесс уменьшения фонда. Уравнение (2.4) определяет процесс увеличения величины фонда. Соответствующий уравнению (2.4) процесс увеличения фонда имеет вид, показанный на рис. 2.5.

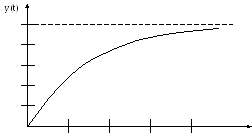
1

Т = 0,5

0,5 1 1,5 2 t

Рис. 2.5. Процесс увеличения финансового фонда по апериодическому закону

Переходный процесс в данной системе заканчивается за время, равное примерно трём постоянным времени системы. Если Т = 1мес., то процесс длится порядка 3 месяца. Через 3 месяца величина у(t) будет отличаться от требуемого значения у = 1 не более чем на 5%.

Согласно предъявленным требованиям процесс заполнения фонда должен быть не более 2-х месяцев. Известно, что постоянная времени Т = 1/d, гдеd– первоначальная плотность потока инвестиций. Приd= 1, имеем время заполнения Т = 3 мес., еслиd= 2, то Т = 1,5 мес.

При наличии двух вариантов плотности потока (d = 2иd =1 ) предъявленному требованию, состоящему в том, что время процесса составляет меньше двух месяцев, удовлетворяет плотность потокаd = 2.

Этап 9. Принятие решения. Для простых систем по результатам моделирования принимается решение о реализации объекта.

Для сложных систем, например при создании летательных аппаратов, первоначально по результатам проектирования принимается решение о строительстве образца объекта.

Этап 10. Построение объекта и его апробация. В ходе испытаний объекта проверяется соответствие реальных характеристик предъявленным требованиям.

Этап 11. Корректировка модели. Если реальные характеристики не удовлетворяют требованиям, что повторяется весь указанный цикл.

Таким образом, для сложных систем процесс моделирования является итеративным.