3.5.2. Статистические методы регулирования технологических процессов

Эти методы используются только в процессах управления качеством. Необходимость в регулировании технологических процессов возникает вследствие износа инструментов, оснастки, оборудования, самоотвинчивания гаек под воздействием вибрации, старения элементов конструкции оборудования, а также вследствие других физических явлений.

Статистические методы регулирования технологических процессов основаны на контроле мгновенных выборок, каждая из которых представляет собой совокупность значений параметров или качественных признаков небольшого числа (обычно, не более десяти) единиц продукции, отбираемых подряд сразу после определенной технологической операции. Контроль выборок осуществляется через установленные интервалы времени, обычно периодически. По результатам контроля принимаются решения о смене инструмента или оснастки, подналадке оборудования, вызове ремонтной бригады. Технологический процесс при этом чаще всего подлежит остановке. Грамотное применение статистических методов регулирования позволяет вовремя принимать решения, снизить ошибки первого и второго рода при принятии решений.

Основным инструментом статистических методов регулирования являются так называемые контрольные карты. Каждая из них соответствует одной или двум конкретным статистикам, выбираемым за показатель качества процесса в фиксированный момент времени. Контрольные карты делятся на две группы: карты по качественному признаку и карты по количественному признаку. Среди карт по качественному признаку выделяют карты групп качества, остальные – это карты по альтернативному признаку: q-карты (уровня дефектности), nq-карты (числа дефектных единиц продукции), c-карты (числа дефектов), u-карты (числа дефектов на единицу продукции).

Карты по количественному признаку тоже делятся на две группы: ординарные и комбинированные. Существует 4 типа ординарных карт: карты средних арифметических значений, индивидуальных значений, медиан, балловых оценок. Комбинированных карт также 4 типа: средних арифметических значений и средних квадратичных отклонений, средних арифметических значений и размахов, медиан и размахов, медиан и индивидуальных значений. Комбинированные карты – это, по сути, пары карт, за исключением карты медиан и индивидуальных значений.

Каждая контрольная карта предназначена для отражения изменения во времени (от выборки к выборке) значений той или иной статистики. На карту нанесены одна или две (верхняя и нижняя) границы регулирования. При выходе значения статистики за границу регулирования принимают решение о применении того или иного способа регулирования технологического процесса. Некоторые карты имеют дополнительно предупреждающие границы. Если точка вышла за эти границы, но не вышла за границы регулирования, то технологический процесс продолжается, но за ним устанавливается пристальное наблюдение.

На рис. 7 приведена заполненная контрольная карта средних арифметических значений без предупреждающих границ. На этом рисунке применены следующие обозначения: T_в, T_н – верхняя и нижняя границы поля допуска параметра х, Р_в, Р_н – верхняя и нижняя границы регулирования для среднего арифметического а – средняя линия. После получения последней точки принимается решение о регулировании технологического процесса.

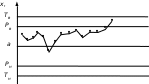
Рис. 7. Заполненная карта средних арифметических значений

Перед внедрением статистических методов регулирования возникает необходимость в определении планов контроля (объема выборок, границ регулирования, периодичности контроля или межконтрольных временных интервалов) с целью установления их в технологической документации. Существует множество различных методов определения планов контроля, вплоть до методов, позволяющих определять экономически оптимальные планы контроля. Однако в большинстве случаев применяют эмпирические и полуэмпирические методы.

На полуэмпирических методах определения планов контроля основаны стандартизованные на международном уровне контрольные карты Шухарта [46]. Строго говоря, этот метод следовало бы назвать «методом Шухарта по расчёту границ регулирования», так как сами карты – стандартные. Здесь предполагается объем выборки n задавать из эмпирических (на основе опыта) соображений. Границы же регулирования требуется вычислять на основе метода проверки статистических гипотез, предполагающего считать техпроцесс налаженным лишь в случае, когда значение некоторой вероятностной характеристики точно равно заданному значению.

В частности, для карты средних арифметических значений их предлагается вычислять по формулам: Р_в = a + z_ / Р_н = a – – z_ / где объем выборки обычно 3  n  7,  – среднее квадратичное отклонение мгновенного нормального распределения (считается величиной постоянной), z_ – квантиль стандартного нормального распределения, соответствующий малой вероятности  того, что среднее арифметическое в мгновенной выборке, взятой из генеральной совокупности, имеющей математическое ожидание a, окажется за пределами границ регулирования. Величина z_ является корнем уравнения: = 1 –  (при z_ = 3  = 0,0027; при  = 0,01 z_ = 2,576).

Величина , являющаяся условной вероятностью ошибочного решения, называется вероятностью ошибки первого рода, или риском излишней настройки. Иначе говоря,  – вероятность того, что будет принято решение о настройке процесса с мгновенным средним, равным середине поля допуска.

Заметим, что при увеличении объема выборки коридор между границами регулирования сужается, хотя такое увеличение, приводящее к росту информации, казалось бы, должно расширять этот коридор. Такая нелогичность связана с неявным предположением, что налаженным считается только такой техпроцесс, когда математическое ожидание мгновенного распределения равно а.

Для определения границ регулирования в карте средних арифметических значений применяются и такие формулы: Р_в =T_в – A; Р_н = T_р + A, где А – коэффициент, зависящий от объема выборки и риска . Однако в их основе лежит все то же предположение.

В этом – основной недостаток метода расчета границ регулирования, применяемого в контрольных картах Шухарта. В действительности всегда существует некоторый интервал значений некоторой вероятностной характеристики, при которых процесс считается налаженным. Поэтому более предпочтителен другой метод, также основанный на теории проверки статистических гипотез. Он аналогичен методу определения плана статистического приемочного контроля (см. п. 2.4.3).

В частности, для карты средних арифметических значений задается интервал [a_н;a_в] (он чаще всего симметричный относительно а), риск излишней настройки , а также риск незамеченной разладки  и величины a_н; a_в, такие, что a_н  a_н, a_в  a_в. При этом наряду с границами регулирования определяется и объем выборки. Уравнения для определения верхней границы регулирования и объема выборки имеют вид: Р_в = a_в + z_ / Р_в = a_в – z_ /

Аналогично можно записать уравнения для определения нижней границы регулирования и объема выборки. При симметричном расположении величин a_н,a_в, а также a_н;a_в относительно а границы регулирования также будут симметричны относительно а.