2.3.3. Расчетно-экспериментальные методы оценивания параметров

В случаях, когда экспериментальные методы оценивания очень неточны (мал объем выборки, мало время испытаний и пр.), но имеются результаты расчетов или имеется определенный опыт эксплуатации или испытаний аналогичных изделий, или выявлены причины, породившие низкое качество продукции, и найдены способы их устранения, специалисты могут использовать эту априорную (дополнительную) информацию для уточнения результатов оценивания, полученных экспериментальным путем. Иначе говоря, определяют так называемую объединенную (точечную или интервальную) оценку группового параметра h, под которым понимается параметр или числовая характеристика (обычно – математическое ожидание или вероятность) известной функции распределения F(x) некоторой случайной величины Х (например, предела прочности, наработки до отказа, бинарной случайной величины, принимающей значения 0 или 1, в зависимости от того, произошел отказ за время испытаний или нет), определенной на некоторой совокупности единиц продукции . Имеется два подхода к такому объединению.

Первый подход основан на приведении (с помощью экспертной корректировки) точечных оценок, полученных на основе расчетов и эксплуатации или испытаний (измерений) аналогичных изделий, и их дисперсий к генеральной совокупности . С помощью такой корректировки все точечные оценки стремятся сделать несмещенными оценками h₁,h₂, h_m параметра h. Каждая из оценок рассматривается как полученная на основе выборки, извлеченной из одной и той же генеральной совокупности . Пусть – скорректированные дисперсии (или оценки дисперсий) точечных оценок параметра. Объединенная точечная оценка параметра и ее дисперсия имеют вид (в классе линейных оценок) [33]:

где

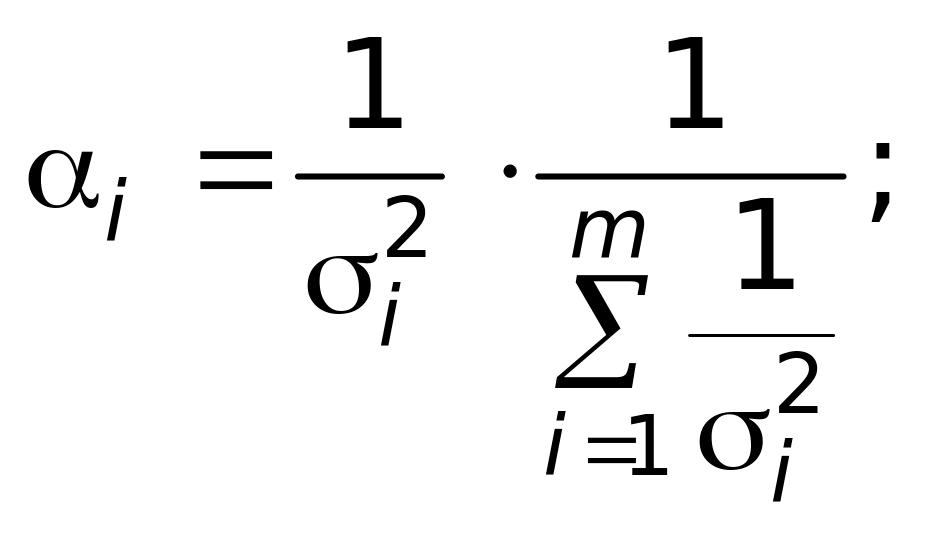
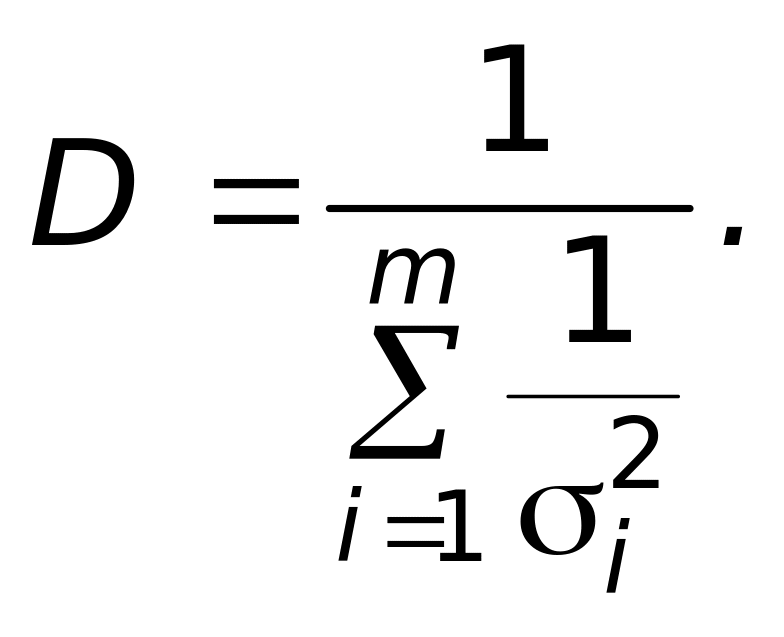
Зная дисперсию (или ее оценку) объединенной точечной оценки, можно найти и интервальную оценку параметра для конкретного распределения F(x).

Второй подход (байесовский метод) основан на предположении, что априорную информацию можно использовать для определения априорной плотности вероятности w(h). При этом h рассматривается как случайная величина (Н) на совокупности совокупностей ₁, ₂, ... _ (например, гипотетической совокупности партий продукции, каждая из которых может быть произведена при использовании несколько иных конструкторских или технологических решений), в каждой из которых вид распределения случайной величины Х – один и тот же. Точечную оценку, полученную экспериментальным путем, обозначают обычно или (как случайную величину) Ее можно рассматривать как несмещенную оценку параметра h одной из совокупностей _i. Тогда, как правило, не составляет труда получить выражение для условной плотности вероятности f( /h) (если случайная величина является непрерывной) либо условной вероятности Р( /h) (если случайная величина является дискретной). Идея байесовского метода оценивания состоит в использовании формулы Байеса, связывающей априорное и апостериорное (т.е. после получения экспериментальной информации) распределения:

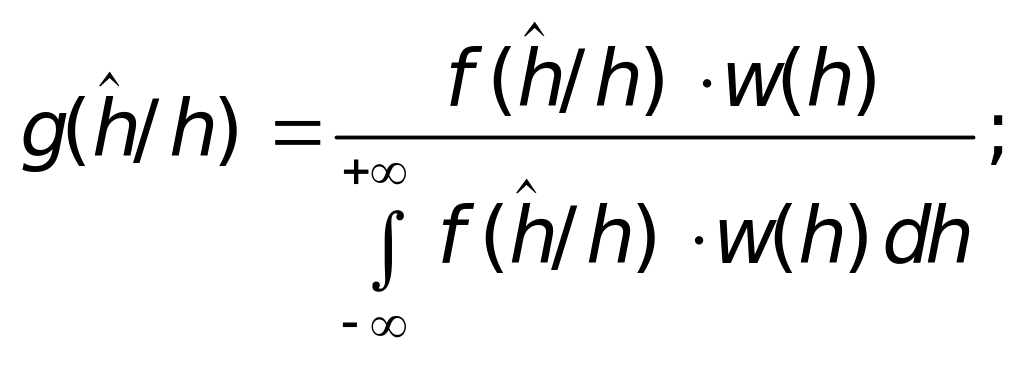или

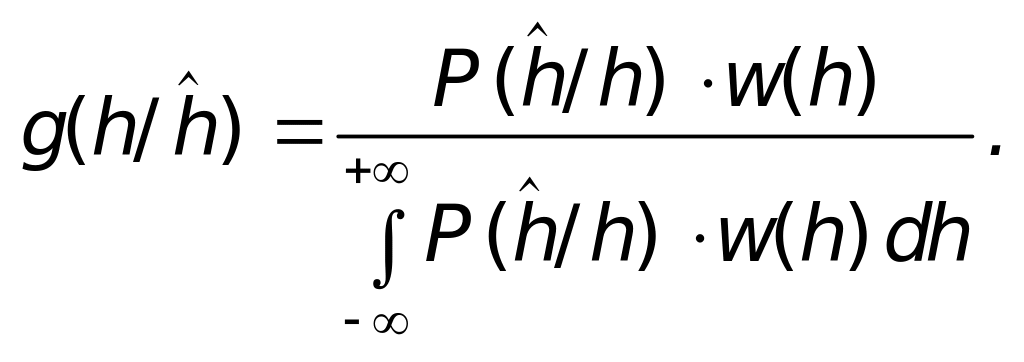
Эти формулы записаны в предположении, что если функция распределения F(x) имеет больше одного параметра, то остальные (кроме h) должны быть постоянными. Байесовские оценки в общем случае зависят от выбираемой функции потерь, обусловленных ошибочным оцениванием [34]. Обычно (при квадратичной функции потерь) в качестве объединенной точечной оценки берут условное (апостериорное) математическое ожидание случайной величины Н:

Объединенная интервальная оценка: где и – верхний и нижний квантили нормированного апостериорного распределения, соответствующие заданной вероятности р нахождения истинного значения параметра в указанном интервале, а _апс – условное среднее квадратичное отклонение случайной величины Н, определяемое как квадратный корень из дисперсии:

Основная проблема здесь – определение априорного распределения. Если априорная информация задана в виде точечных оценок представляющих разные совокупности _i, но имеющих одну и ту же дисперсию, то, строя гистограмму, можно оценить безусловную плотность вероятности Априорное распределение w(h) является решением интегрального уравнения:

Если h – математическое ожидание нормально распределенной случайной величины Х в совокупностях _i, дисперсия случайной величины Х одна и та же и равна ², – среднее арифметическое, определяемое по выборке объема n, – нормальное распределение, то и w(h) – тоже нормальные распределения, математическое ожидание априорного распределения равно математическому ожиданию безусловного распределения, а между дисперсиями существует следующая связь: