Решение Вариант 1

Вращающий момент на входном валу Т₁ = , где

угловая скорость вращения ω_э = = 314 рад/с.

Тогда Т₁ = = 9,55 Н·м.

Вращающий момент на выходном валу

Т₂ = Т₁ u η.

По рекомендациям КПД зубчатой передачи η = 0,98.

Тогда Т₂ = 9,55·5·0,98 = 46,8 Н·м.

Вариант 2

Вращающий момент на выходном валу Т₂ = Р_вых / ω_вых,

где мощность на выходе Р_вых = Р_эη = 3 · 0,98 = 2,94 кВт.

Угловая скорость вращения на входном валу

ω_э = ω_вх = = 314 рад/с.

Угловая скорость вращения на выходном валу

ω_вых = =62,8 рад/с.

Тогда Т₂ = = 46,8 Н·м.

Пример 3.3. (рис.3.21). Определить межосевое расстояние цилиндрической прямозубой передачи привода и силы в зацеплении, если число зубьев шестерни z₁ из условия неподрезания минимальное, окружной шаг р = 12,56 мм; передаточное число u = 5; вращающий момент на колесе Т₂ = 46,8 Н·м.

Решение

Межосевое расстояние а = .

Делительный диаметр колес d₁ = m z₁; d₂ = m z₂,

где z₁ = z_min = 17; z₂ = z₁· u = 17·5 = 85.

Модуль зацепления m = p/π = 12,56 /3,14 = 4 мм;

d₁ = 4·17 = 68 мм; d₂ = 4 · 85 = 340 мм.

а = = 204 мм.

Силы в зацеплении:

oкружная F_t = = 275 Н;

радиальная F_r = F_t tgα = 275·0,364 = 100 Н;

где α = 20⁰ – стандартный угол зацепления.

Пример 3.4. (рис.3.21).

Определить межосевое расстояние цилиндрической косозубой передачи привода и силы в зацеплении по данным примера 3.3., принимая число зубьев шестерни z₁ = 17, угол наклона зубьев β = 14⁰.

Решение

Межосевое расстояние а = .

Делительные диаметры колес:

d₁ = = 70 мм

d₂ = = 350 мм.

а = = 210 мм.

Силы в зацеплении:

oкружная F_t = = 266 Н.

радиальная F_r = = 99,8 Н;

осевая F_a = F_t tgβ = 266·0,249 = 66 Н.

Пример 3.5. (Рис. 3.22).

Рис. 3.22

Определить межосевое расстояние червячной передачи с однозаходным червяком, если передаточное число u = 30, шаг зацепления р=25,12 мм, коэффициент диаметра червяка q = 10. р=25,12 мм, коэффициент диаметра червяка q = 10.

Решение

Межосевое расстояние а = .

Модуль m = = 8 мм.

Делительный диаметр червяка d₁ = mq = 8·10 = 80 мм.

Делительный диаметр червячного колеса d₂ = mz₂,

где z₂ = z₁u = 1 · 30 = 30.

С учетом этого d₂ = 8 · 30 = 240 мм и а = =160 мм.

3.7. Понятие о винтовых, фрикционных, ременных и цепных передачах

3.7.1. Винтовые передачи

Винтовая передача или передача винт-гайка предназначена для преобразования вращательного движения поступательное.

Простейший механизм содержит два звена: винт – цилиндрический стержень с резьбой и гайка – обычно втулка с внутренней резьбой (рис.3.23).

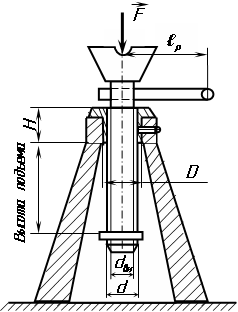
Рис.3.23

Оба звена составляют пару, в которой задается либо вращение гайки, приводящее к поступательному движению винта, либо вращение винта, приводящее к поступательному движению гайки. В зависимости от особенности конструкции обе возможности получили распространение.

Для винтовых механизмов используется прямоугольная симметричная и трапецеидальная несимметричная (упорная) резьбы. Резьба винтов и гаек передач может быть правой или левой, однозаходной и многозаходной. Для самотормозащих передач используют однозаходную резьбу.

В последнее время стали применять передачи винт-гайка, в которых трение скольжения заменено трением качения, шариковые винтовые пары. Такая передача состоит из винта, гайки и шариков, заполняющих пространство, образованное впадинами резьбы. Перемещение шариков происходит по замкнутому каналу, соединяющему первый и последний витки резьбы гайки.

Винты передачи без термообработки изготовляют из стали 45, 50, а с закалкой – из стали 65Г, 40Х, 40ХГ и др. с закалкой до твердости более 50 НРС. Для уменьшения трения и износа резьбы гайки передачи изготовляют из бронз Бр010Ф1, Бр06Ц603 (при высоких скоростях вращения υ₃ = 0,1-0,25 н/с) и антифрикционных чугунов АВ4-1, АВ4-2, АК4-1, С415 и др. при малых скоростях).

Достоинства: простота конструкции, плавность и точность хода, большая несущая способность, большое передаточное отношение, самоторможение.

Недостатки: сравнительно невысокий КПД.

Передачи винт-гайка применяют в самых различных конструкциях как, например, в подъемно-транспортных машинах (домкраты, опоры), в станках (механизм подачи рабочих инструментов), в измерительных приборах. В артиллерийской технике они используются в механизмах наведения и прицеливания.

В винтовых механизмах вращение винта или гайки осуществляют обычно с помощью маховика, шестерни и т.п. при этом передаточное отношение обычно можно выразить отношением окружного перемещения маховика S_М и перемещением гайки (винта) S_Г

ί = , (3.65)

где d_M – диаметр маховика (шестерни и т.п.);

р - шаг резьбы;

z – число заходов винта.

Зависимость между окружной силой F_t на маховичке и осевой силой F_a на гайке (винте) записывается в виде

F_t = F_a ί η, (3.66)

где η – КПД винтовой пары.

В свою очередь, коэффициент полезного действия (КПД) определяется соотношением

η = , (3.67)

где β = zρ/πd₂ – угол подъема резьбы;

ρ – угол трения.

Обычно η ≤ 0,7 и лишь для шариковых винтовых пар повышается до η = 0,9.

Основным критерием работоспособности передачи является износостойкость. Величиной, ее характеризующей, принимают напряжения смятия σ_СМ, которые должны удовлетворять условию прочности на смятие

σ_СМ = ≤ [σ_СМ], (3.68)

где d₂ – средний диаметр резьбы;

h – высота рабочего профиля резьбы;

z – число витков резьбы в гайке.

Для пар материалов винт-гайка сталь-броза [σ_СМ] = 10-13 МПа, сталь-чугун [σ_СМ] = 5-6 МПа.

Винт механизма находится в состоянии сложного сопротивления, так как он испытывает деформацию растяжения-сжатия и деформацию кручения. Условием прочности является

σ_экв ≤ [σ], (3.69)

где эквивалентные напряжения определяются по формулам сопротивления материалов. В случае, когда длина винта достаточно велика, и он находится в состоянии сжатия, его необходимо рассчитывать на устойчивость.