Решение систем линейных уравнений с – неизвестными

Система – линейных уравнений с – неизвестными , , … может быть записана в общем виде так: (1)

Где – коэффициенты, – свободные члены ( – номер строки, – номер столбца). Соответствующий определитель запишем так:

Определение:  Минором любого элемента этого определителя называется определитель -го порядка, соответствующий матрице, полученной из данной вычеркиванием строки и столбца, в которых лежит указанный элемент. Минор элемента будем обозначать .

Определение:  Алгебраическим дополнением любого элемента определителя называется его минор , взятый со знаком числа .

Алгебраическое дополнение элемента будем обозначать . Таким образом,

Можно доказать теорему:  Если определитель системы (1) отличен от нуля, то эта система совместна и определена, причём её единственное решение может быть найдено по формулам Крамера: ; ; …, .

Если же , то система либо не совместна, либо имеет бесчисленное множество решений.

Пример 8.  Решить систему уравнений:

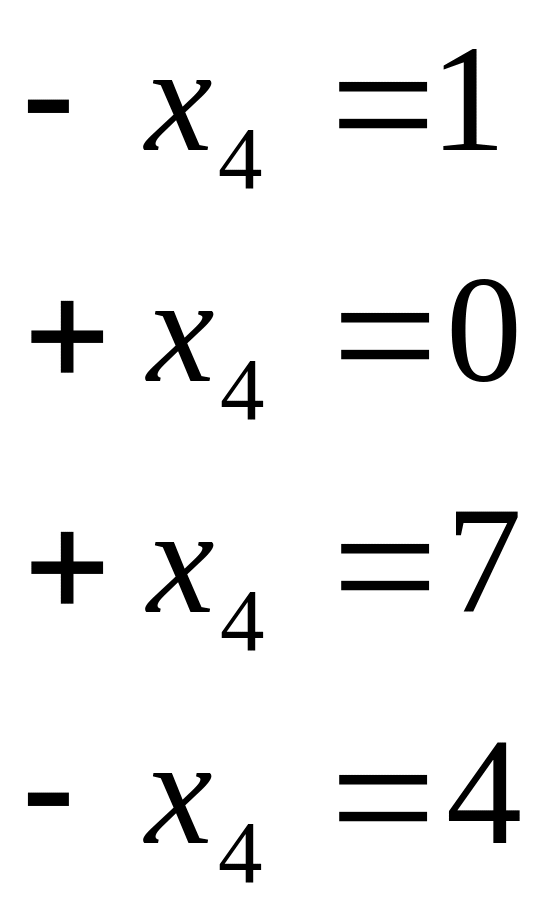
Система совместна, т.к.

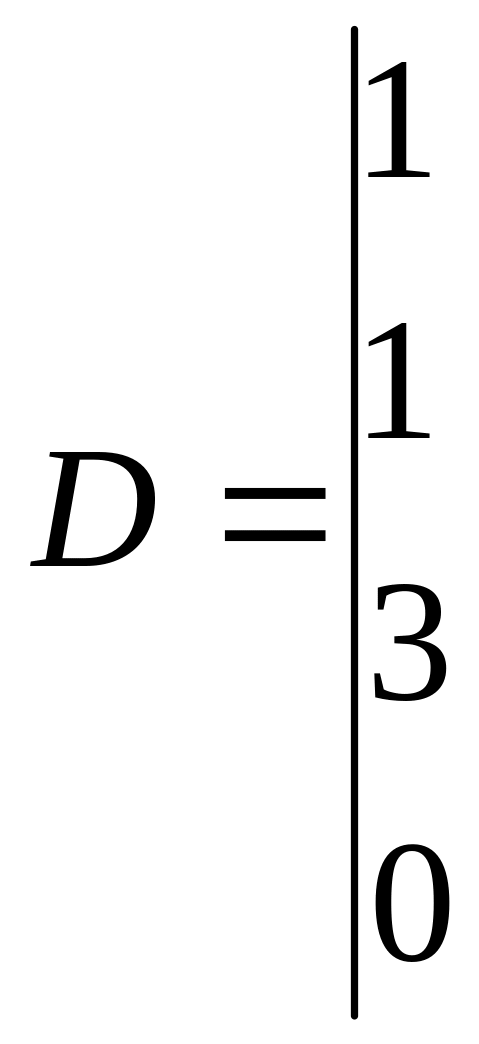
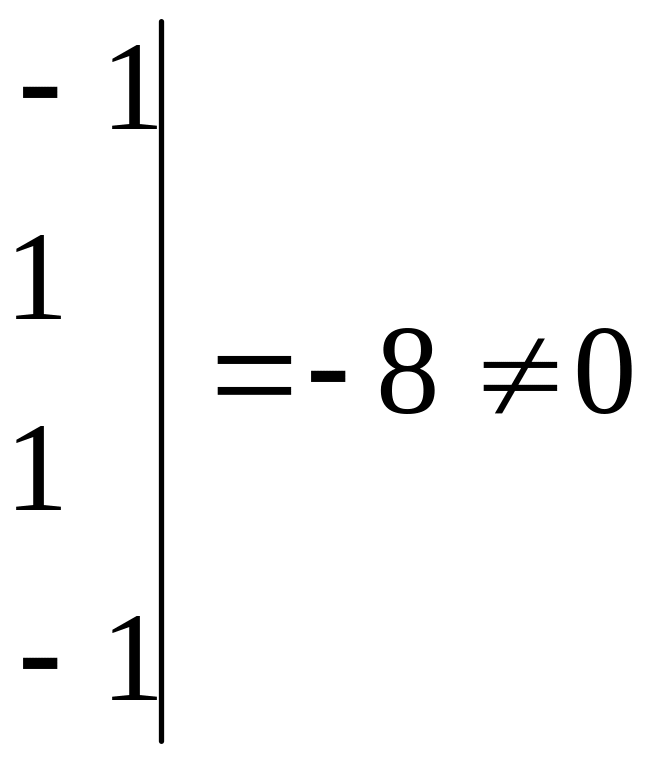
Вычисляя , , , , получаем:

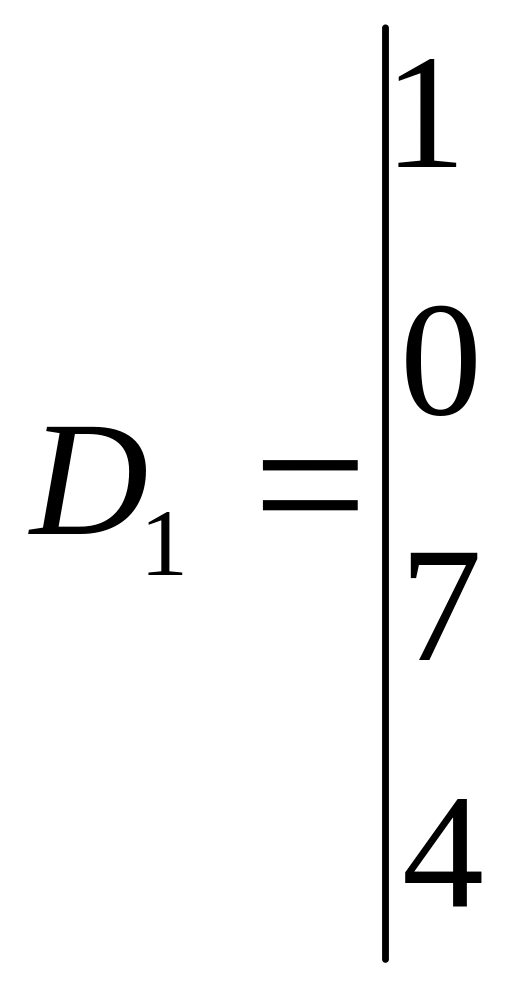
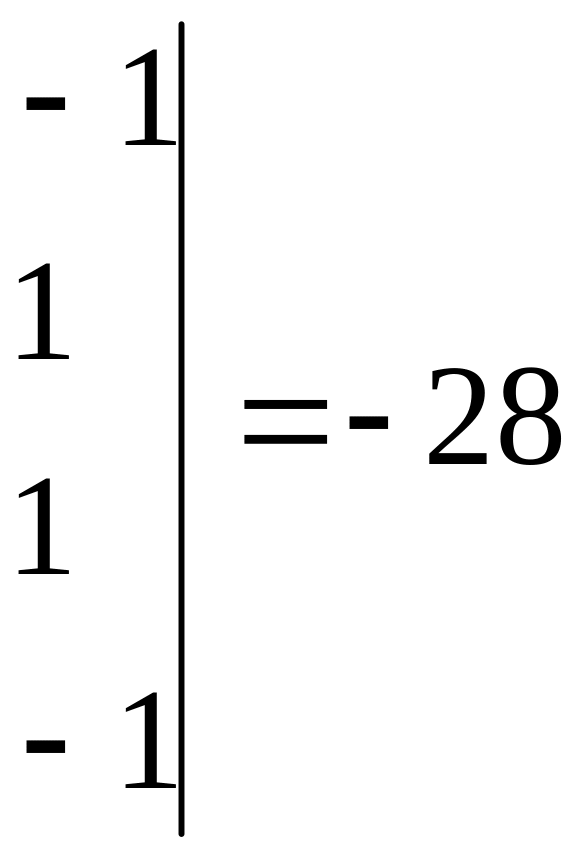
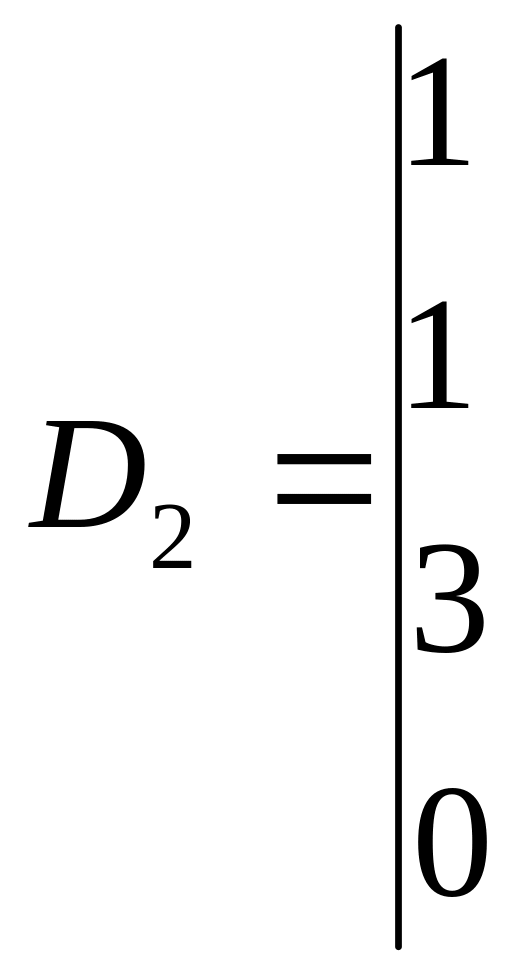
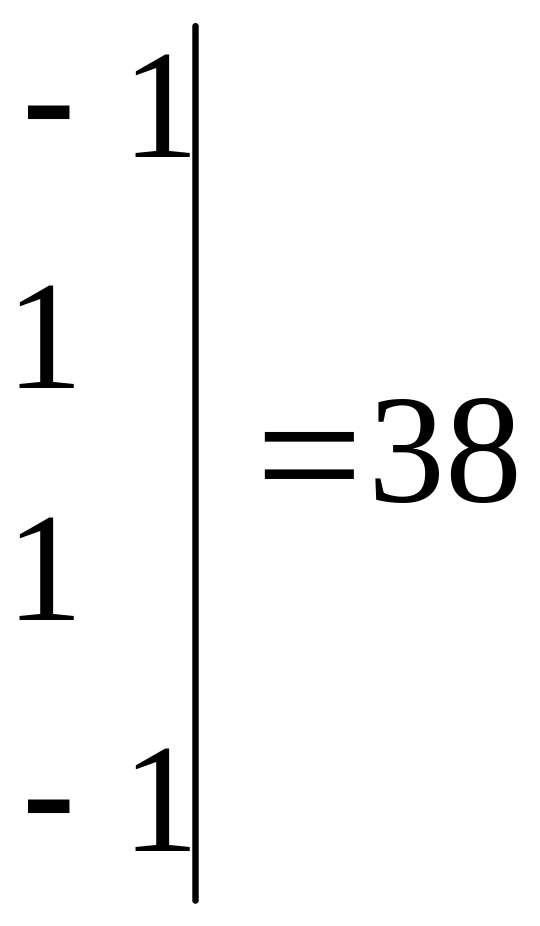
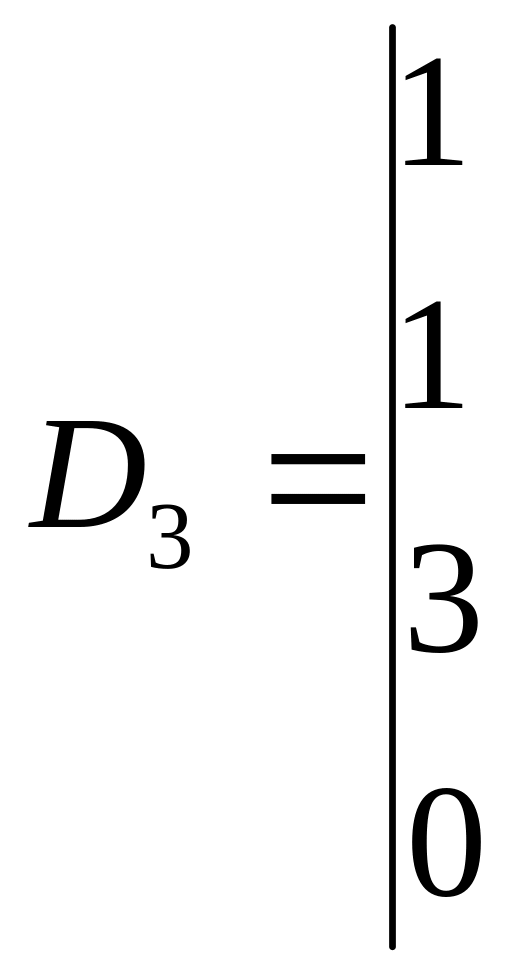
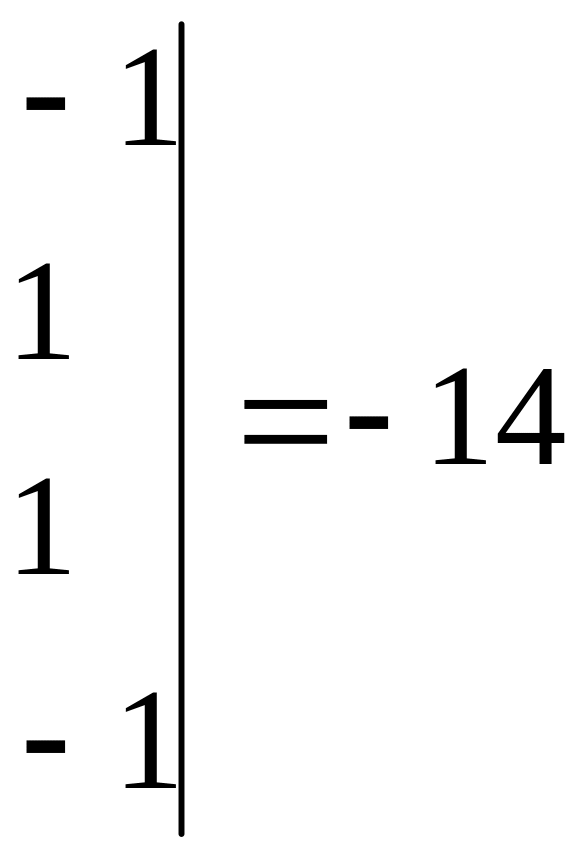
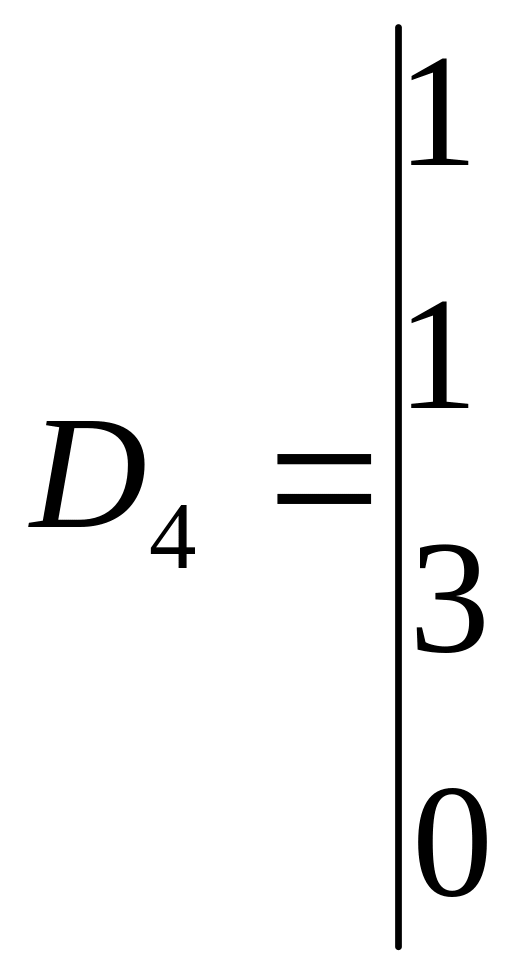
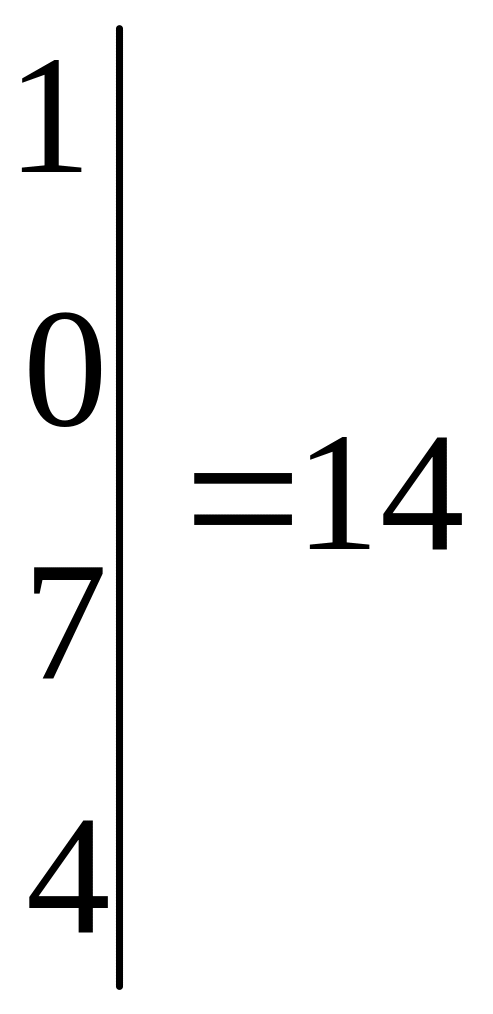
Следовательно, , , , – решение системы.

Другим эффективным методом решения систем линейных уравнений является метод исключения неизвестных, называемый также методом Гаусса. Он состоит в том, что данная система линейных уравнений преобразуется в равносильную ей систему специального вида, которая легко исследуется и решается.

С помощью элементарных преобразований любую систему линейных уравнений можно преобразовать так, чтобы некоторое фиксированное неизвестное , сохранившись в одном уравнении системы, исключалось из любого другого. Для этого достаточно подобрать соответствующее значение множителя для каждого уравнения, из которого выбранное неизвестное исключается. Такое преобразование системы линейных уравнений называется исключением неизвестного .

Пример 9.  Решить систему линейных уравнений:

Примем за первое ведущее уравнение первое уравнение системы, за первое ведущее неизвестное – ; первым ведущим элементом будет . Исключим из 2-го и 3-го уравнений, прибавив к ним ведущее уравнение, умноженное соответственно на и . Получим:

За второе ведущее уравнение примем второе уравнение системы, а  за второе ведущее неизвестное – , вторым ведущим элементом будет . Исключим из третьего уравнения, получим:

обратным ходом получаем

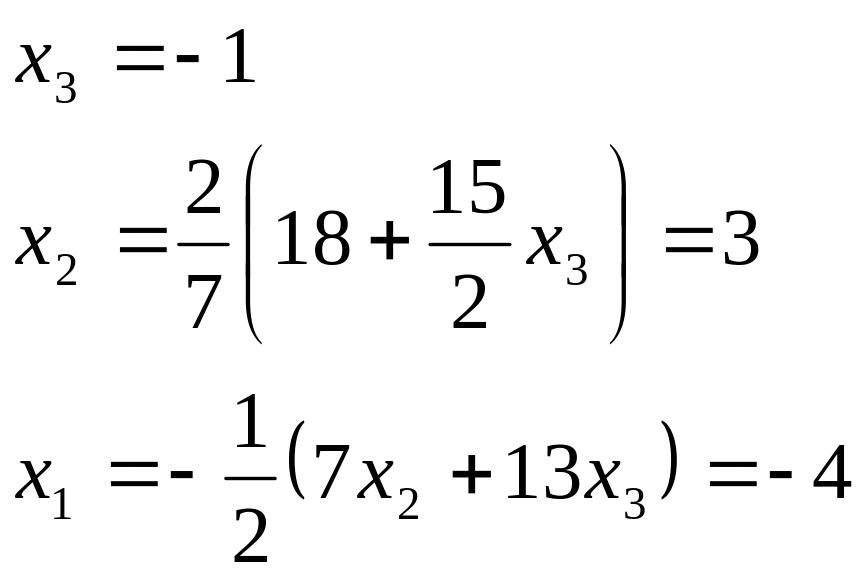
Решением данной системы будет: , , . В данном случае , решение единственное.

Если же ранг системы меньше числа неизвестных ( ), то система имеет много решений.

Рассмотрим решения типовых заданий по теме «Линейная алгебра»

Задание 1.

Даны две матрицы и . Найти: а)   ; б)   ; в)   ; г)   .

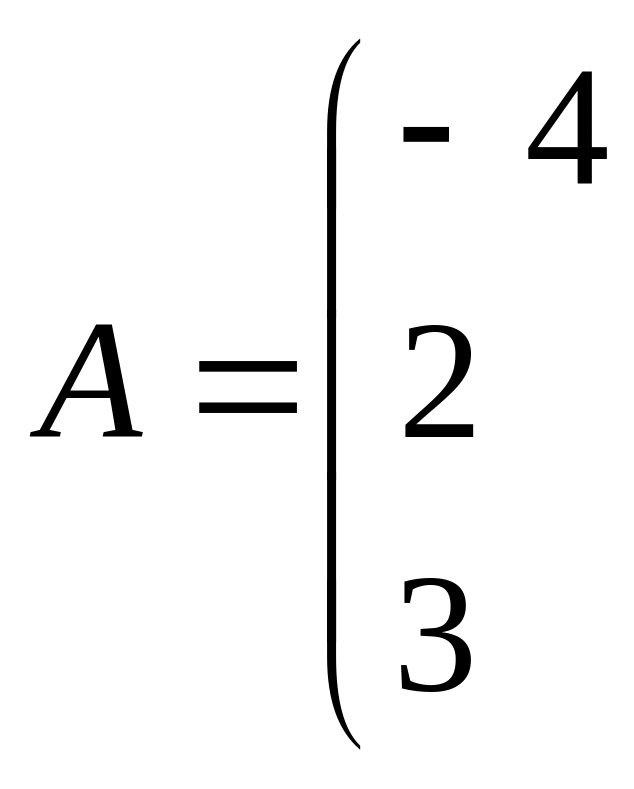
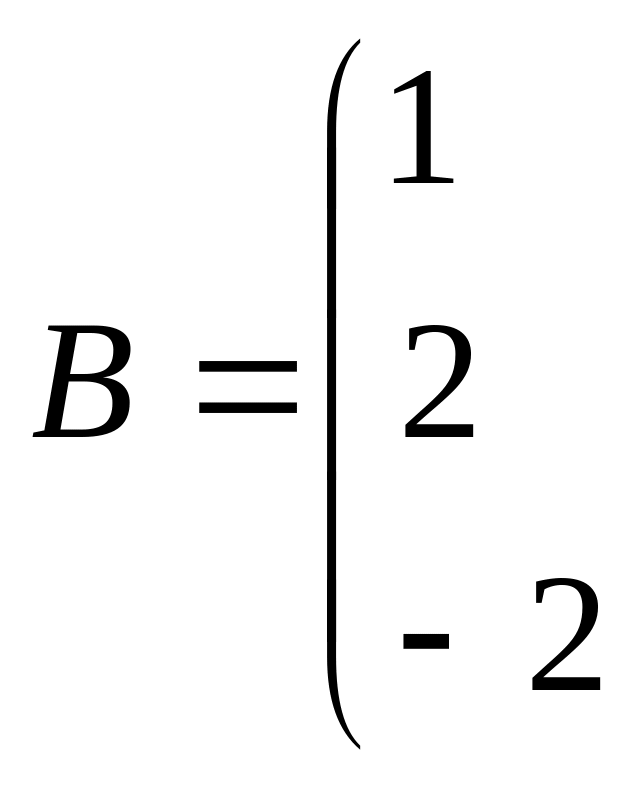
Решение:

а)  Произведение имеет смысл, так как число столбцов матрицы равно числу строк матрицы . Находим матрицу ,  элементы которой определяются по формуле

Имеем

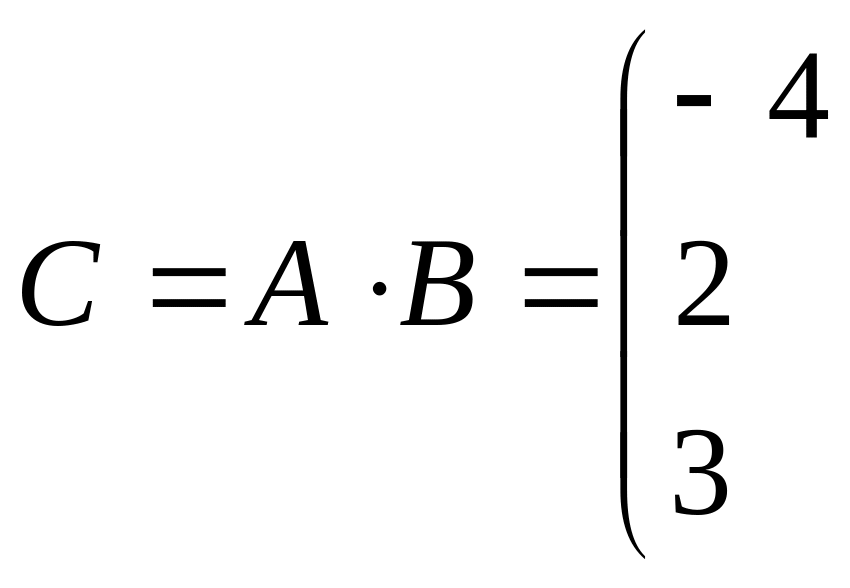
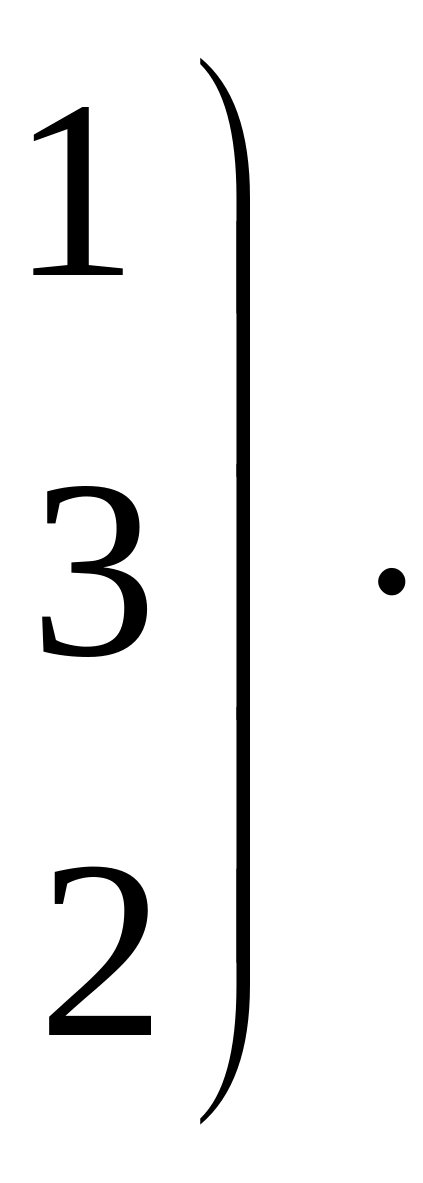
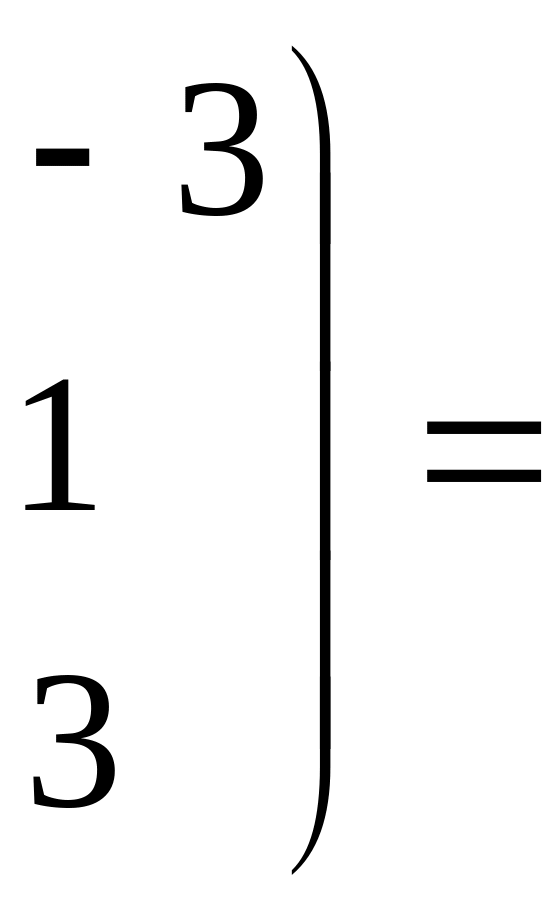
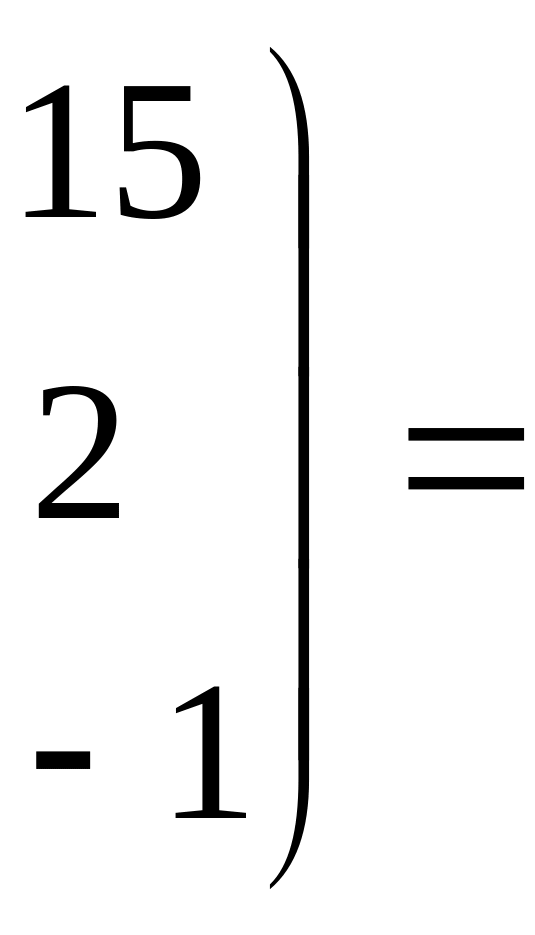
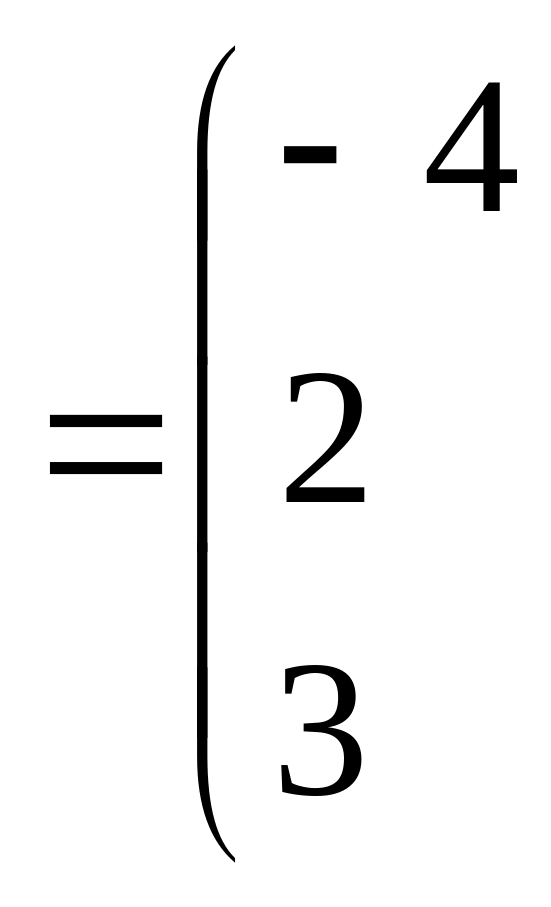
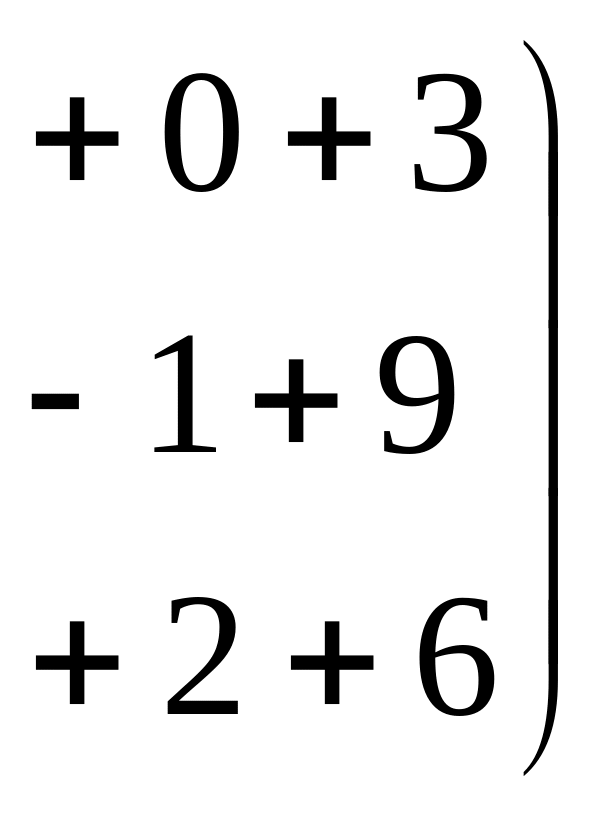
б)  Вычислим

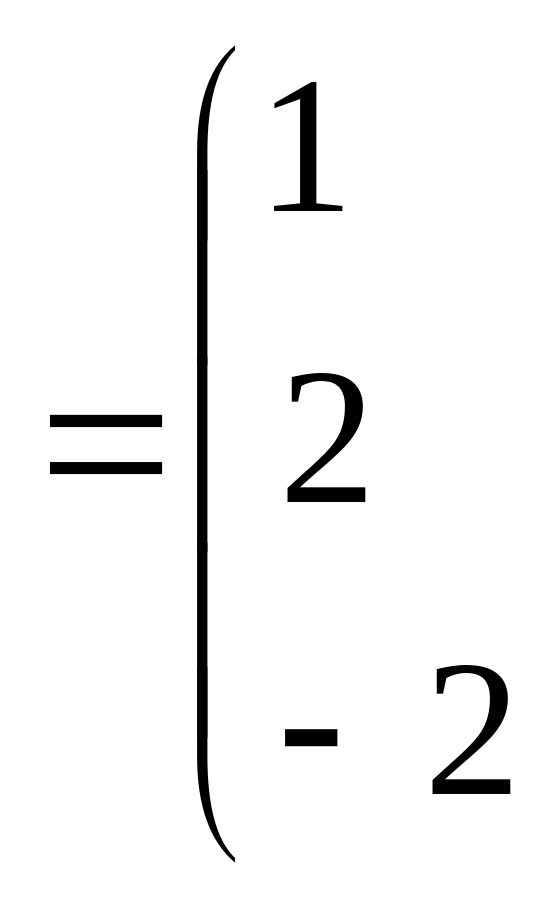
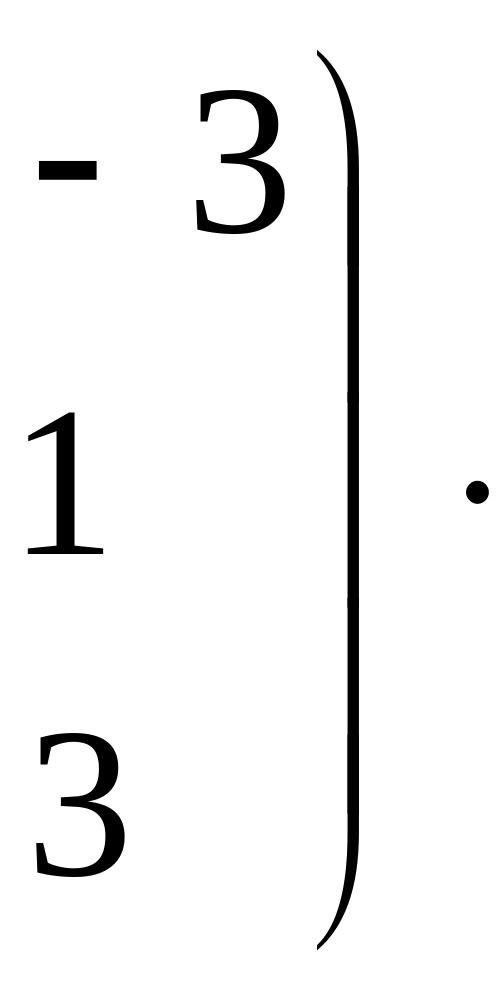
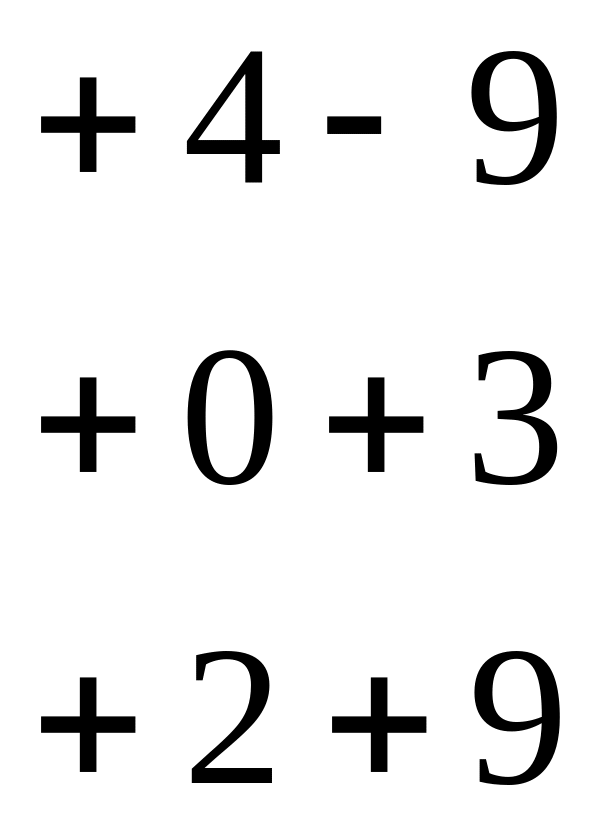
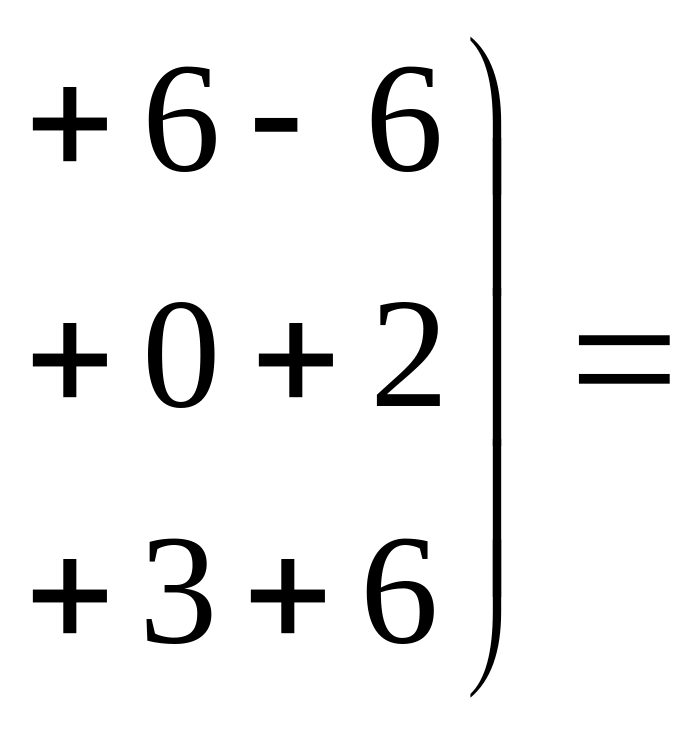
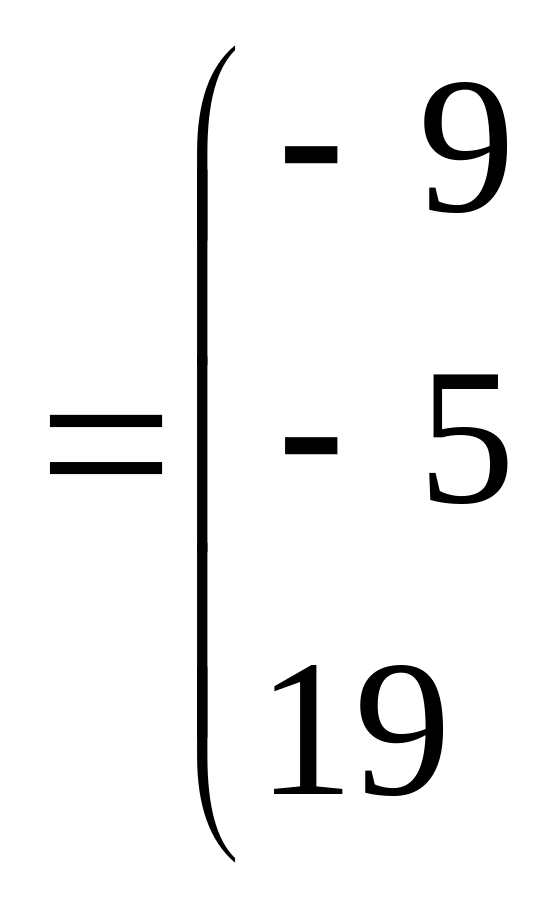
Очевидно, что ;

в)  Матрица называется обратной по отношению к матрице , если , где – единичная матрица

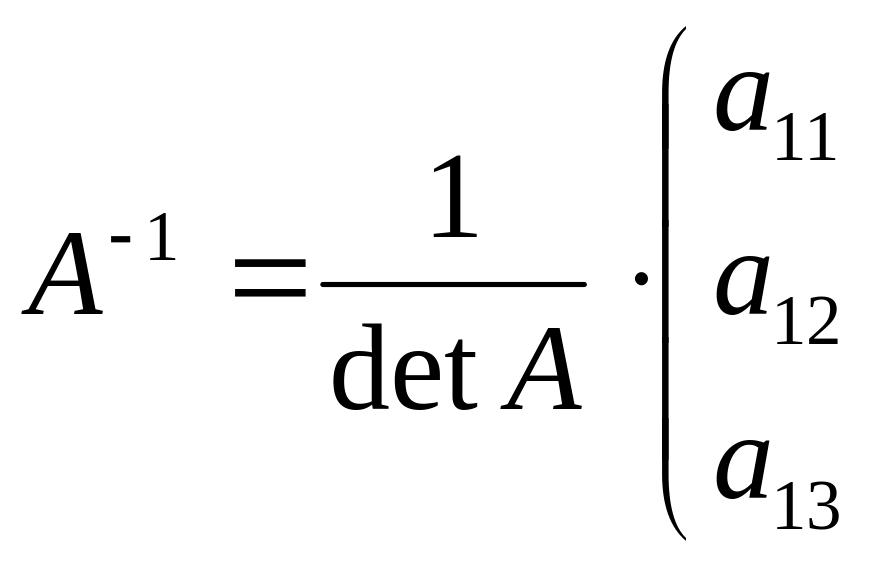
Обратная матрица матрицы имеет вид , где

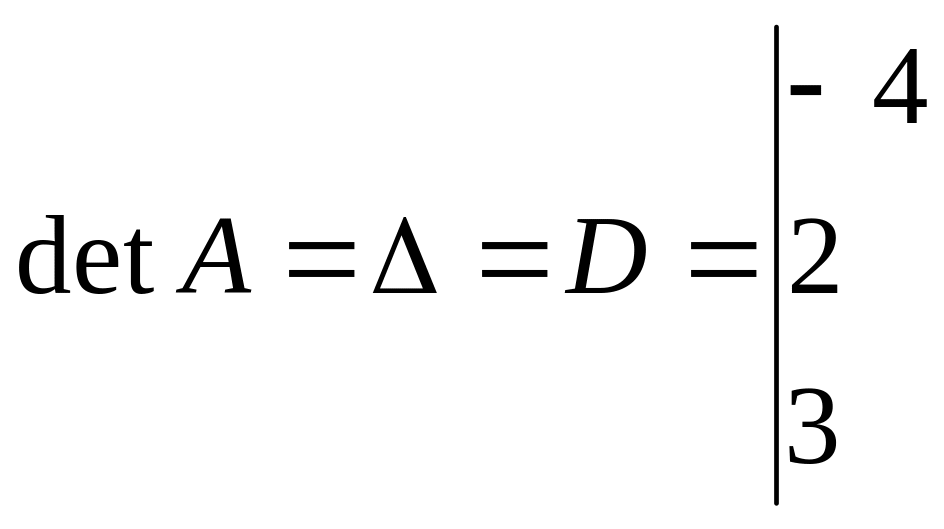
, т.е. матрица невырожденная, и, значит, существует матрица . Находим: , ,

, , , ,

, , .

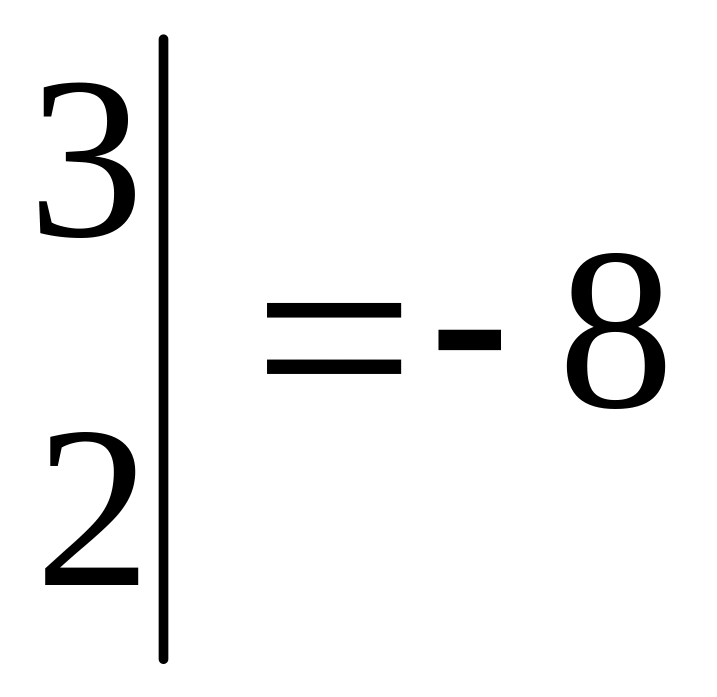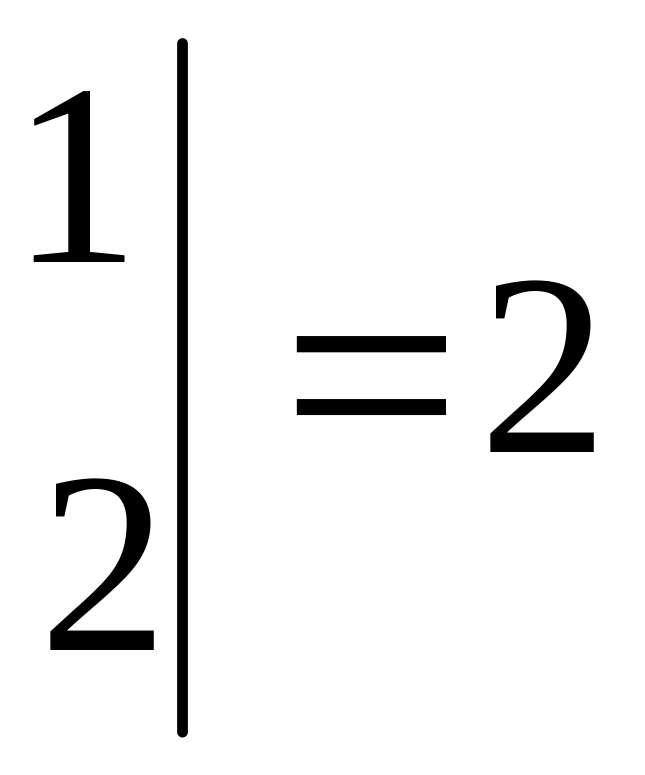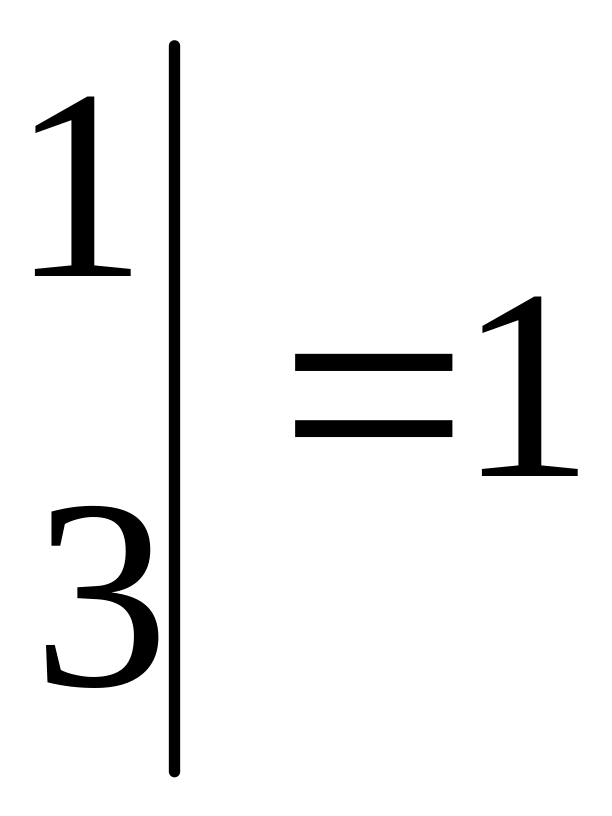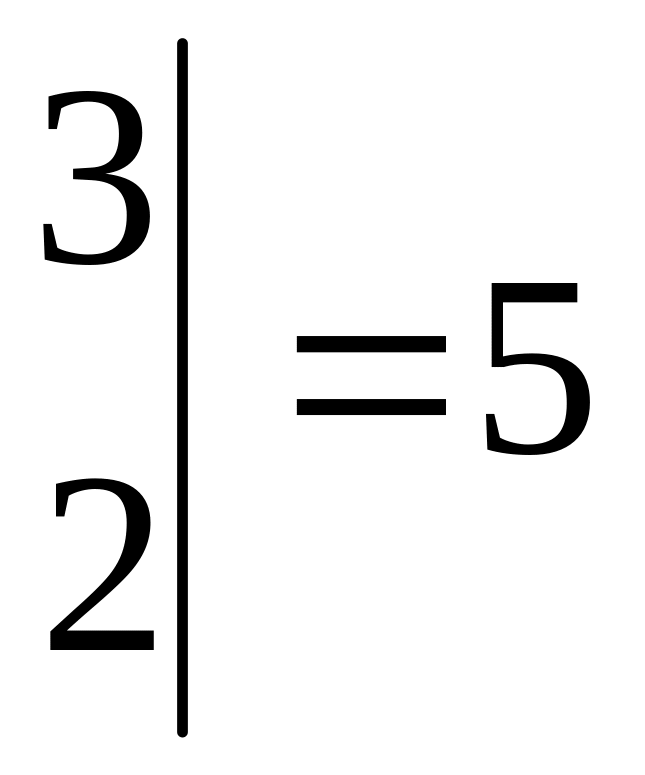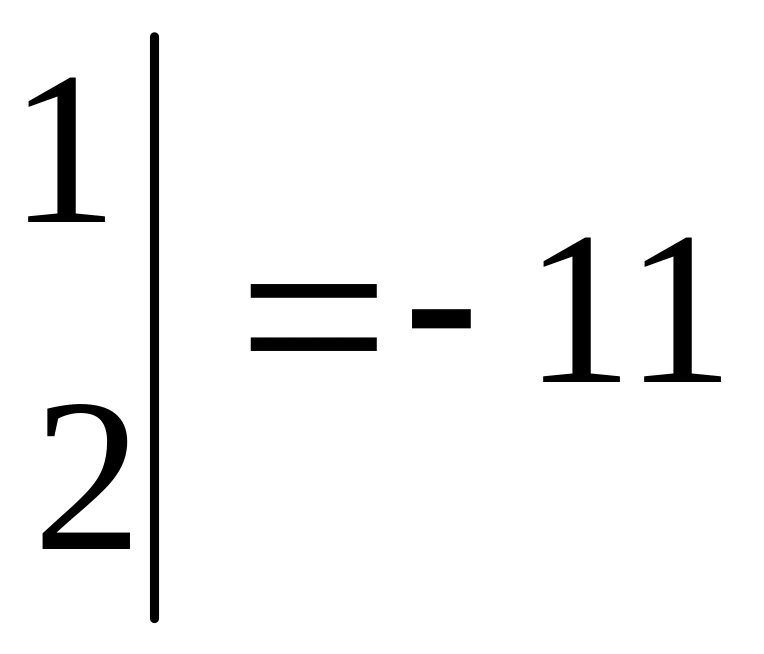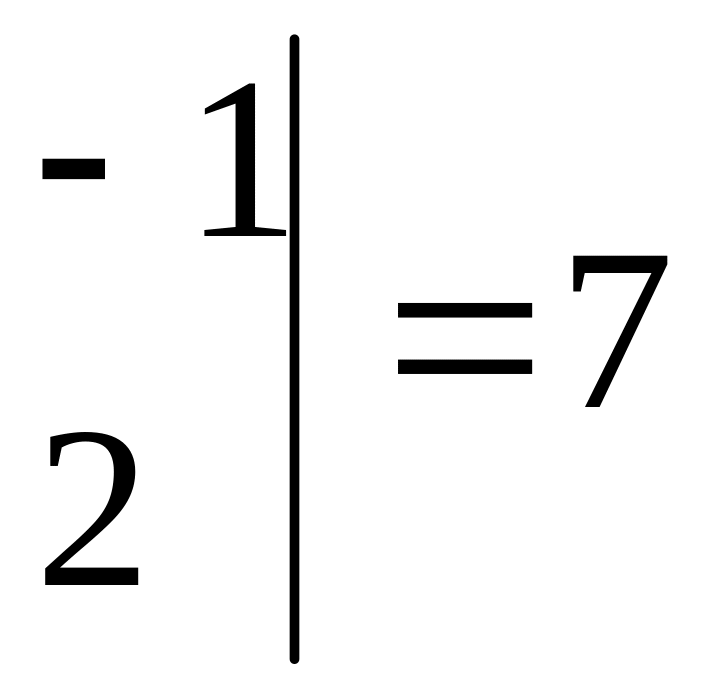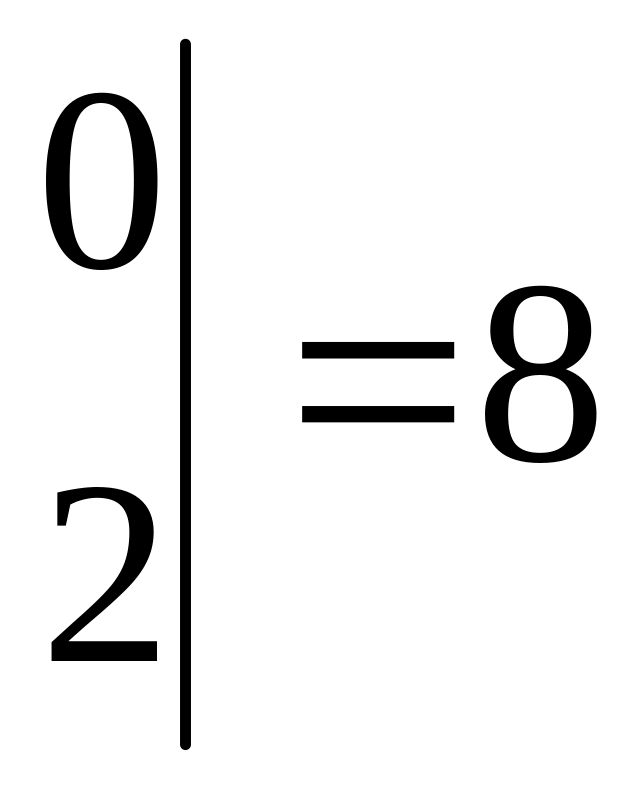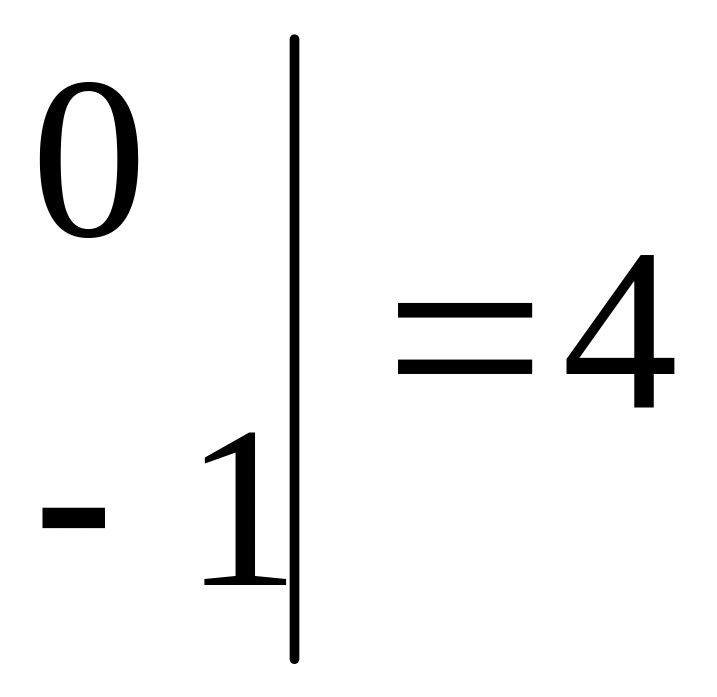Тогда

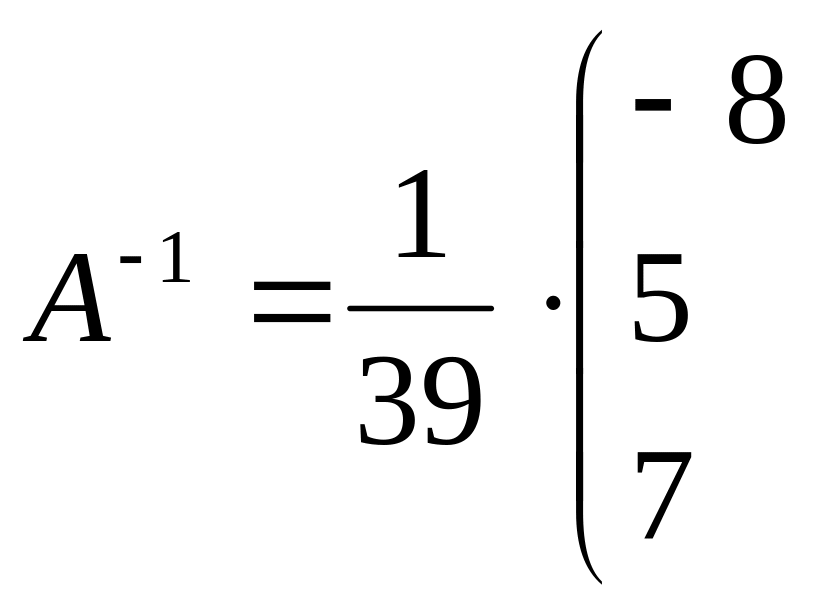
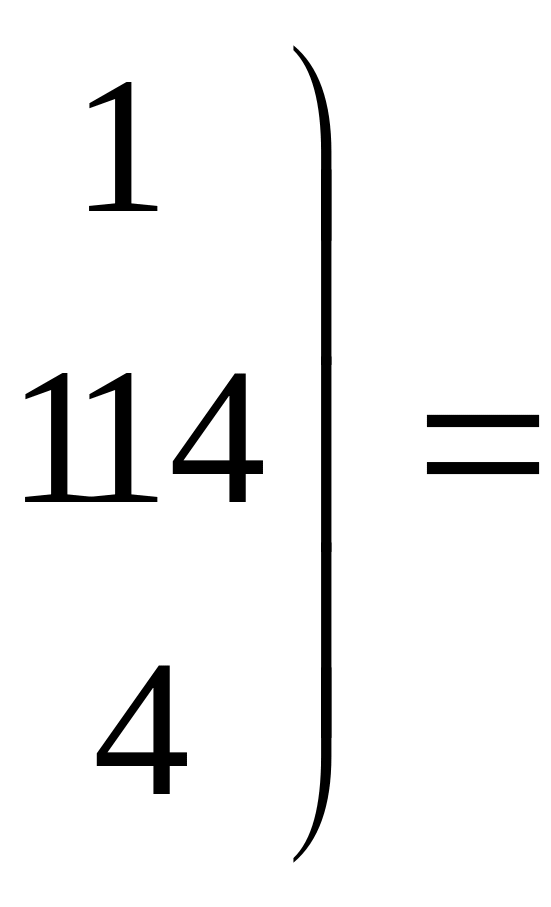
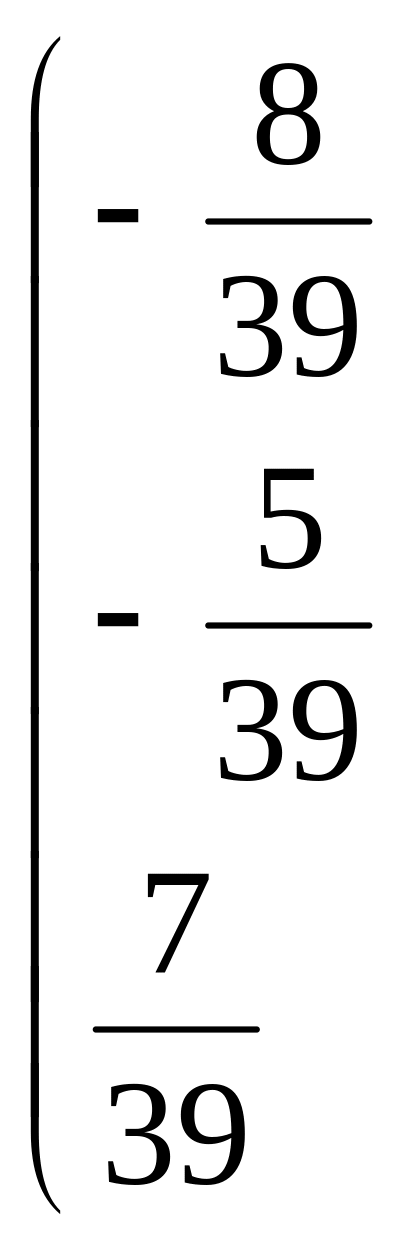
г)  Имеем:

=

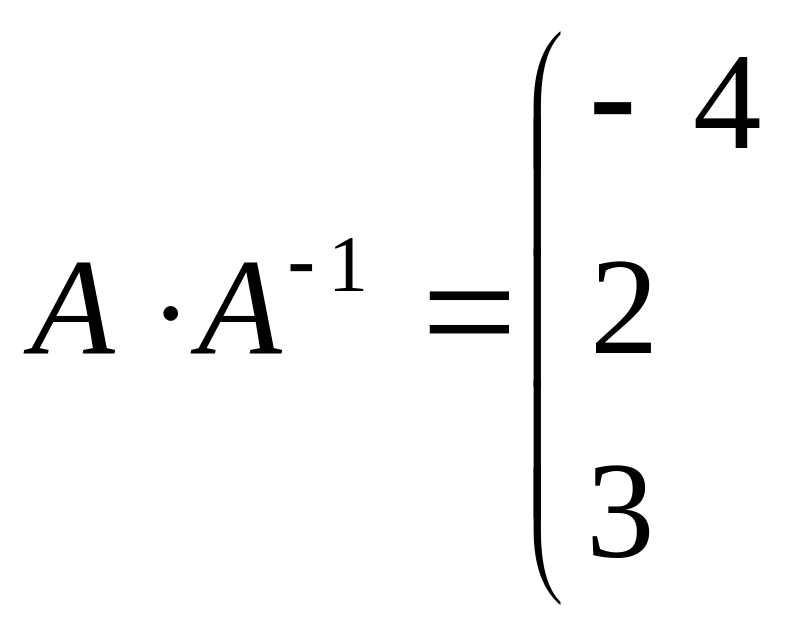
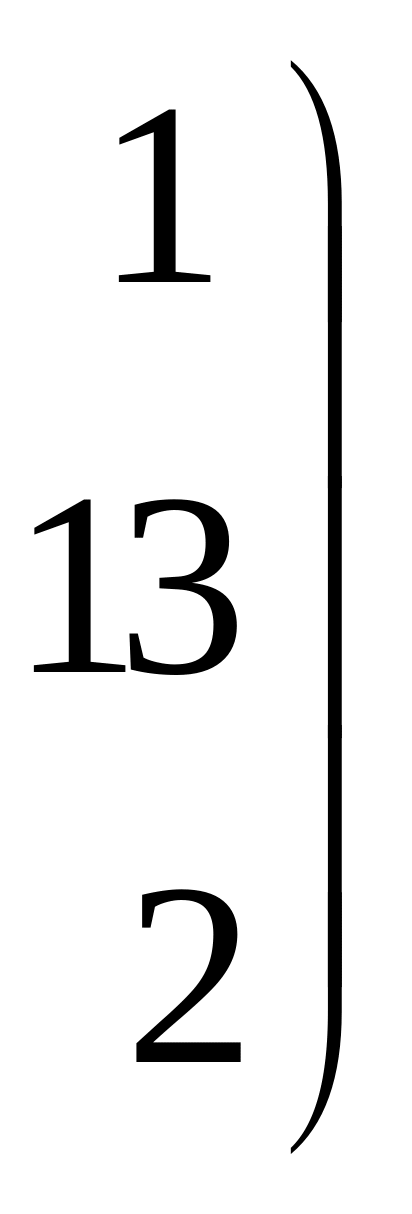
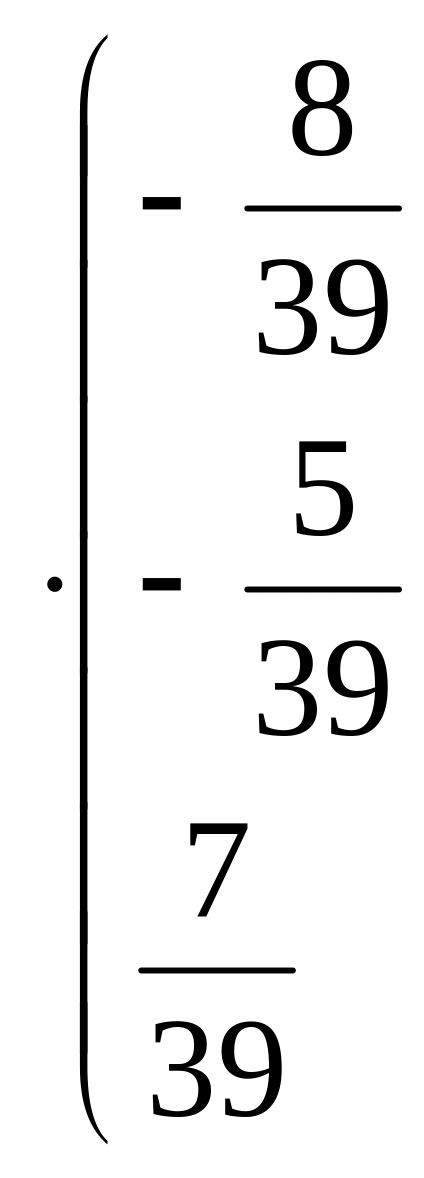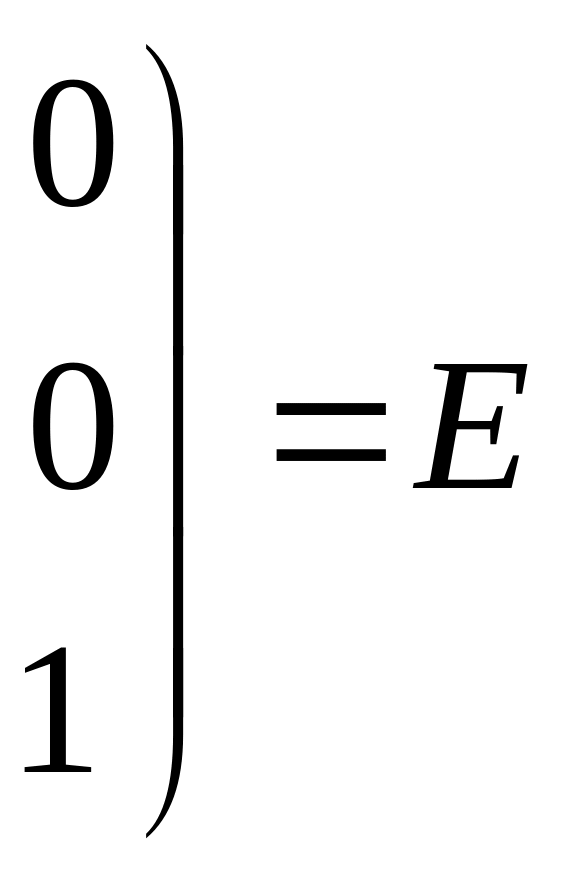
Задание 2.

Проверить совместность линейной системы уравнений и в случае совместности решить её:

а)  по формулам Крамера;

б)  методом Гауса.

Решение:

Совместность данной системы проверим по теореме Кронекера-Капелли. С помощью элементарных преобразований найдём ранг данной матрицы

и ранг расширенной матрицы .

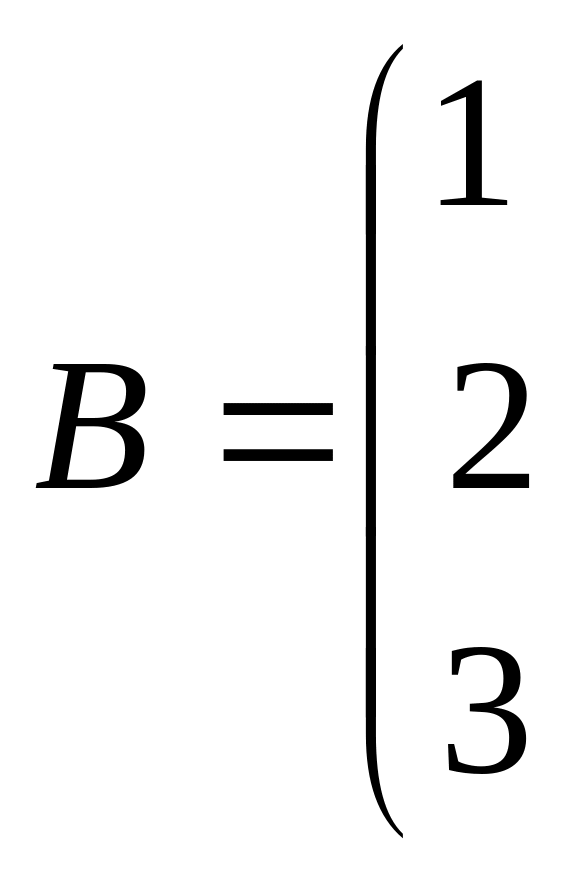
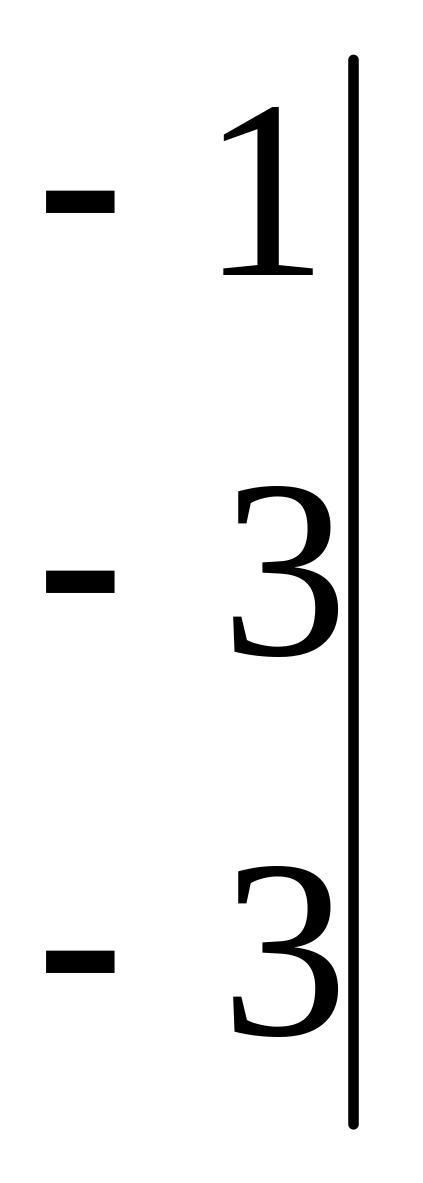
Для этого умножим первую строку матрицы на и сложим со  второй, затем умножим первую строку на и сложим с третьей, поменяем местами второй и третьи столбцы.

Получим:

~ ~ .

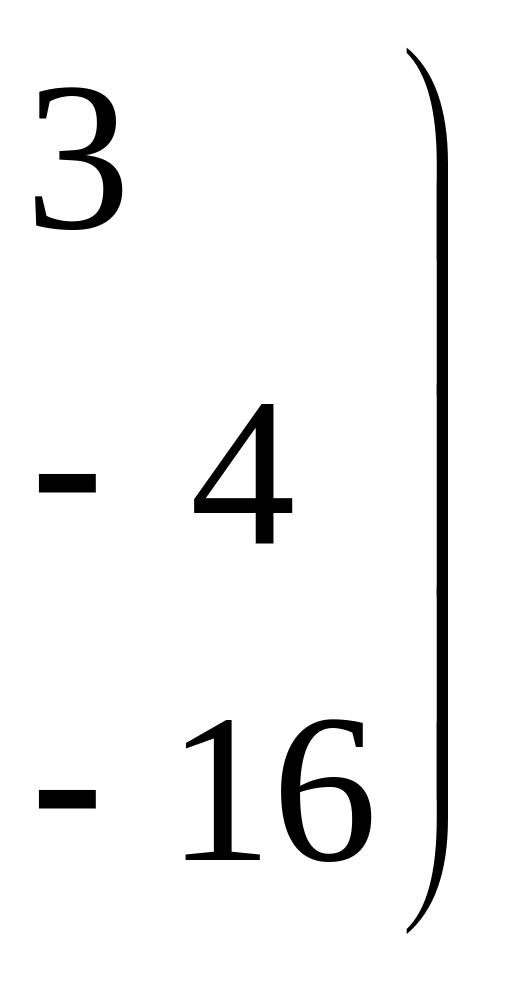Следовательно, , т.е. числу неизвестных. Значит, исходная система совместна и имеет единственное решение.

а)  по формулам Крамера

; ;

, , ,

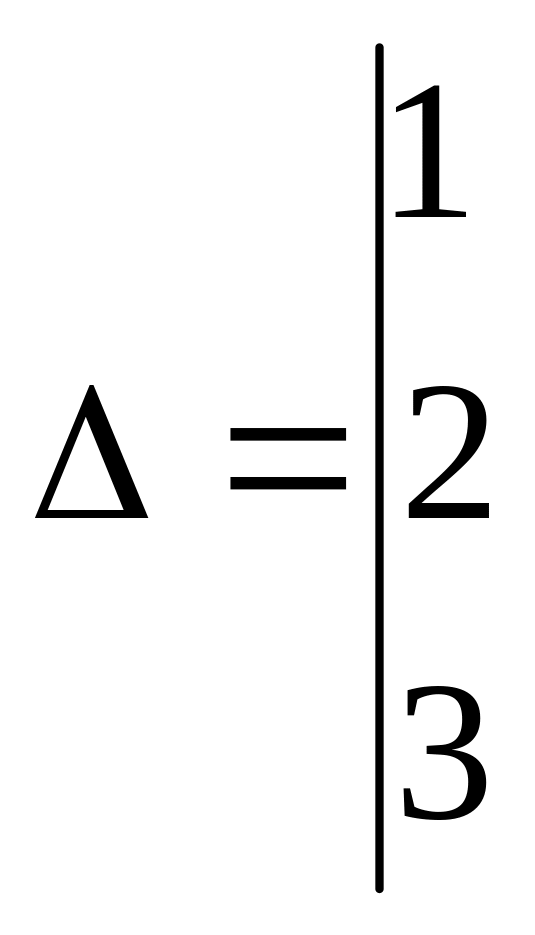
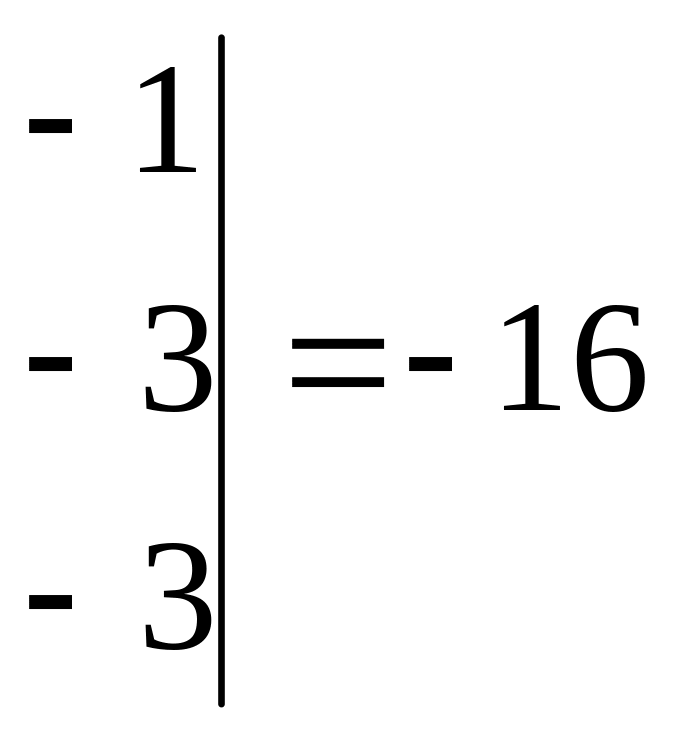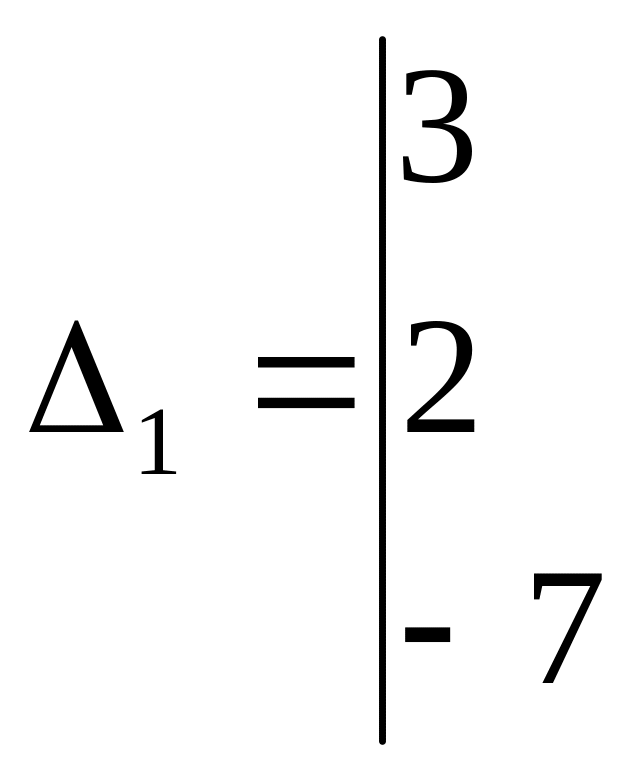
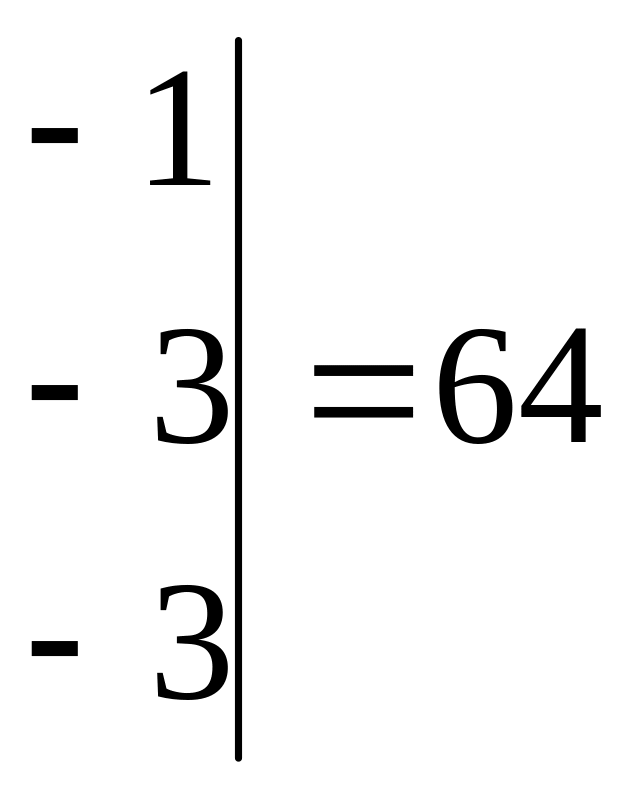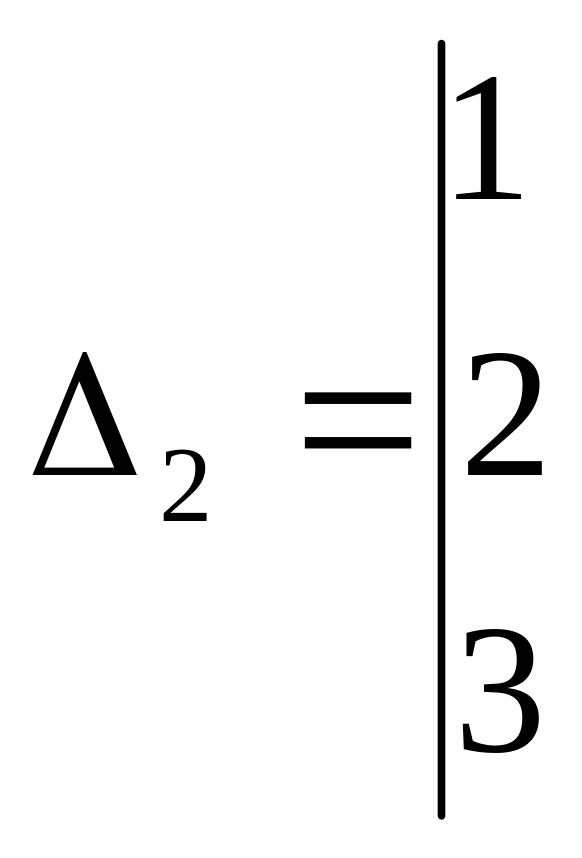
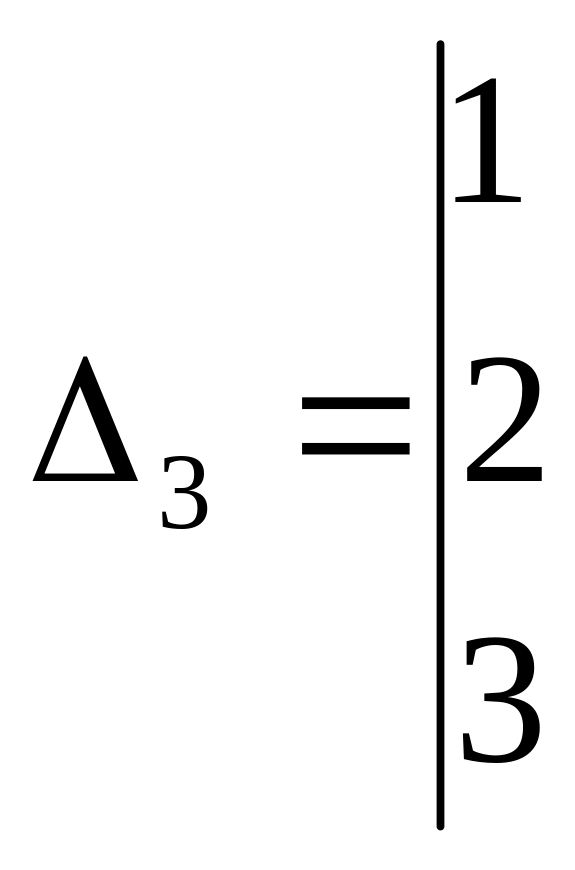
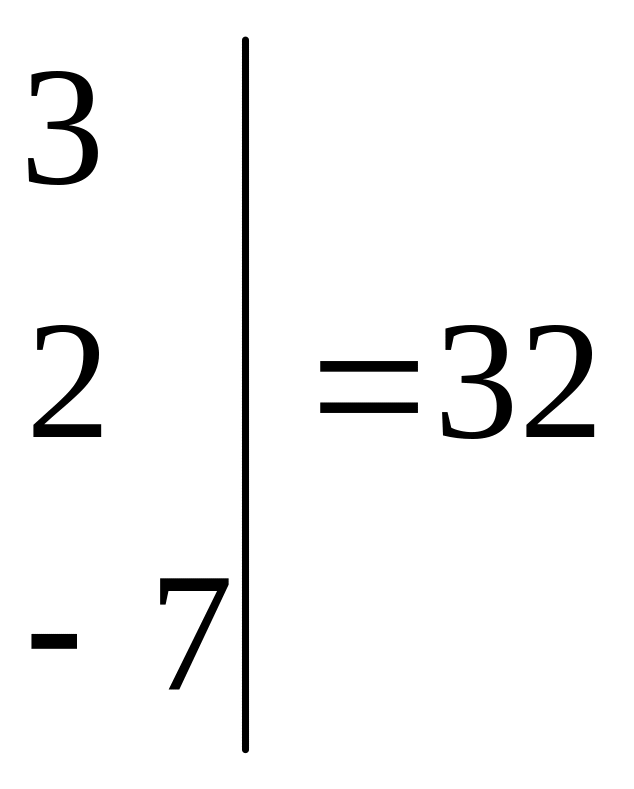, находим ; .

б)  Решим систему методом Гаусса.

Исключим из второго и третьего уравнений. Для этого первое уравнение умножим на и вычтем из второго, затем первое уравнение умножим на и вычтем из третьего:

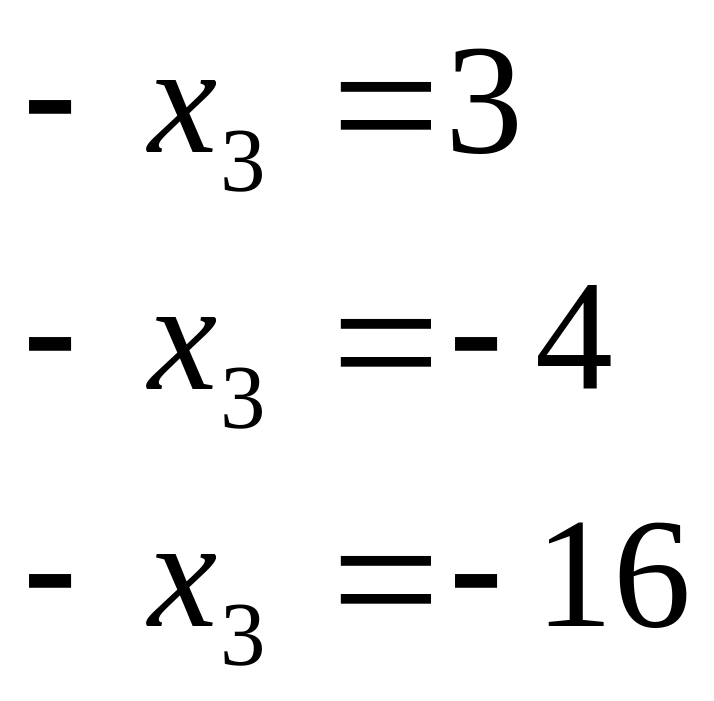
Из полученной системы находим

; ;

Задание 3.

Проверить совместность линейной системы уравнений и в случае совместности решить её:

а)  по формулам Крамера;

б)  методом Гаусса.

Решение:

Проверяем совместность системы с помощью теоремы Кронекера-Капелли. В расширенной матрице меняем третий и первый столбцы местами, умножаем первую строку на и прибавляем ко второй, умножаем первую строку на и прибавляем к третьей, из второй строки вычитаем третью:

~ ~ ~

, .

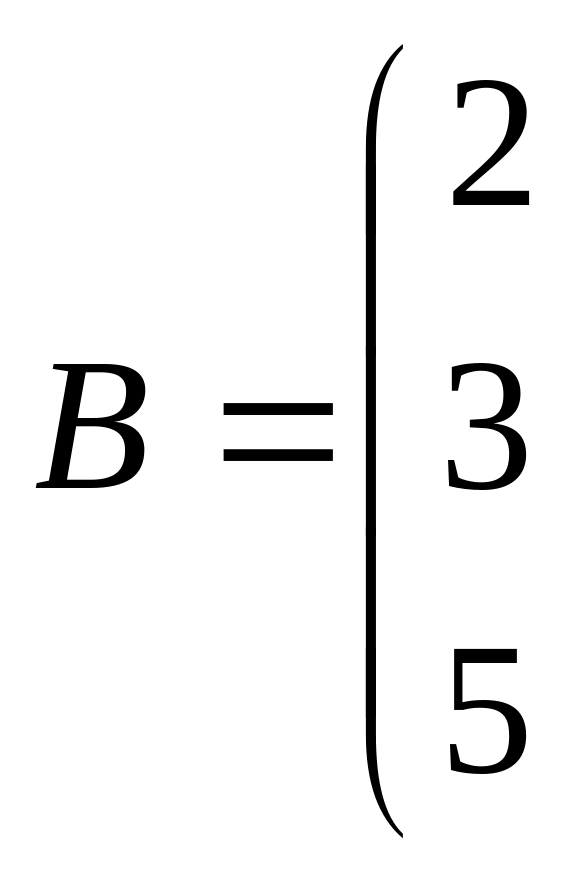
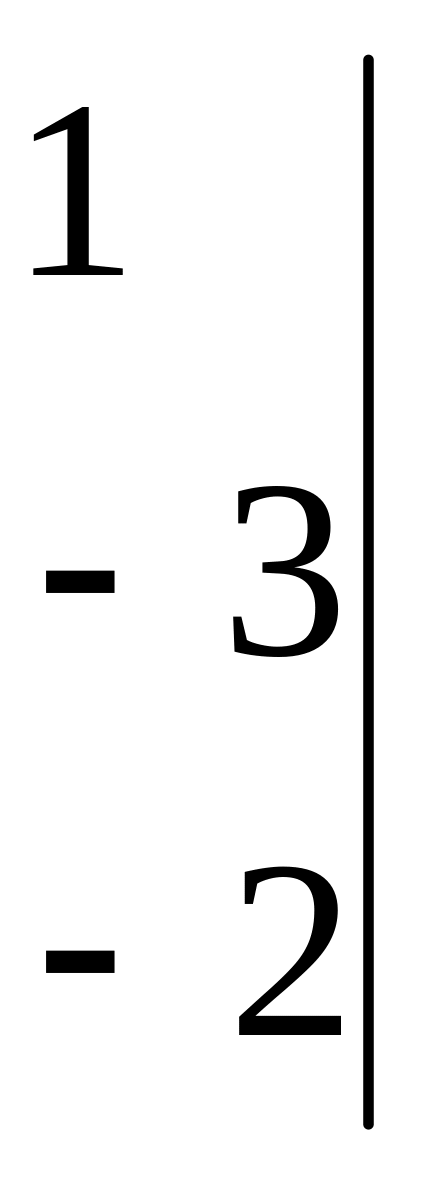
Согласно теореме Кронекера-Капелли из того, что следует несовместность исходной системы.

Задание 4.

Решить однородную систему линейных алгебраических уравнений.

Решение:

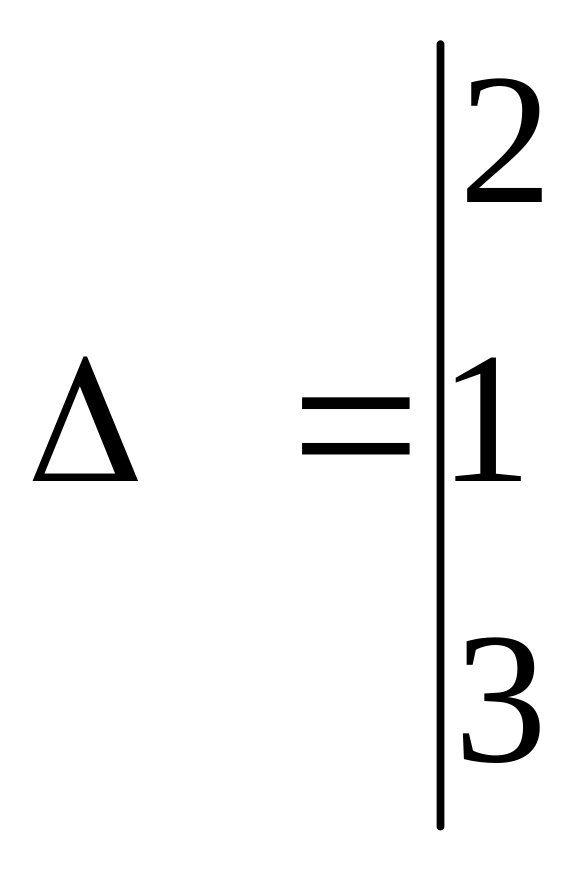
Определитель системы , поэтому система имеет единственное нулевое решение:

Задание 5.

Решить однородную систему линейных алгебраических уравнений.

Решение:

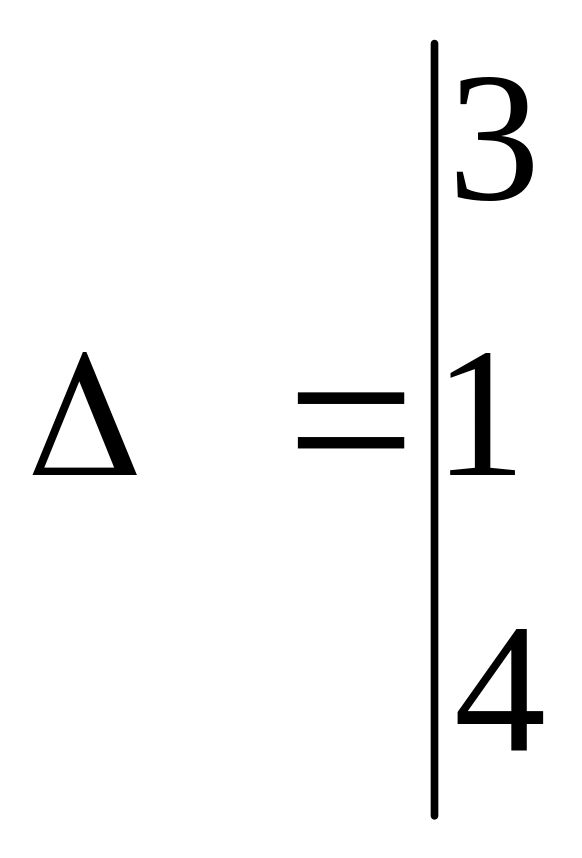
Т.к. 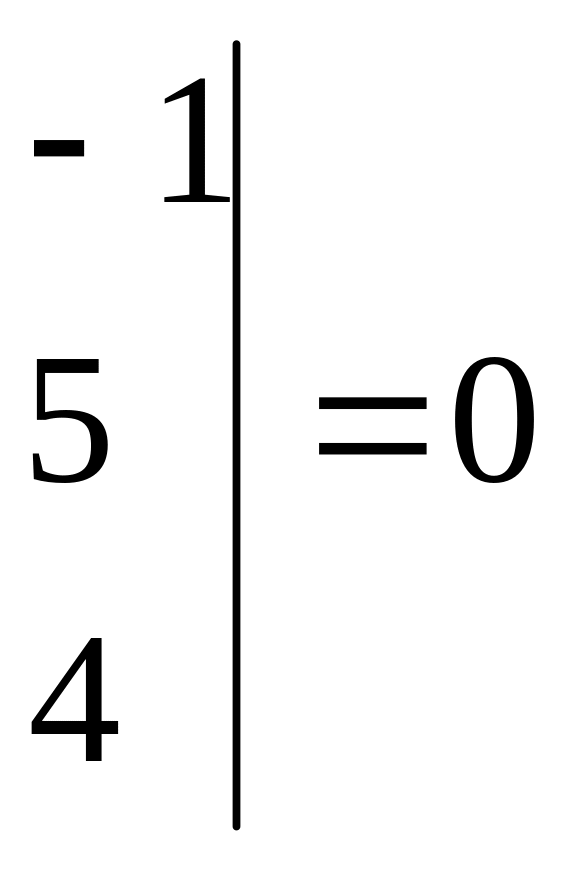, то система имеет бесчисленное множество решений. Поскольку , , возьмём любые два уравнения системы (например, 1-е и 2-е) и найдем её решение. Имеем:

Т.к. определитель из коэффициентов при неизвестных и не равен , то в качестве базисных неизвестных возьмём и (хотя можно брать и  другие пары неизвестных) и переместим члены с в  правые части уравнений:

Решаем последнюю систему по формулам Крамера:

, , .
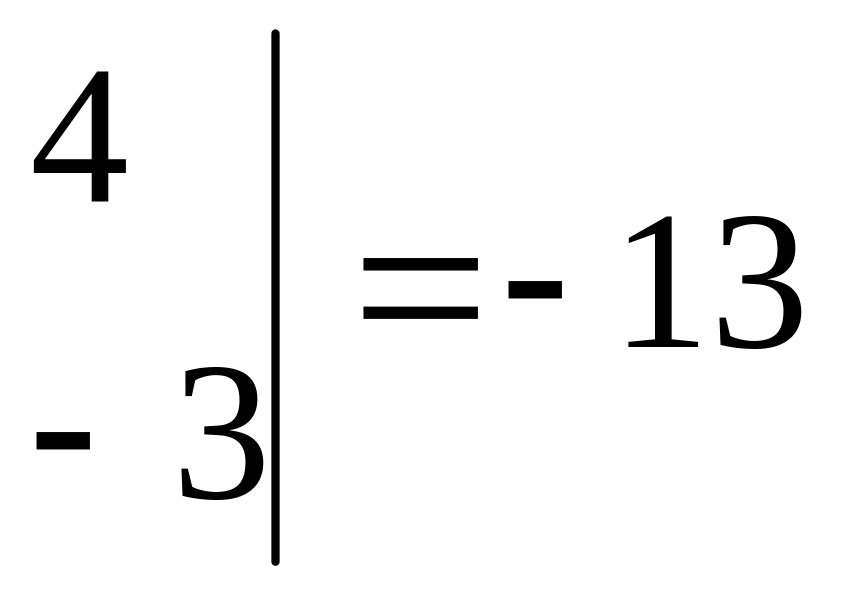
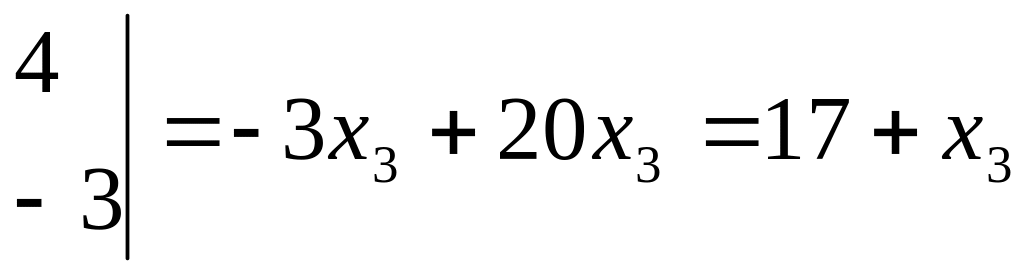
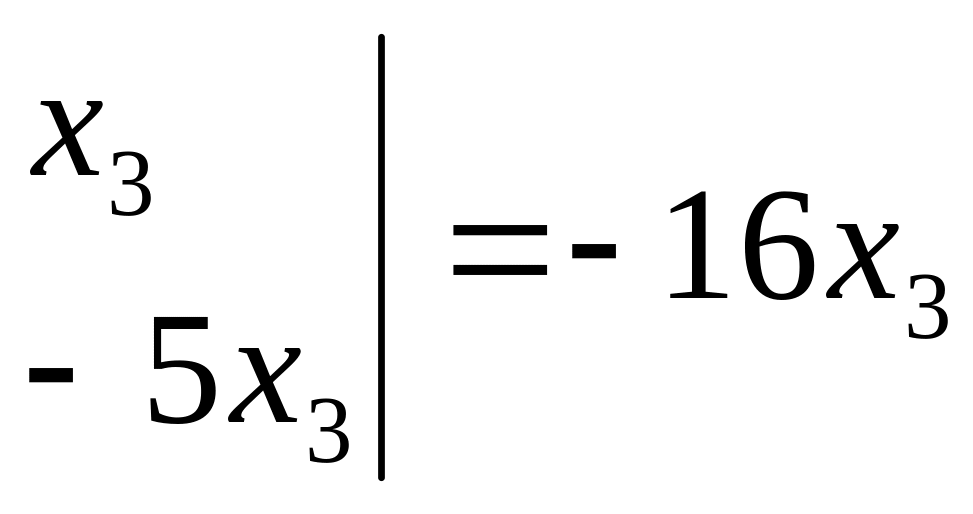