Основные теоремы дифференциального исчисления

Теорема Ролля.  Если функция непрерывна на отрезке , дифференцируема на интервале и значения функции на концах отрезка равны, , то на интервале существует точка с, , в  которой производная функции равна , .

Геометрический смысл теоремы Ролля: если условия теоремы выполняются, то на интервале существует такая точка , что в соответствующей ей точке касательная к кривой параллельна оси .

Из теоремы Ролля следует важное свойство: между двумя нулями функции находится по крайней мере один нуль ее производной.

Теорема Лагранжа.  Если функция непрерывна на отрезке и  дифференцируема на интервале , то на этом интервале найдется по  крайней мере одна точка , такая, что .

Или, что то же, если на некотором отрезке выполняются условия теоремы, то отношение приращения функции к приращению аргумента на этом отрезке равно значению производной в некоторой промежуточной точке.

Отношение равно угловому коэффициенту секущей.

Теорема Коши.  Если функции и непрерывны на отрезке , дифференцируемы на интервале и на , то существует по крайней мере одна точка , , такая, что , т.е. отношение приращений функций на данном отрезке равно отношению их  производных в точке с.

Следующая теорема, называемая правилом Лопиталя, практически облегчает задачу нахождения этого предела.

Если и дифференцируемы вблизи , непрерывны в  точке , производная функции отлична от нуля вблизи и   , то предел отношения функций при равен пределу отношения их производных, если последний (конечный или бесконечный) существует:

.

Пример 4.

Найти пределы

а)  .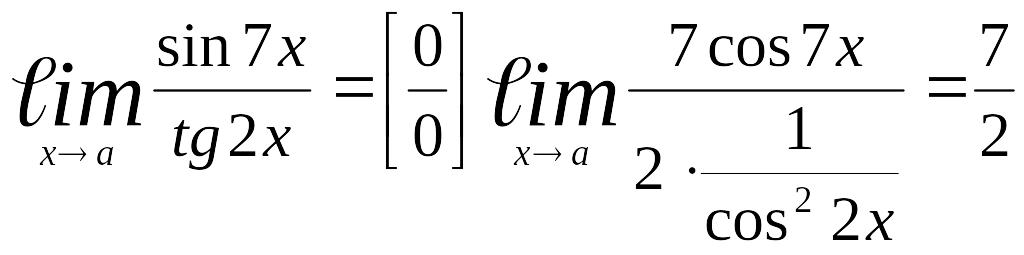

б)  .

Возрастание и убывание функций

Определение:  Функция называется возрастающей на данном промежутке, если для любых двух точек и этого промежутка из неравенства следует неравенство .

Необходимое условие возрастания и убывания дифференцируемой функции:

Если дифференцируемая функция возрастает на данном промежутке, то в любой точке этого промежутка . Если дифференцируемая функция убывает на данном промежутке, то в  любой точке этого промежутка .

Достаточное условие возрастания и убывания функции:

Пусть – дифференцируемая функция на некотором промежутке. Если в каждой точке данного промежутка , то функция возрастает на этом промежутке. Если в каждой точке данного промежутка , то функция убывает на этом промежутке.

Интервалы, на которых функция возрастает (убывает), называется интервалами монотонности функции. Точка, в которой , называется такой точкой стационарности функции .

Сформулируем правило исследования функций на возрастание и  убывание функции:

1. Находим точки из области определения функции, в которых производная функции равна нулю или не существует. Эти точки называют критическими для функции по первой производной. Критические точки разбивают область определения функции на интервалы, на каждом из которых производная 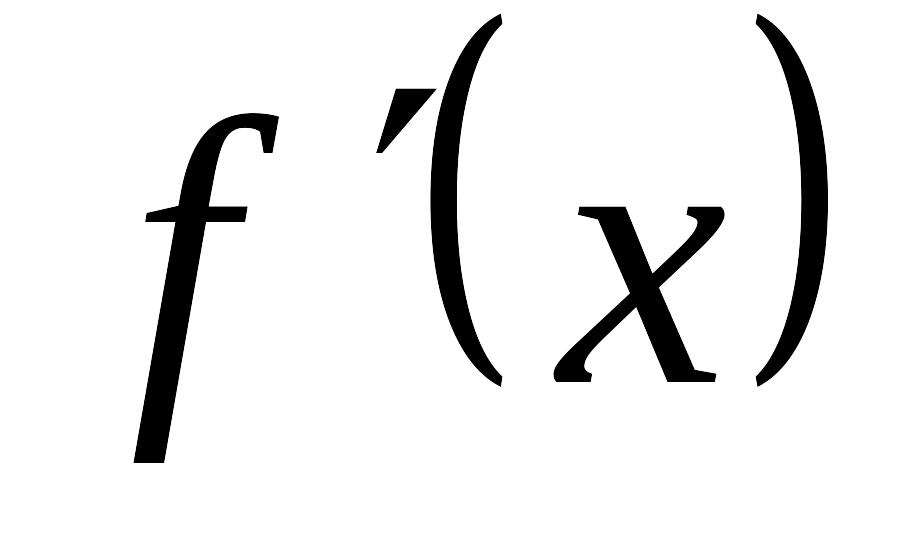сохраняет знак.

2. Исследуем знак на каждом из этих интервалов. Если на рассматриваемом интервале , то это интервал возрастания, если же , то это интервал убывания.