Тема 12. Элементы линейного программирования Общая постановка задачи
Линейное программирование – наука о методах исследования и отыскания экстремальных (наибольших и наименьших) значений линейной функции, на неизвестные которой наложены линейные ограничения.
Эта линейная функция называется целевой, а ограничения, которые математически записываются в виде уравнений или неравенств, называются системой ограничений.
Математическое выражение целевой функции и ее ограничений называется математической моделью экономической задачи.
В общем виде математическая модель задачи линейного программирования (ЛП) записывается как
при
ограничениях:
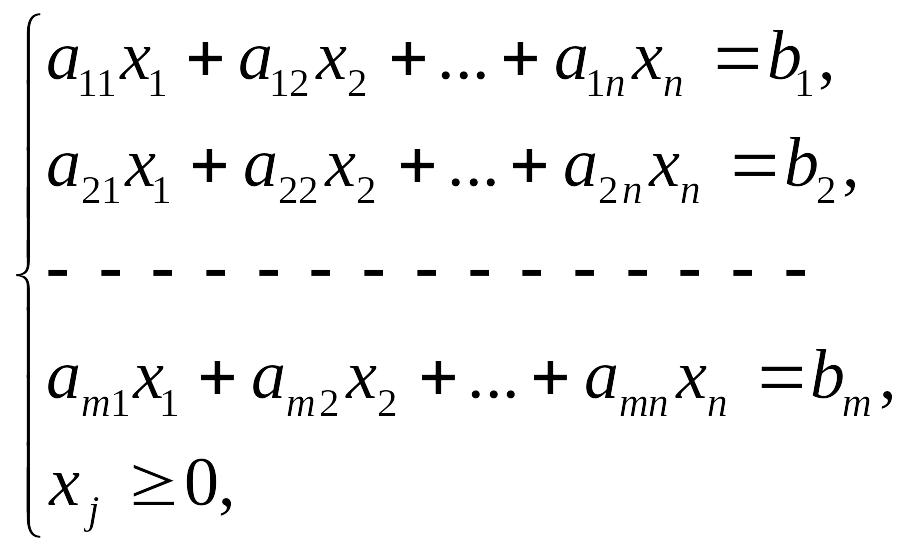
где
– неизвестные,
– заданные постоянные величины.
Все или некоторые уравнения системы ограничений могут быть записаны в виде неравенств.
Математическая
модель в более краткой записи имеет вид
при
ограничениях
Допустимым решением
задачи линейного программирования
называется вектор
,
удовлетворяющий системе ограничений.
Множество допустимых решений образует область допустимых решений (ОДР).
Допустимое решение,
при котором целевая функция достигает
своего экстремального решения, называется
оптимальным решением задачи линейного
программирования и обозначается
.
Базисное допустимое
решение
,
…,
является
опорным решением, где
– ранг системы ограничений.
Математическая модель задачи линейного программирования может быть канонической и неканонической.
Если все ограничения системы заданы уравнениями и переменные неотрицательные, то такая модель задачи называется канонической.
Если хотя бы одно
ограничение является неравенством, то
модель задачи линейного программирования
является неканонической. Чтобы перейти
от неканонической модели к канонической,
необходимо в каждое неравенство ввести
балансовую переменную
.
Если знак неравенства
,
то балансовая переменная вводится со
знаком плюс, если знак неравенства
,
то – минус. В целевую функцию балансовые
переменные не вводятся.
Чтобы составить математическую модель задачи линейного программирования, необходимо:
- ввести обозначения переменных;
- исходя из цели экономических исследований, составить целевую функцию;
- учитывая ограничения в использовании экономических показателей задачи и их количественные закономерности, записать систему ограничений.
Для рассмотрения решения задач линейного программирования применяют некоторые понятия аналитической геометрии в - мерном пространстве.
Решение систем линейных неравенств с двумя переменными
Дана система линейных неравенств с двумя переменными
Знаки некоторых или всех неравенств могут быть .
Рассмотрим первое
неравенство в системе координат
.
Построим прямую
,
которая является граничной прямой. Эта
прямая делит плоскость на две
полуплоскости 1 и 2. Для определения,
по какую сторону от граничной
прямой расположена заданная полуплоскость,
надо взять производную точку на плоскости
(лучше начало координат) и подставить
координаты этой точки в неравенство.
Если неравенство справедливо, то
полуплоскость обращена в сторону этой
точки, если не справедливо, то
в противоположную от точки сторону.
Направление полуплоскости на рисунках показываем стрелкой.
Решением каждого неравенства системы является полуплоскость, содержащая граничную прямую и расположенная по одну сторону от нее.
Пресечение
полуплоскостей, каждая из которых
определяется соответствующим неравенством
системы, называется областью решения
системы (ОР). Область решения системы,
удовлетворяющая условиям неотрицательности
называется областью неотрицательных,
или допустимых решений (ОДР).
Если система неравенств совместна, то ОР и ОДР могут быть многогранником, неограниченной многогранной областью или одной точкой.
Если система неравенств несовместна, то ОР и ОДР – пустое множество.
Пример 1. Найти ОР и ОДР системы неравенств и определить координаты угловых точек ОДР
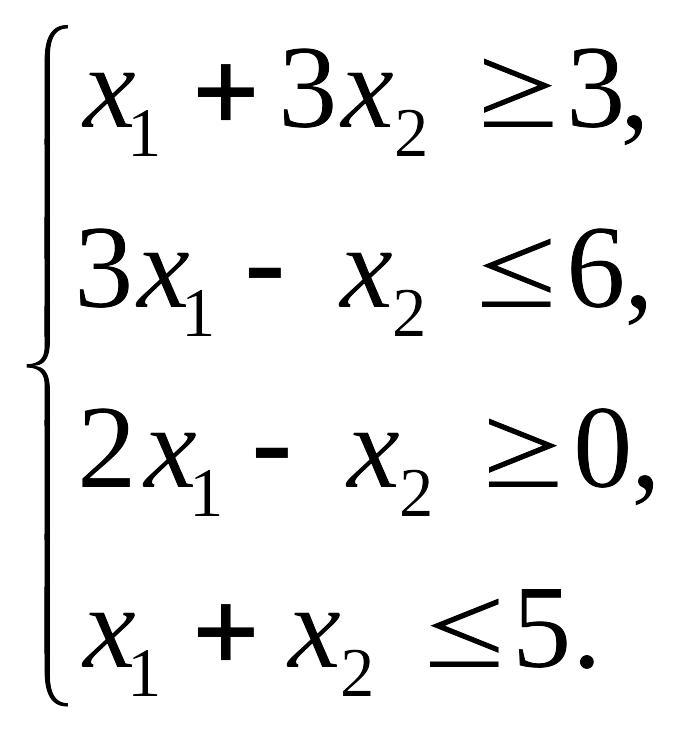
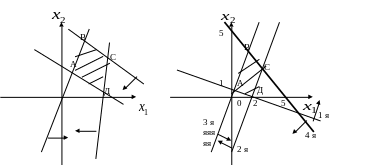
Найдем область
решений первого неравенства:
Построим координаты
точки (0;0) в неравенство:
;
так как координаты точки (0;0) не
удовлетворяют ему, то решением неравенства
является полуплоскость, не содержащая
точку (0;0).
Аналогично найдем
решения остальных неравенств системы.
Получим, что Ор и ОДР системы неравенств
является выпуклый многогранник АВСД.
Найдем угловые точки многогранника.
Точку А определим как точку пересечения
прямых
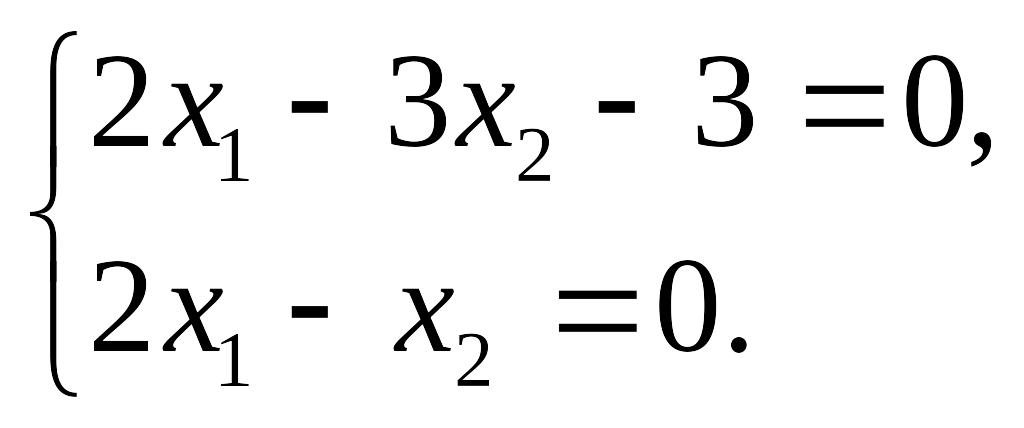
Решая систему,
получим А (
).
Точку В найдем как
точку пересечения прямых
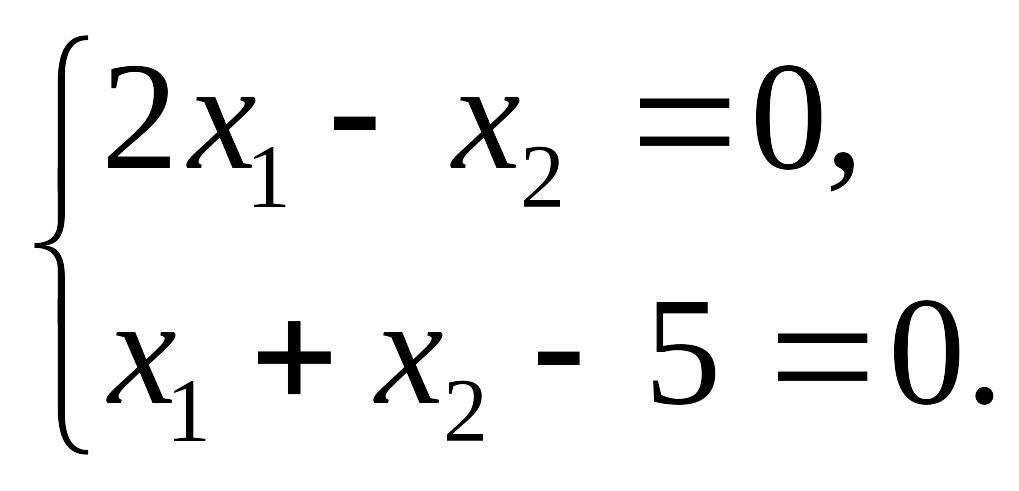
Из системы получим
В (
).
Аналогично найдем
координаты точек С и Д : С (
),
Д (
).