Вопросы для самоконтроля по теме «Неопределенный интеграл»
1. Первообразная функции. Основное свойство первообразной.
2. Неопределенный интеграл. Определение. Свойства.
3. Таблица основных неопределенных интегралов.
4. Непосредственное интегрирование.
5. Интегрирование методом подстановки.
6. Интегрирование по частям.
7. Определение правильной, неправильной рациональной дроби.
8. Виды простейших рациональных дробей.
9. Разложение правильной рациональной дроби на сумму простейших.
10. Интегрирование рациональных дробей.
11. Интегрирование выражений, содержащих радикалы.
12. Интегрирование выражений, содержащих тригонометрические функции.
Тема 7. Определенный интеграл
Пусть функция
задана на отрезке
.
Разобьем отрезок
на
– элементарных отрезков точками
.
В каждом из отрезков разбиения
выберем произвольно точку
и
положим
.
Сумма всех таких произведений
или короче:
называется интегральной суммой для
функции
на отрезке
.
Пусть существует
и конечен предел
интегральной суммы при стремлении к
нулю
,
не зависящей от способа разбиения
отрезка
на части и способа выбора точек
на отрезках разбиения. Тогда функция
называется интегрируемой на
,
число
– определенным интегралом от
на
и обозначается
;
.
Рассмотрим свойства определенного интеграла.
Свойство 1. Если нижний и верхний пределы интегрирования равны (a = b), то интеграл равен нулю:
Свойство 2. Если
f(x)
= 1, то
Свойство 3. При перестановке пределов интегрирования определенный интеграл меняет знак на противоположный:
Свойство 4. Постоянный множитель можно выносить за знак определенного интеграла:
R.
Свойство 5. Определенный интеграл от алгебраической суммы конечного числа интегрируемых на [a; b] функций f1(x), f2(x), …, fn(x) равен алгебраической сумме определенных интегралов от слагаемых:
Свойство 6. (аддитивность
определенного интеграла). Если
существует интегралы
и
то существует также интеграл
и для любых чисел a,
b,
c;
Свойство 7. Если
f(x)
≥ 0
[a;
b],
то
a
< b.
Свойство 8. (определенность определенного интеграла). Если интегрируемые функции f (x) и φ (x) удовлетворяют неравенству f (x) ≥ φ (x) [a; b], то
a
>b.
Свойство 9. (об
оценке определенного интеграла). Если
m
и М – соответственно наименьшее и
наибольшее значения функции f (x),
непрерывной на отрезке [a;
b],
то
a
< b.
Свойство 10. (теорема
о среднем). Если
функция f (x)
непрерывна на отрезке [a;
b],
то существует такая точка
[a;
b],
что
т.е. определенный
интеграл от переменной функции равен
произведению значения подынтегральной
функции в некоторой промежуточной точке
ξ отрезка интегрирования [a;
b]
и длины b
– a
этого отрезка.
Формула Ньютона-Лейбница
Формула Ньютона-Лейбница дает правило вычисления определенного интеграла: значение определенного интеграла на отрезке [a; b] от непрерывной функции f (x) равно разности значений любой ее первообразной, вычисленной при x = b и x = a.
Определенный
интеграл от непрерывной на
функции
равен приращению любой ее первообразной
на этом отрезке:
,
или
Формула Ньютона-Лейбница дает простой и удобный метод вычисления определенных интегралов от непрерывных функций, применимый в тех случаях, когда первообразная подинтегральной функции может быть найдена в элементарных функциях.
Пример 1.
Вычислить интегралы
.
Пример 2.
.
Пример 3.
.
Пример 4.
.
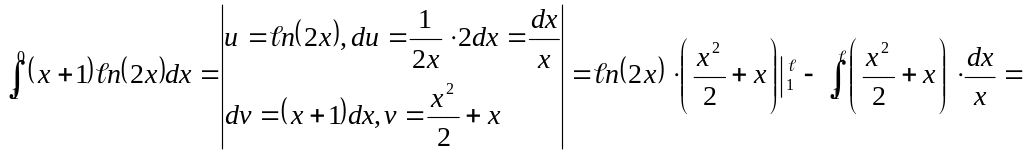
Приложения определенного интеграла
Вычисление площадей плоских фигур:
Площадь криволинейной трапеции, ограниченной кривой y = f (x) [f(x) ≥ 0], прямыми x = a и x = b и отрезками [a; b] оси Ох, вычисляется по формуле:
Площадь фигуры, ограниченной кривыми y = f1(x) и y = f2(x)[f1(x) ≤ f2(x)] и прямыми x = a и x = b, находится по формуле:
Если кривая задана параметрическими уравнениями x = x (t), y = y (t), то площадь криволинейной трапеции, ограниченной этой кривой, прямыми x = a, x = b и отрезком [a; b] оси Ох, выражается формулой:
где t1 и t2 определяются из уравнений a = x(t1), b = x(t2) [y(t) ≥ 0 при t1 ≤ t ≤ t2].
Определение и вычисление длины кривой:
Если кривая y = f (x) на отрезке [a; b] – гладкая (т.е. производная y’ = f’(x) непрерывна), то длина соответствующей дуги этой кривой находится по формуле:
При параметрическом задании кривой x = x (t), y = y (t) [x(t) и y(t) – непрерывно дифференцируемые функции] длина дуги кривой, соответствующая монотонному изменению параметра t от t1 до t2, вычисляется по формуле:
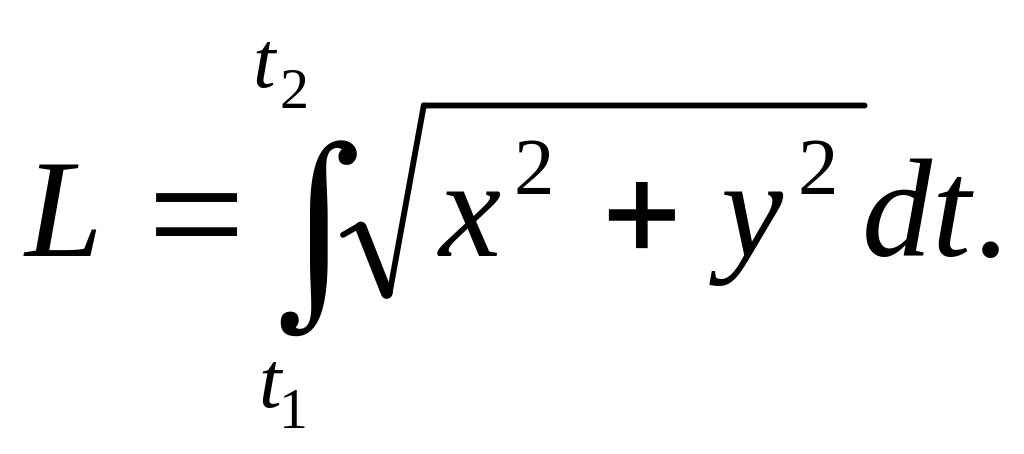
Дифференциал длины дуги:
Длина дуги кривой определяется формулой:
где y = f (x) [a; b]. Предположим, что в этой формуле нижний передел интегрирования остается постоянным, а верхний изменяется. Обозначим верхний предел буквой х, а переменную интегрирования буквой t. Длина дуги будет функцией верхнего предела:
Объем тела вращения
Если необходимо определить объем тела Vх, образованного вращением вокруг оси Ох криволинейной трапеции y = f (x) (f(x) ³ 0), отрезок a £ x £ b, то следует воспользоваться формулой:
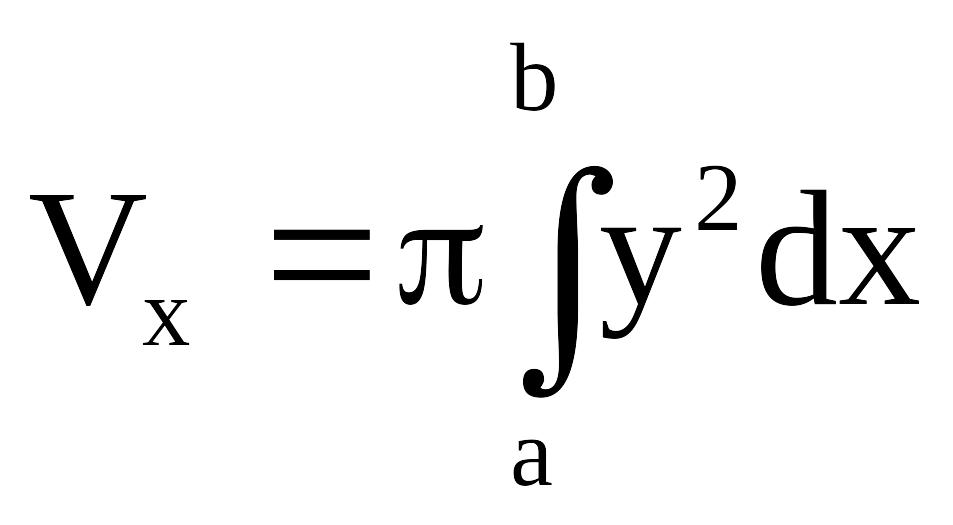
Пусть теперь необходимо определить объем тела Vу, образованного вращением вокруг оси Оу криволинейной трапеции x = g (y) ³ 0, y = c, y = d. Тогда
.
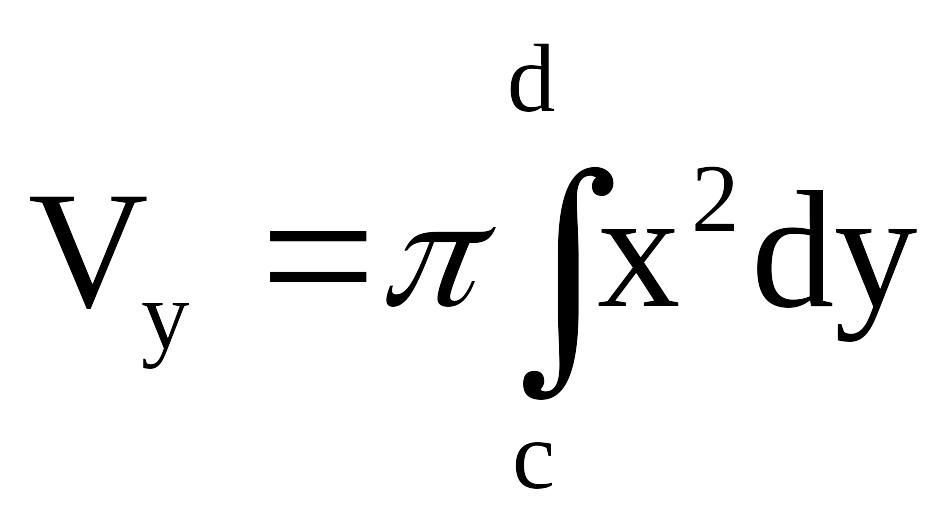Вопросы для самоконтроля по теме
«Определенный интеграл»
1. Определение определенного интеграла и его геометрический смысл.
2. Вычисление определенного интеграла по формуле Ньютона-Лейбница.
3. Свойства определенного интеграла.
4. Нахождение площади криволинейной трапеции.
5. Нахождение объемов тел вращения с помощью определенного интеграла.
6. Метод подстановки при вычислении определенного интеграла.
7. Вычисление определенного интеграла методом интегрирования по частям.
8. Длина дуги кривой.
9. Площадь поверхности вращения.