Определители третьего порядка

Рассмотрим таблицу (матрицу) из девяти чисел (элементов матрицы):

(1)

Определение:  Определителем третьего порядка, соответствующим матрице (1), называется число , равное следующей алгебраической сумме произведений элементов матрицы:

.

Закон составления оказывается весьма простым, если воспользоваться правилом, которое называется правилом треугольников  или правилом Саррюса.

Пример 1.

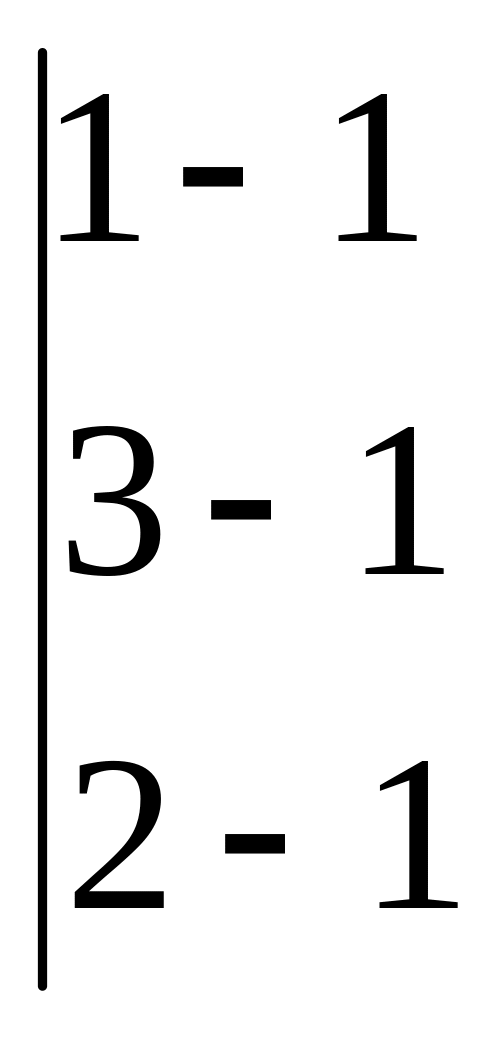
Рассмотрим матрицу и соответствующий ей определитель

Определение:  Минором любого элемента этого определителя называется определитель второго порядка, соответствующий матрице, полученной из данной вычеркиванием строки и столбца, в которых лежит  указанный элемент.

Минором элемента является определитель .

Определение:  Алгебраическим дополнением любого элемента определителя называют минор этого элемента, взятый со знаком , где – номер строки, – номер столбца определителя , в  которых лежит данный элемент.

Обозначают алгебраическое дополнение элемента обычно большой буквой того же наименования и с тем же номером (индексом), что и  у  данного элемента. Например, алгебраическое дополнение элемента обозначают , и т.д.

Таким образом, по определению ; и т.д.

Теорема.  Определитель равен сумме произведений элементов любого его столбца или строки на их алгебраические дополнения.

Другими словами, имеют место следующие равенства:

Запись по любой из указанных формул называется разложением этого определителя по элементам соответствующего столбца или строки. Эти разложения удобно использовать для вычисления определителей третьего порядка. Для определителей третьего порядка справедливы все свойства 1–7, рассмотренные выше для определителей второго порядка.

Применение определителей к решению систем линейных уравнений

Рассмотрим систему двух уравнений первой степени (линейных уравнений) с неизвестными и :

(1)

Числа , , , называют коэффициентами, а числа , – свободными членами. В случае, если , система (1) называется однородной системой линейных уравнений, в противном случае, т.е. если хотя бы одно из чисел и отлично от нуля, – неоднородной.

Решением системы (1) является всякая пара чисел , , обращающая оба уравнения системы в тождества.

Назовем главным определителем , определитель составленный из   коэффициентов при неизвестных , назовем вспомогательными определителями. Если , то система имеет единственное решение. Его можно найти по формулам ; , называемым формулами Крамера.

Пусть , при этом оба определителя и также равны , то в  этом случае система имеет бесчисленное множество решений.

.

Если же , но среди определителей и хотя бы один не  равен   , то система решений не имеет.

Пример 2.  Решить системы уравнений

Найдём . Система имеет единственное решение

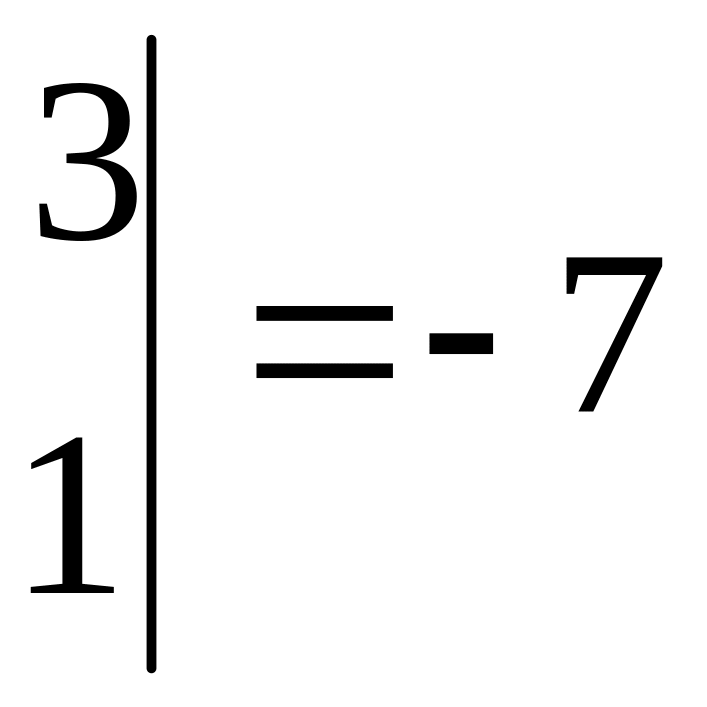
По формулам Крамера получаем , .

Пример 3.  

, ,

Система имеет бесчисленное множество решений. Решения этой системы – пары чисел , , где – любое число.

Пример 4.

Система решений не имеет, т.к. , .

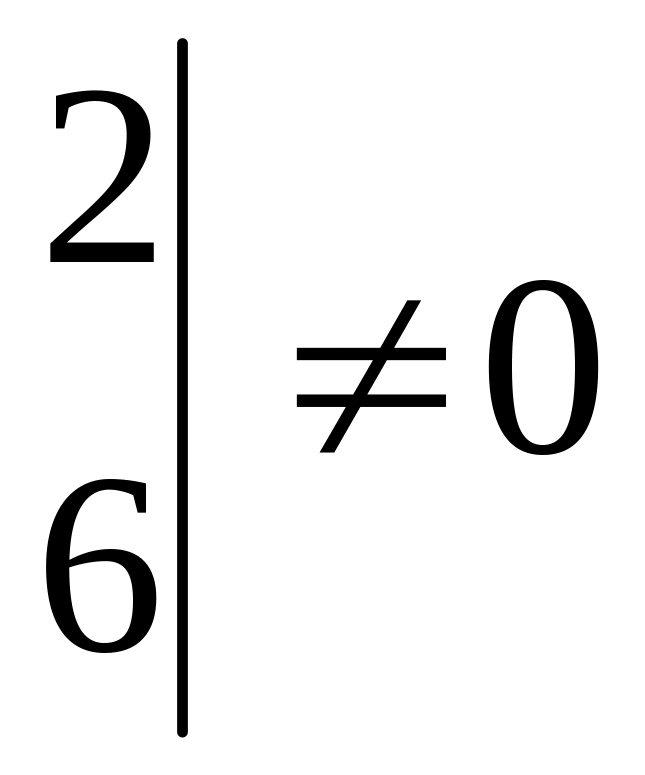Пусть дана система трех уравнений первой системы с  неизвестными , , :

Числа при неизвестных назовем коэффициентами системы, а  числа , , – свободными членами.

Решением системы является всякая тройка чисел , , , обращающая уравнения системы в тождества. Система, имеющая решение, называется совместной.

Если , то система имеет единственное решение. Его можно найти по  формулам Крамера: , ,

Здесь – определитель системы

, , – определители, полученные из заменой в нём соответственно первого, второго и третьего столбцов столбцом свободных  членов данной системы.

Пример 5.  Решите систему уравнений

Вычислим

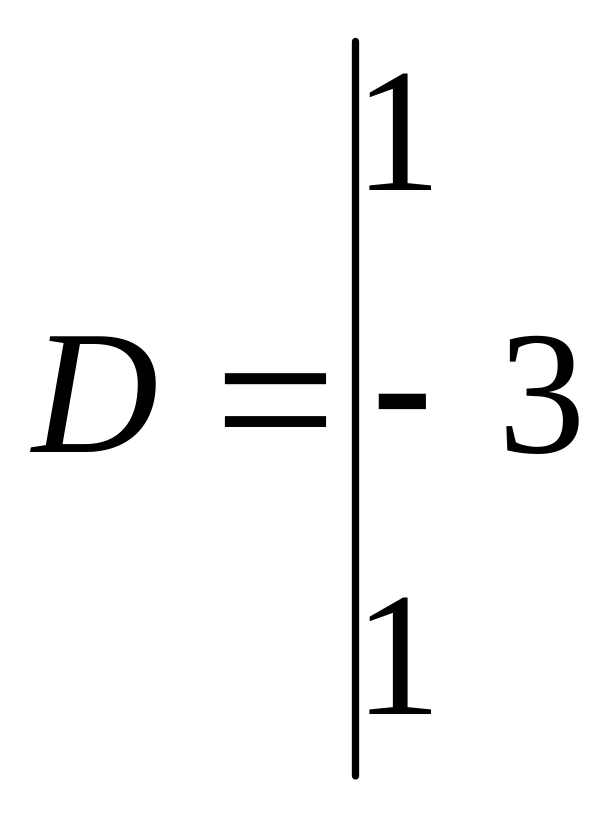
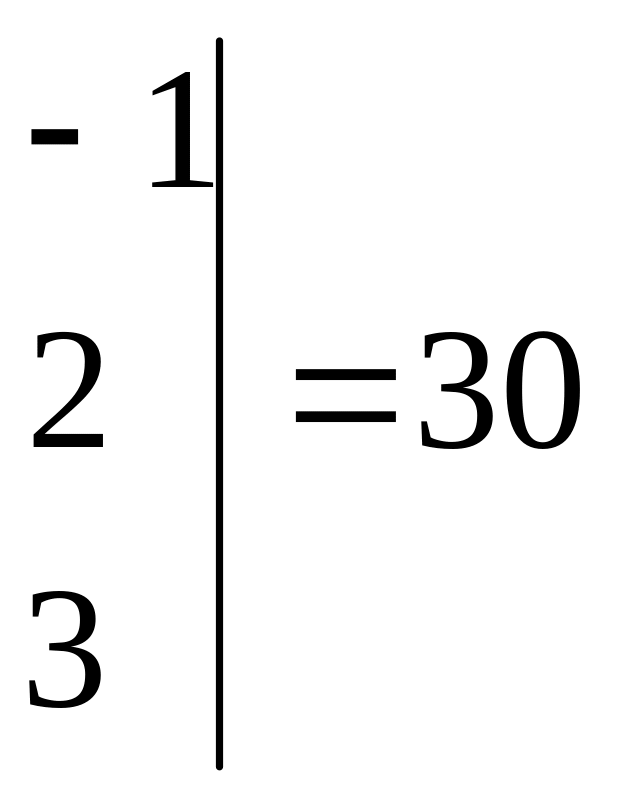
Т.к. , система имеет единственное решение.

Найдём его по формулам Крамера:

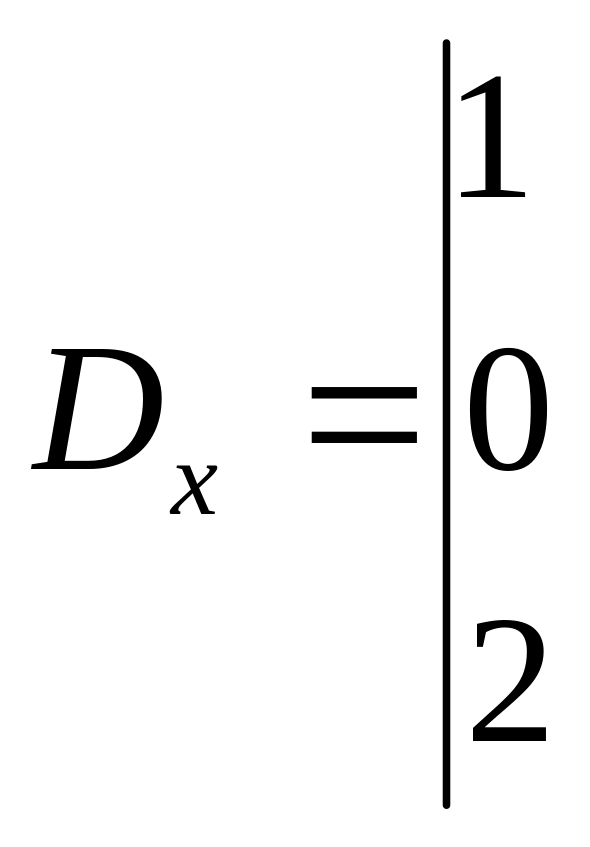
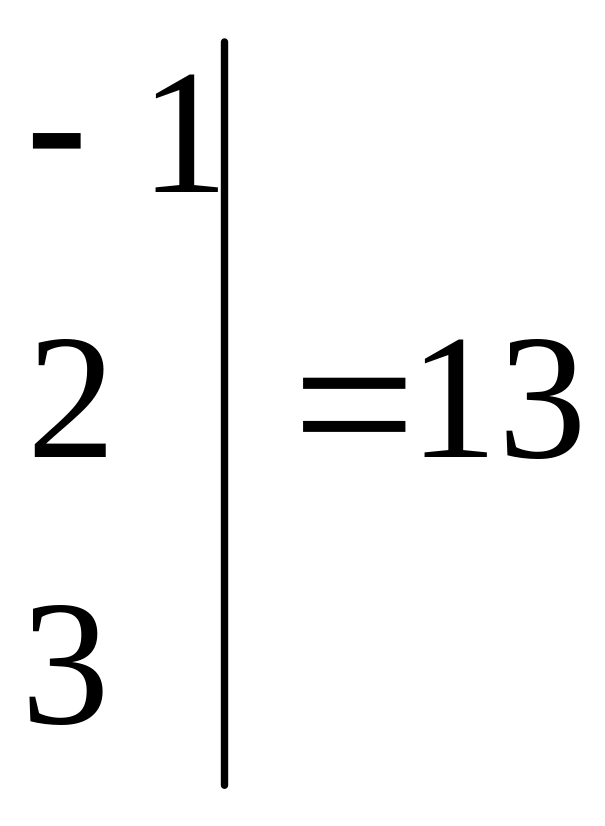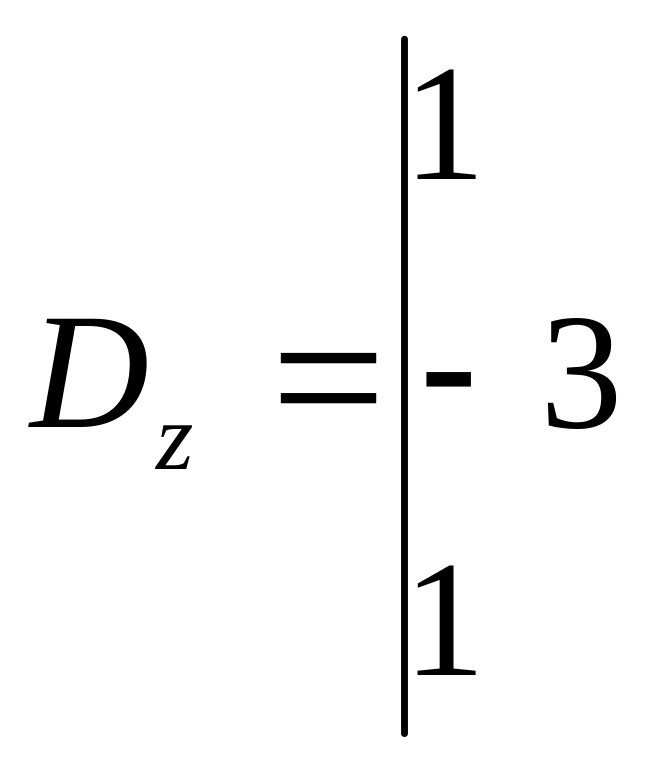
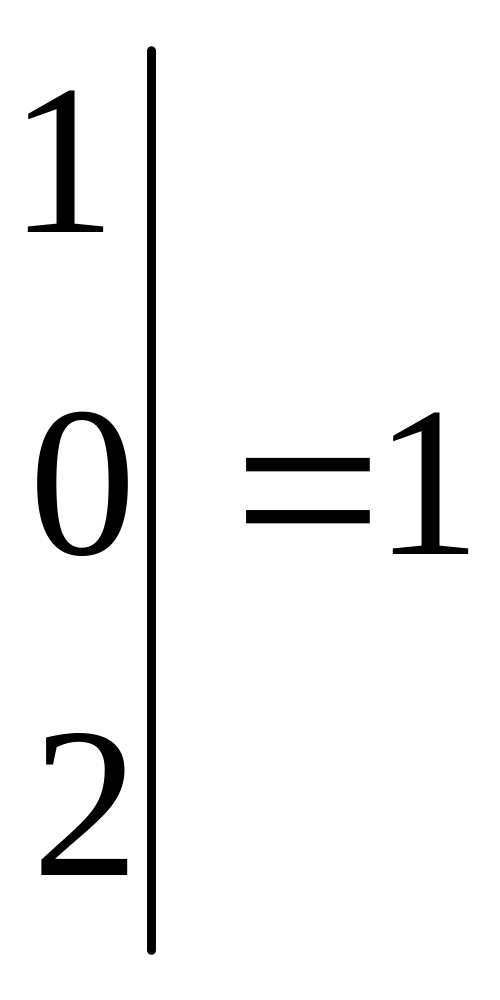, , , следовательно

, ,

Пример 6.  Решите систему уравнений (самостоятельно)

Система несовместна, т.к. ,

Пример 7.  Решите систему уравнений (самостоятельно)

Система имеет бесчисленное множество решений