Предел функции

Пусть функция определена в некоторой окрестности точки , т.е.  в  некотором интервале, содержащем , кроме, быть может, самой точки . В точке функция может быть и не определена.

Определение:  Число называется пределом функции при , стремящемся к (или в точке ), если для любого положительного числа найдется такое положительное число , что для всех , удовлетворяющих условию выполняется неравенство .

Из определения следует, что для любого > 0 (положительное число может быть сколь угодно малым) существует такое, что для всех точек симметричного относительно интервала , , , значения функции не выходят из – окрестности точки .

Тот факт, что предел функции при равен , записывают так: или при

0

На следующем рисунке функция не имеет предела при

Пример 3. Докажем, а что функция при имеет предел, равный 5.

Для доказательства установим, что какое бы положительное число   мы не взяли, можно найти такое положительное число , что для всех значений , отличающихся по абсолютной величине от числа меньше чем на , будет справедливо неравенство . Отсюда . Поэтому, если взять , удовлетворяющее условию , то будет отличаться от числа по абсолютной величине меньше на при . А это означает, что .

Определим предел функции при стремлении аргумента к  бесконечности.

Определение: Число называется пределом функции при , если для любого > 0 найдется такая окрестность символа , что все значения функции в точках этой окрестности отличаются от числа по  абсолютной величине меньше чем на .

Если , то график функции асимптотически приближается к  прямой при стремлении к бесконечности как по  положительным, так и по отрицательным значениям (смотри рисунок).

Основные теоремы о пределах функции

Пусть – число или один из символов ; ; .

Теорема 1.  Предел постоянного равен этому постоянному: .

Если и при имеют конечные пределы, то справедливы следующие теоремы:

Теорема 2.   .

Теорема 3.   .

Теорема 4.   при условии .

Рассмотрим некоторые замечательные пределы.

Пусть ,

( , ).

Тогда

Пример 4.

Пример 5.

называют первым замечательным пределом.

Пример 6.

называют вторым замечательным пределом.

Если в этом равенстве положить ( , то ), то оно запишется в виде .

Пример 7.

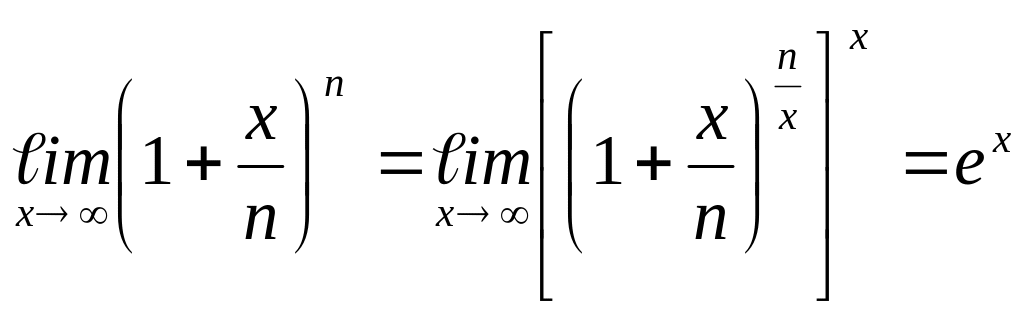
Пример 8. Найти

Преобразуем выражение в скобках, выполнив деление «уголком» числителя на знаменатель. Получаем . Пусть , тогда и , причем при имеем . Следовательно, .