Тема 3. Введение в анализ Последовательность, предел последовательности

Одним из основных понятий математического анализа является понятие функции.

Определение:  Переменная называется функцией от другой переменной , если каждому значению из некоторого множества по определенному правилу или закону ставится в соответствие одно или несколько значений переменной .

Если по некоторому закону каждому натуральному числу поставлено в  соответствие определенное число , то говорят, что задана числовая последовательность или функция натурального аргумента. Общий член последовательности является функцией натурального аргумента , . Давая различные значения: , , ,…, получим последовательность значений этой функции: , , …, .

Функцию можно задать как аналитически, так и любым другим способом.

Определение:  Число называется пределом последовательности , если для любого положительного числа найдется такой номер , выполняется неравенство .

Геометрически определение предела последовательности можно сформулировать следующим образом: число является пределом последовательности , если какова бы ни была – окрестность точки , начиная с некоторого номера все точки попадут в эту окрестность, т.е.  вне интервала ) останется лишь конечное число членов последовательности.

Тот факт, что последовательность имеет предел, равный , записывают: . Говорят, что последовательность сходится или имеет конечный предел.

Определение:  Последовательность называется бесконечно большой, если для любого числа найдется номер , такой, что для всех выполняется неравенство .

Геометрически это означает, что какое бы мы число ни взяли, все  члены последовательности, кроме конечного числа их, лежат вне отрезка .

Тот факт, что бесконечно большая записывают, следующим образом . Последовательность расходится, если она не имеет предела или ее  предел равен бесконечности.

Определение:  Последовательность называется бесконечно малой, если .

Из определения предела последовательности непосредственно получаем, что последовательность будет бесконечно малой, если для любого положительного числа найдется число , такое, что для выполняется неравенство . Общие члены бесконечно малых последовательностей будем обозначать буквами греческого алфавита, например , , , …

Если последовательность бесконечно малая и все ее члены отличны от нуля, то последовательность – бесконечно большая, и обратно, если последовательность , , бесконечно большая, то  последовательность – бесконечно малая.

Суммой, разностью, произведением и частным двух последовательностей , называются соответственно последовательности , , , . При делении следует сделать оговорку, что все члены последовательности делителя отличны  от  нуля.

Для последовательностей справедливы следующие теоремы:

1. Алгебраическая сумма двух сходящихся последовательностей есть сходящаяся последовательность, ее предел равен соответствующей сумме пределов данных последовательностей, т.е. .

2. Произведение двух сходящихся последовательностей есть сходящаяся последовательность, ее предел равен произведению пределов данных последовательностей .

3. Если последовательности и сходятся, то последовательность сходятся и ее предел равен отношению пределов последовательностей и , т.е. , причем и   .

При вычислении пределов могут встретиться «неопределенности» вида   ; ; и другие.

Пример 1.  Вычислить предел: .

Пример 2.  Вычислить предел:

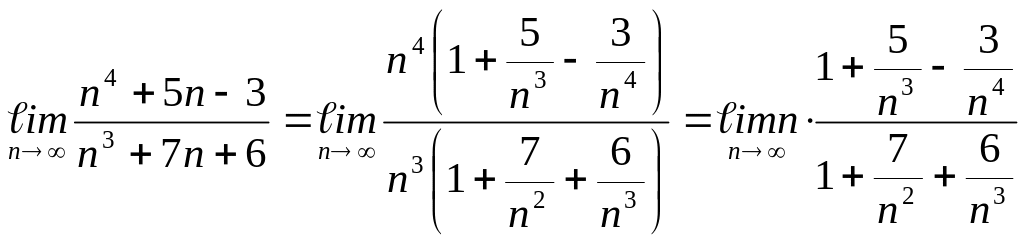
Так как, , то данная последовательность – бесконечно большая, т.е. .