Построение графиков функций

При построении графиков функций можно использовать следующую схему исследования:

1. найти область определения функции;

2. исследовать на четность и нечетность функцию;

3. найти точки разрыва функции;

4. найти асимптоты;

5. найти точки пересечения графика функции с координатными осями;

6. исследовать функцию на монотонность и экстремум;

7. определить интервалы выпуклости и вогнутости графика функции, точки прогиба;

8. при необходимости вычислить значения функции в дополнительных точках;

9. построить схематично график функции.

Пример 5.

Провести полное исследование функции и построить её график

1. Областью определения является множество .

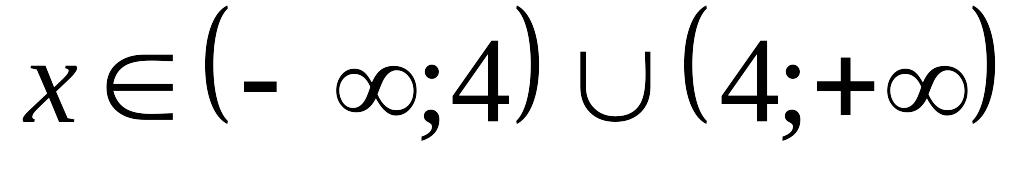2. Т.к. 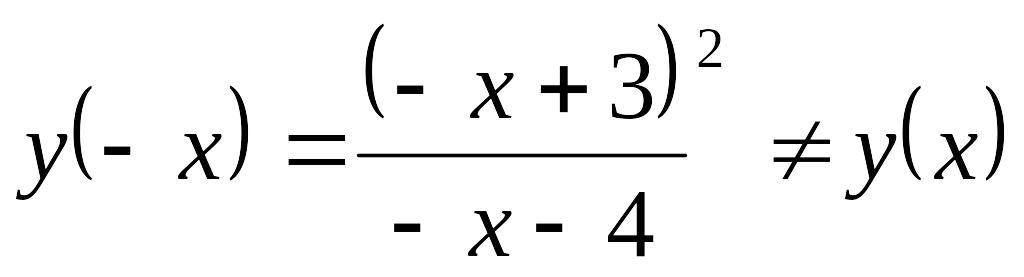, то функция не является ни четной, ни  нечетной.

3. Функция претерпевает разрыв в точке .

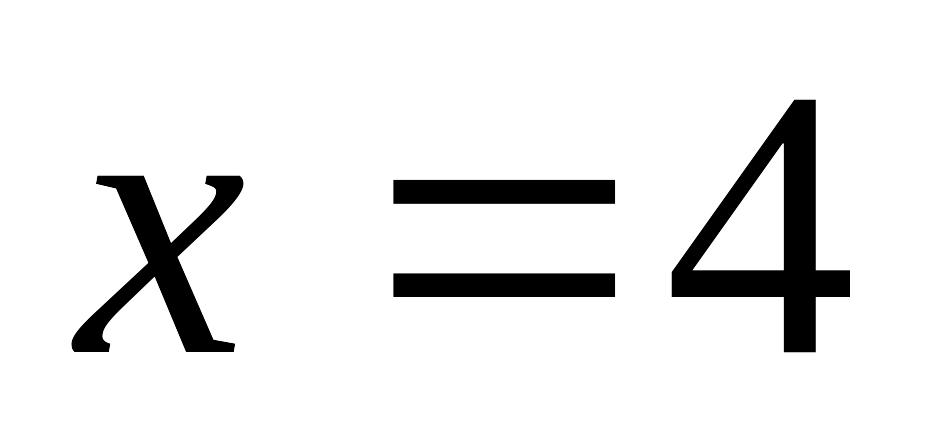4. Найдем асимптоты графиков функций:

а) Прямая является вертикальной асимптотой, т.к.

,

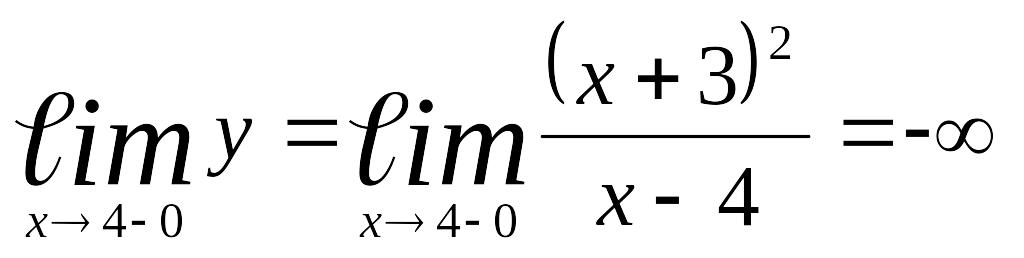б) Находим наклонные и горизонтальные асимптоты,

;

,

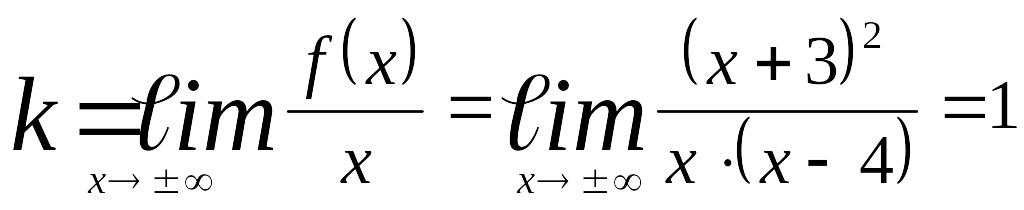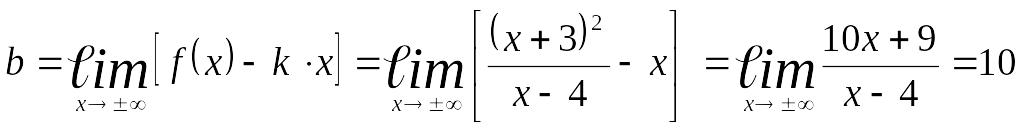является наклонной асимптотой.

5. Найдем точки пересечения графика функции с осями координат.

а) С осью : , т.е. точка пересечения с осью

– ,

б) С осью : , , , т.е. точка пересечения с  осью – .

6. Исследуем функцию на возрастание, убывание и экстремум. Для этого найдем производную функции.

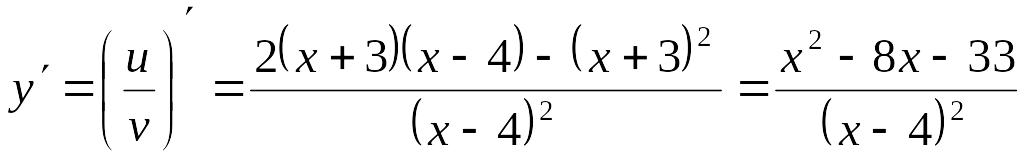
Из получаем 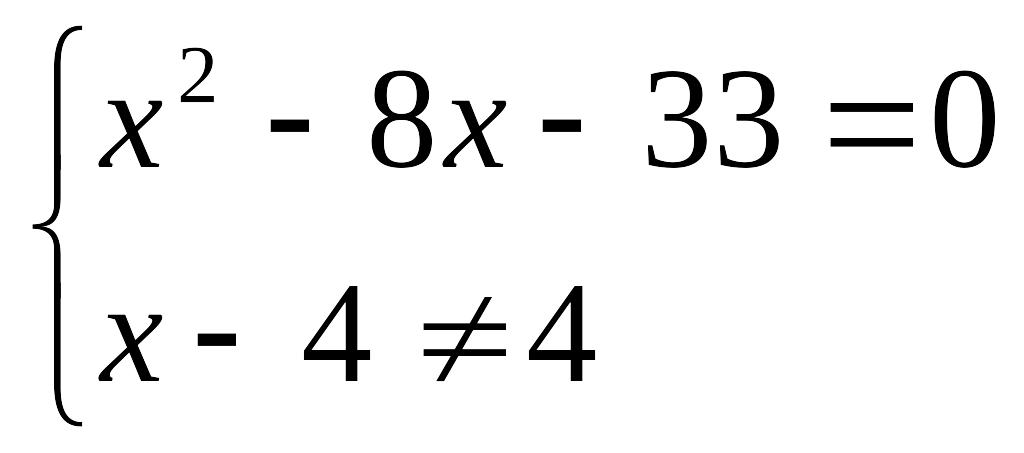, откуда , ,

+

–

+

–

-3

4

11

Так как на и производная положительна, т.е. , то график функции на указанных интервалах возрастает.

Так как на и производная отрицательна, т.е. , то на этих интервалах график функции убывает.

Так как при переходе через точки , производная функции меняет знак и эти точки входят в область определения функции, то , – точки экстремума. Причем – точка максимума: ; – точка минимума:

y_max= y(-3)=0

y_min= y(11)=28

7. Исследуем график функции на выпуклость, вогнутость и  определим точки перегиба. Для этого найдем вторую производную функции.

.

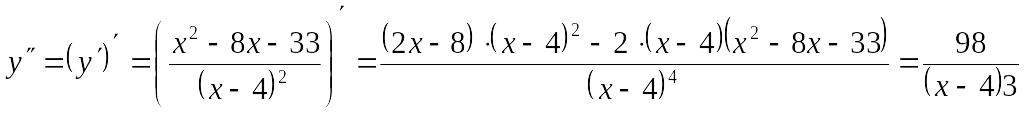Очевидно, что в интервале вторая производная меньше нуля, т.е. , и в этом интервале график функции является выпуклым вверх. В  интервале , и в этом интервале график функции является выпуклым вниз (вогнутым).

Несмотря на то, что при переходе через точку вторая производная меняет знак, она не является точкой перегиба, т.к. не входит в  область определения функции. Таким образом, точек перегиба у  графика функции нет.

8. Изобразим график функции схематично:

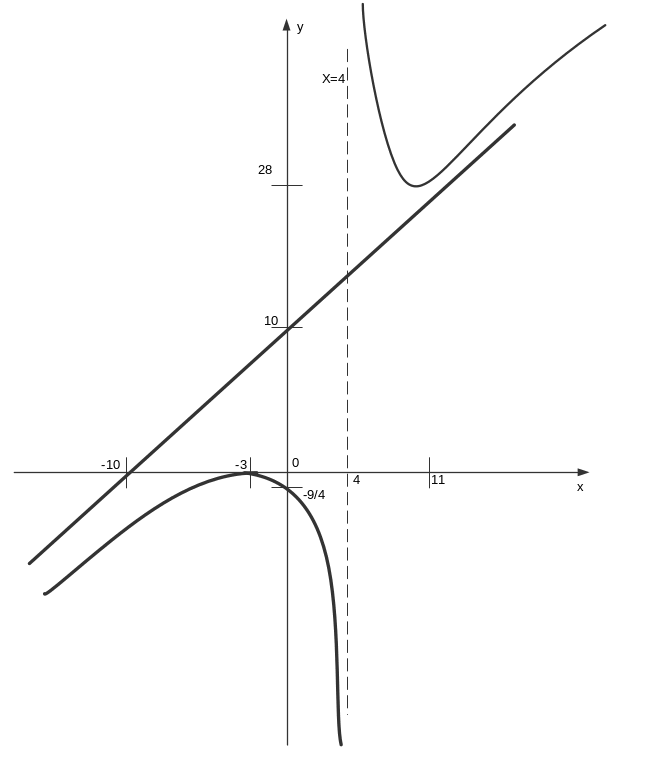
Вопросы для самоконтроля по теме «Дифференциальное исчисление функции одной переменной»

1. Определение производной функции, ее физический и  геометрический смысл.

2. Уравнение касательной и нормали к графику функции в точке.

3. Определение функции, дифференцируемой в точке.

4. Необходимое и достаточное условие дифференцируемости функции в  точке.

5. Дифференциал функции.

6. Правила дифференцирования, дифференциал суммы двух функций.

7. Дифференциал частного двух функций.

8. Дифференциал произведения двух функций.

9. Правило дифференцирования степенной функции.

10. Дифференцирование показательной, логарифмической функций.

11. Дифференцирование тригонометрических функций.

12. Дифференцирование обратных тригонометрических функций.

13. Правила нахождения производной функции, заданной неявно или параметрически.

14. Алгоритм исследования функции на возрастание, убывание и  экстремумы по первой производной.

15. Алгоритм исследования функции на экстремум по второй производной.

16. Производные высших порядков. Физический смысл второй производной. Примеры.

17. Общая схема исследования функций.

18. Правило Лопиталя раскрытия неопределенностей, возникающих при вычислении пределов функций.