Общие приемы интегрирования
Интегрирование элементарных функций
Элементарными дробями называются дроби следующих четырех типов:
I)
II)
III)
IV)
,
где
и
–
натуральные числа,
,
,
.
Интегралы I)
и II)
подстановкой
сводятся к табличным интегралам:
I.
,
II.
.
Интегралы III)
и IV)
также сводятся к табличным, путем
более сложных (в техническом плане)
упражнений и подстановок.
Пример 8.
Пример 9.
Интегрирование рациональных функций
Определение: Рациональная дробь называется правильной, если степень многочлена в числителе меньше степени многочлена в знаменателе. В противном случае рациональная дробь называется неправильной.
Выделяя из неправильной дроби ее целую часть (путем деления числителя на знаменатель), всегда можно представить ее в виде суммы многочлена и правильной рациональной дроби.
Разложение
конкретной правильной рациональной
дроби
на сумму элементарных дробей обычно
производят методом неопределенных
коэффициентов. Для этого разлагают
знаменатель
на произведение линейных и квадратичных
множителей, представляют данную дробь
в виде суммы дробей с неопределенными
коэффициентами в числителях. Затем
приводят элементарные дроби к общему
знаменателю
и приравнивают многочлен,
получившийся в числителе, многочлену
.
Для того чтобы два многочлена были тождественно равны, необходимо и достаточно, чтобы коэффициенты при одинаковых степенях у них были равны. Получаем тем самым систему алгебраических уравнений для нахождения неопределенных коэффициентов.
Пример 10.
Найти интеграл
Запишем подинтегральную функцию в виде суммы простейших дробей и приведем к общему знаменателю, имеем
Раскрываем скобки и приравниваем коэффициенты при одинаковых степенях
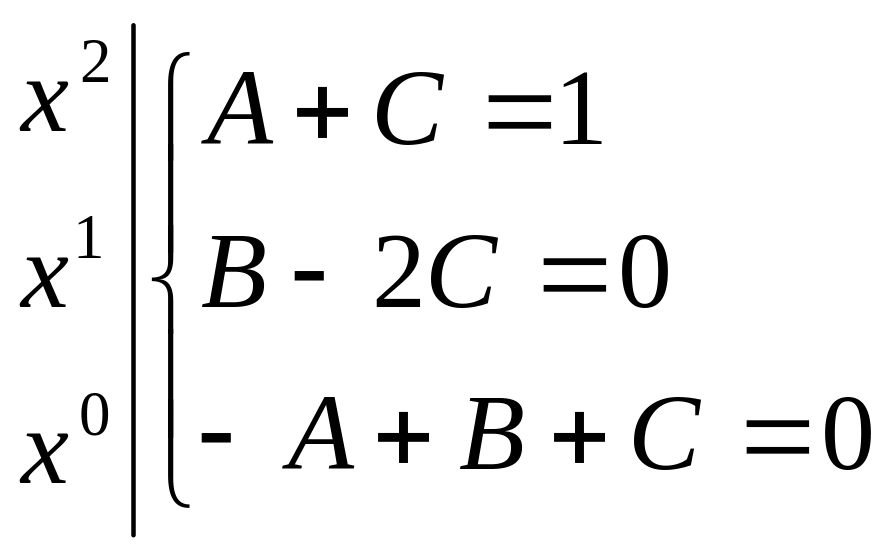
Решая эту систему, находим:
,
,
отсюда:
Интегрирование тригонометрических выражений
Определение: Рациональной функцией относительно и называется отношение двух многочленов относительно и .
В дальнейшем
символом
будем обозначать рациональную функцию
относительно переменных
и
.
Будем говорить, что функция
– нечетная относительно
,
если при замене
на
функция
меняет знак, т.е.
.
Если
,
то будем говорить, что такая функция
нечетна относительно
.
Функция
четна относительно
и
,
если при одновременной замене
на
,
на
функция не изменяется, т.е.
.
Заметим, что любая тригонометрическая функция аргумента рационально выражается через тангенс половинного угла. Действительно,
,
,
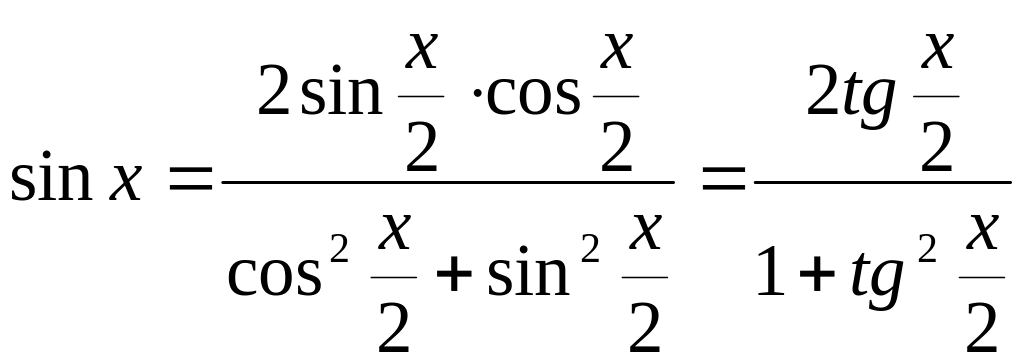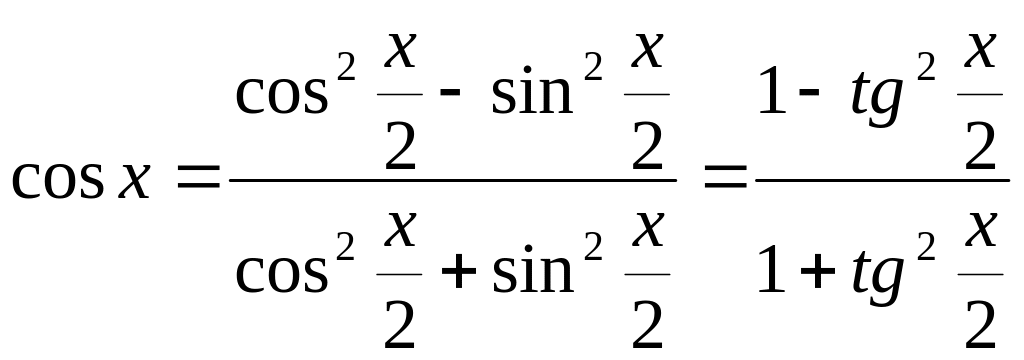а так как
,
,
,
рационально выражаются через
и
,
то они рационально будут выражаться
и через
.
Теорема 1. Интеграл
вида
подстановкой
приводится к интегралу от рациональной
функции
,
который, как было указано выше, всегда
выражается в элементарных функциях.
Пусть
,
тогда
,
,
,
Данная подстановка называется универсальной подстановкой.
Применим универсальную подстановку
Пример 11.
.
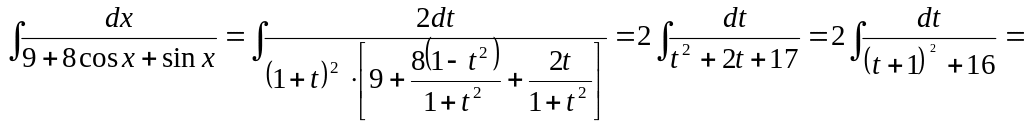
Теорема 2. Если
функция
нечетна относительно
,
то интеграл
подстановкой
приводится к интегралу от рациональной
функции.
Теорема 3. Если
имеет нечетный характер относительно
,
то подстановкой
интеграл
приводится к интегралу от
рациональной функции.
Пример 12.
.
Подинтегральная
функция нечетна относительно
.
Применим подстановку
,
тогда
.
Пример 13.
.
Теорема 4. Если
имеет четный характер относительно
и
,
то интеграл
подстановкой
приводится к интегралу от
рациональной функции.
Пример 14.
.
На практике при интегрировании тригонометрических функций часто еще используют известные формулы тригонометрии:
,
,
,
,
,
и другие.
Пример 15.
.
Пример 16.
.
Пример 17.
.
Интегрирование иррациональных функций
Простейшие интегралы от функций, содержащие иррациональности, являются табличными, либо сводятся к табличным с использованием свойств интеграла и замены переменной. В более сложных случаях основной подход состоит в сведении искомого интеграла к интегралу от рациональной функции с помощью подходящей замены переменной.
Теорема 1. Интеграл
вида
,
где
– натуральное число подстановкой
приводится к интегралу от рациональной
функции
или, как говорят, «рационализируется».
Следствие. Интеграл
вида
подстановкой
рационализируется.
Найти интегралы:
Пример 18.
,
где
.
Пример 19.
.
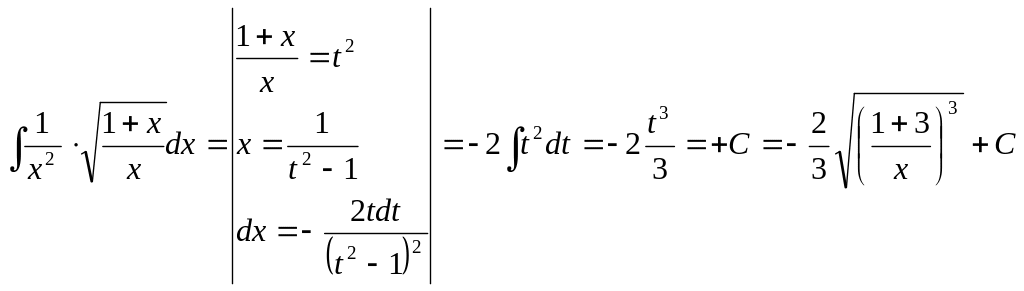Интегралы вида
,
,
,
где
– рациональная функция, находятся с
помощью подстановок
,
,
.