Вопросы для самопроверки по теме «Дифференциальное исчисление функции нескольких переменных»
1. Функция нескольких переменных.
2. Алгоритм нахождения экстремумов функции нескольких переменных.
3. Частные производные функции нескольких переменных.
4. Частные производные функции второго порядка, правила их нахождения.
5. Градиент функции в точке. Производной функции по направлению.
Тема 6. Неопределенный интеграл Первообразная функция и неопределенный интеграл
Определение: Будем
называть функцию
первообразной для функции
на данном промежутке, если в каждой
точке этого промежутка
.
Отыскание
первообразной по данной функции
составляет одну из основных задач
интегрального исчисления. Задача
отыскания по данной функции
ее первообразной решается неоднозначно:
если функция
– первообразная для
,
то функция
– любое число, также будет первообразной.
Определение: Множество
всех первообразных для функции
на промежутке
называется неопределенным интегралом.
Обозначается символом
(читается «интеграл эф от икс де икс»).
Функция
называется подинтегральной функцией,
– подинтегральным выражением,
– переменной интегрирования, символ
– знак интеграла.
Таким образом, по
определению
,
где
– какая-либо первообразная для
,
а
– произвольная постоянная. Отыскание
первообразной и отыскание неопределенного
интеграла от данной функции
называют интегрированием этой функции.
Интегрирование представляет
собой операцию, обратную дифференцированию.
Простейшие свойства неопределенного интеграла
Таблица основных интегралов
Свойство 1. Постоянный
множитель
можно выносить за знак интеграла:
.
Свойство 2. Неопределенный
интеграл от алгебраической суммы функций
равен алгебраической сумме интегралов
от этих функций:
.
Свойство 3. 
,
где
,
– числа,
.
Приведем таблицу основных интегралов. Часть формул этой таблицы непосредственно следует из определения интегрирования как операции, обратной дифференцированию, и таблицы производных.
1.
,
где
– действительное число,
,
2.
,
3.
,
4.
,
5.
,
6.
,
7.
,
8.
,
9.
,
,
10.
,
,
11.
,
,
12.
,
,
13.
,
,
14.
,
15.
.
Основные приемы интегрирования
Используя свойства неопределенных интегралов и таблицу основных интегралов, можно интегрировать некоторые элементарные функции (так называемое непосредственное интегрирование).
Рассмотрим несколько примеров.
,
,
,
,
,
.
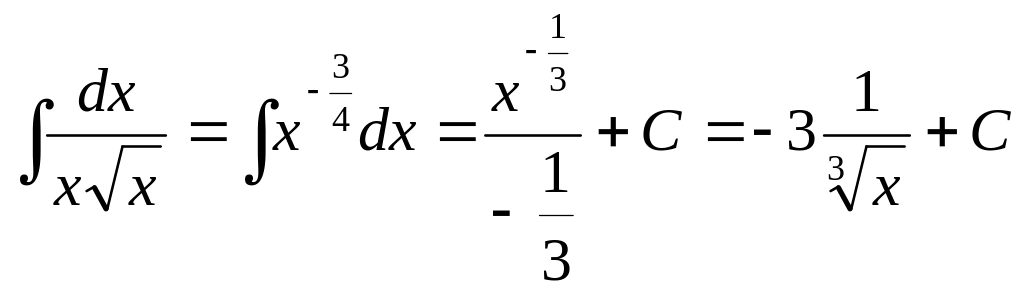Во многих случаях введение новой переменной интегрирования позволяет свести нахождение данного интеграла к нахождению табличного интеграла. Такой метод называется методом подстановки, а также методом переменной.
Рассмотрим функцию
,
где
– строго монотонная и непрерывно
дифференцируемая функция на некотором
промежутке. Если на соответствующем
промежутке изменения
функция интегрируема, то
(1)
После нахождения
интеграла
надо вместо
подставить его выражение через
.
Рассмотрим несколько примеров.
Пример 1.
Замена переменной в неопределенном интеграле чаще производится по формуле (1), прочитанной справа налево:
,
где
Пример 2.
Пример 3.
Интегрирование по частям
Пусть
и
непрерывно дифференцируемы на некотором
промежутке. Тогда
.
Эта формула называется формулой
интегрирования по частям. Правильнее
было бы назвать ее формулой частичного
интегрирования. При известных
и
она сводит нахождение интеграла от
после частичного интегрирования к
нахождению интеграла от
.
Сущностью
метода интегрирования по частям главным
является разумное разбиение подинтегрального
выражения на множители
и
.
Общих установок по этому вопросу нет.
Однако для некоторых типов интегралов,
сделать это возможно.
I тип. В
интегралах вида
,
,
,
где
– многочлен относительно
,
– число за
берут
,
все остальные множители обозначают
.
II тип. В
интегралах вида
,
,
,
,
полагают
,
все остальные за
.
III тип. В
интегралах вида
,
,
где
и
– числа можно принять за
любую функцию или
или
.
Пример 4.
Пример 5.
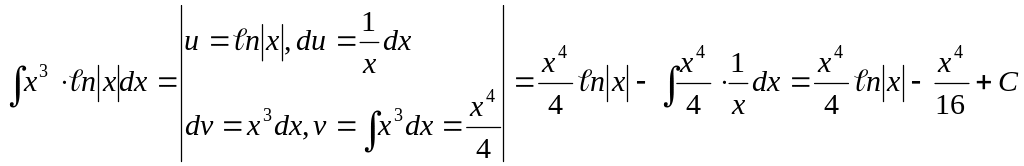
Иногда для получения окончательного результата приходится несколько раз последовательно применять формулу интегрирования по частям.
Пример 6.
Вычислим
отдельно, используя формулу интегрирования
по частям
Окончательно получаем:
,
где
Нахождение некоторых интегралов методом интегрирования по частям сводится к решению алгебраического уравнения, в котором неизвестным является искомый интеграл. Это относится к вычислению интегралов III типа.
Пример 7.
Вычислим
отдельно
Подставим полученное
выражение в искомое:
Раскрыв скобки, приведя подобные слагаемые, получим
,
отсюда
.