Вопросы для самоконтроля по теме «Введение в анализ»

1. Числовые множества.

2. Абсолютная величина числа и ее свойства.

3. Определение числовой последовательности, способы ее задания.

4. Свойства числовых последовательностей.

5. Бесконечно малые и бесконечно большие последовательности. Связь между ними.

6. Определение числовой функции, способы ее задания.

7. Свойства функций, классификация функций.

8. Понятие предела функции.

9. Предел функции в точке, на бесконечности.

10. Односторонние пределы.

11. Бесконечно большие и бесконечно малые функции, связь между ними.

12. Теоремы о пределе суммы, разности, произведения, частного функций, степени функции.

13. Методы раскрытия основных неопределенностей при вычислении пределов функции.

14. Первый и второй замечательные пределы.

15. Правила сравнения бесконечно малых функций. Перечислить основные эквивалентности для бесконечно малых функций.

16. Понятие о непрерывности функции.

17. Определение точек разрыва функции и их классификация.

18. Свойства непрерывных функций.

Тема 4. Дифференциальное исчисление функции одной переменной Производная функции. Геометрический и механический смысл производной

Рассмотрим функцию . Пусть функция определена в  некоторой окрестности точки . Дадим аргументу приращение , тогда функция получит приращение .

Определение:  Производной функции в точке называется предел отношения приращения функции к приращению аргумента при  стремлении приращения аргумента к нулю, если этот предел существует и конечен.

Производная функции в точке обозначается символами , , . Итак, по определению, .

Рассматривая задачу о проведении касательной к кривой, получили, что , т.е. . Отсюда следует геометрический смысл производной функции . Производная функции в точке равна  угловому коэффициенту касательной в точке к кривой, заданной уравнением .

Уравнение невертикальной касательной к кривой в ее точке можно записать в виде .

Определение:  Нормалью к кривой в ее точке называется прямая, проходящая через точку перпендикулярно касательной к  кривой в  этой  точке.

В силу условия перпендикулярности двух прямых можно записать уравнение нормали к кривой в точке в виде

, если .

Средняя скорость движения на различных промежутках различна. Чем меньше промежуток времени , тем точнее средняя скорость движения «характеризует» это движение в момент времени . Поэтому предел средней скорости движения при стремлении к нулю называют скоростью движения точки в данный момент времени и обозначают

.

Основные правила дифференцирования

Нахождение производной функции называется дифференцированием.

Основные правила:

Производная алгебраической суммы функций равна алгебраической сумме производных этих функций, т.е. , где , – дифференцированные функции.

Постоянный множитель можно выносить за знак производной.

Производные от произведения и частного равны соответственно

и 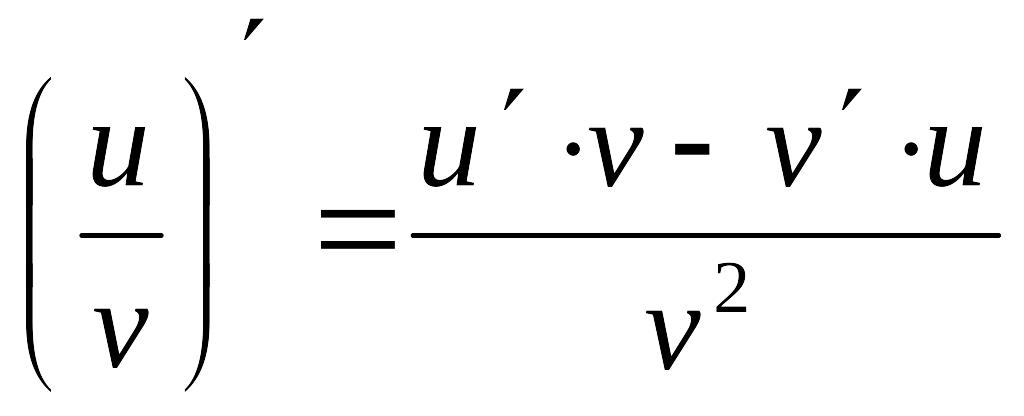при условии, что функция

отлична от нуля в рассматриваемой точке.

Определение:  Пусть , , причем область изменения второй функции входит в область определения первой. Тогда является сложной функцией независимой переменной , – промежуточная переменная.

Производная сложной функции по независимой переменной равна произведению этой функции по промежуточной переменной на производную промежуточной переменной по независимой переменной

При нахождении производных функций полезно знать формулы дифференцирования основных элементарных функций

1.

2.

3.

4.

5.

6.

7.

8.

9.

10.

11.

12.

13.

14.

15.

16.

Если зависимость между и задана в неявной форме уравнением , то для нахождения производной функции необходимо продифференцировать по обе части данного уравнения, рассматривая как функцию от . Из полученного уравнения первой степени (относительно ) находится .

Если функция аргумента задана параметрически уравнениями и  , то .

Пример 1.

Найти производные функций:

а) 

б) 

Пример 2.

Найти производную от функции, заданной неявно:

Продифференцируем обе части данного уравнения по . Получим Решим последнее уравнение относительно , получим .

Пример 3.

Найти производную функции, заданную параметрически:

Т.к. , то получим .

Пусть дифференцируема в точке .

Определение:  Дифференциалом функции в точке называется главная, линейная относительно , часть приращения функции.

Дифференциал функции обозначается через или . Из определения следует, что .

Дифференциал функции в точке равен произведению производной функции в этой точке на дифференциал независимой переменной.

Из определения дифференциала следует также, что нахождение производных или дифференциалов по существу представляет собой одну и  ту же задачу.