Тема 11. Комплексные числа Основные понятия
Решение многих задач сводится к решению алгебраических уравнений. Стремление сделать уравнения разрешимыми – одна из главных задач и причин расширения понятия числа. Так, например решение уравнения вида x2 = a на множестве рациональных чисел не имеет решения. Необходимость решения таких уравнений явилось одной из причин введения иррационального числа. Однако и действительных чисел недостаточно для того, чтобы решить любое алгебраическое уравнение. Например, уравнение х2 + 1 = 0 не имеет действительных корней, поэтому приходится расширять множество действительных чисел до нового множества
Корень уравнения х2 + 1 = 0 называется мнимой единицей и обозначается i2 = - 1.
Определение: Комплексным
числом
называется
выражение вида
,
где
и
– действительные числа, а символ
удовлетворяет
условию
.
Определение: Два комплексных числа называются равными, если соответственно равны их действительные части и коэффициенты при мнимой единице.
Определение: Сумма
комплексных чисел
и
определяется как комплексное число
.
Вычитание комплексных чисел определяется
как операция, обратная сложению:
Умножение двух комплексных чисел определяется следующим образом:
Частным от деления
комплексного
числа на число
называется
комплексное число такое
,
что
,
то есть
.
Таким образом,
частное от деления двух комплексных
чисел вычисляется по формуле:
.
Тригонометрическая
форма комплексного числа:
,
где
,
;
.
Показательная
форма комплексного числа:
.
Пример 1.
Найти сумму,
разность, произведение и частное
комплексных чисел
и 
,
результат записать в алгебраической,
тригонометрической и показательной
форме:
Найдем сумму
комплексных чисел:
.
Найдем разность
комплексных чисел:
.
Найдем произведение
комплексных чисел. Комплексные числа
перемножаются как двучлены, причем
заменяется на - 1.
Найдем частное комплексных чисел. Для этого числитель и знаменатель дроби надо умножить на число, сопряженное знаменателю.
Представим число
в тригонометрической и показательной
форме. Модуль данного числа равен
.
Данное комплексное число находится в
четвертой четверти комплексной плоскости,
так как
,
поэтому
.
Следовательно
.
Запишем число
в тригонометрической форме:
.
Записываем число
в показательной форме:
.
Аналогично записываются числа
и
в тригонометрической и показательной
формах.
Пример 2.
а) Вычислить:
б) Вычислить:
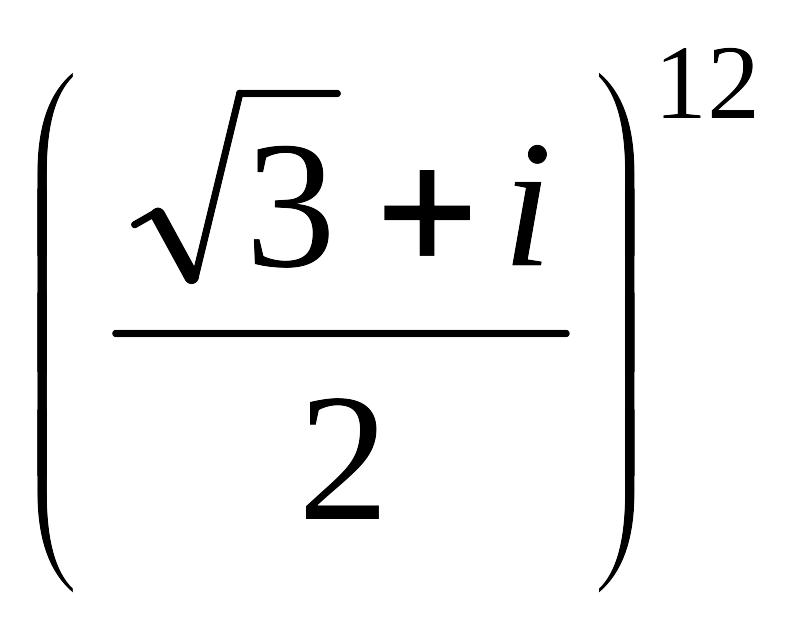
Перепишем данное
комплексное число в виде:
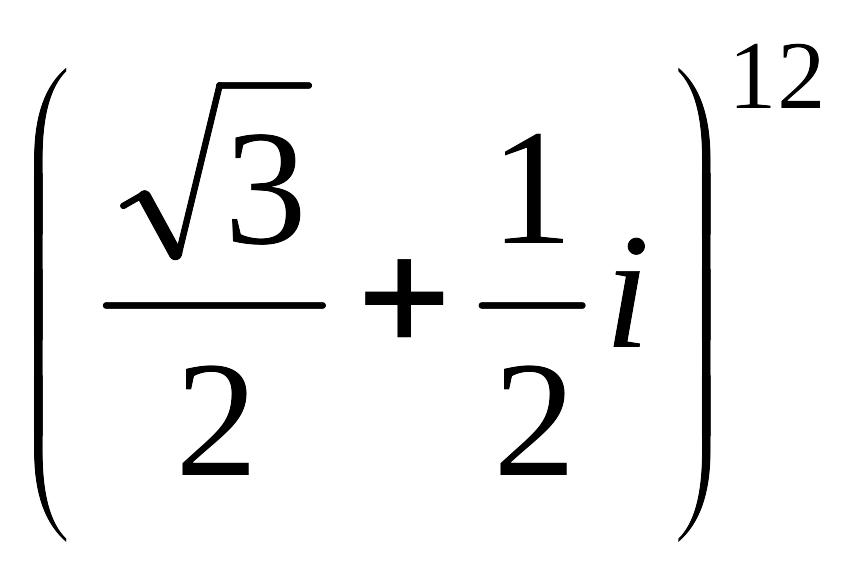и
представим его в тригонометрической
форме. Модуль данного числа равен
,
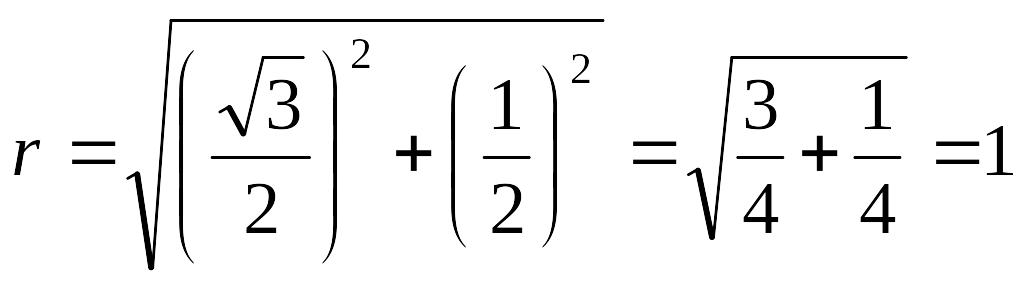при вычислении аргумента учитываем,
что
и
.
Значит
,
отсюда
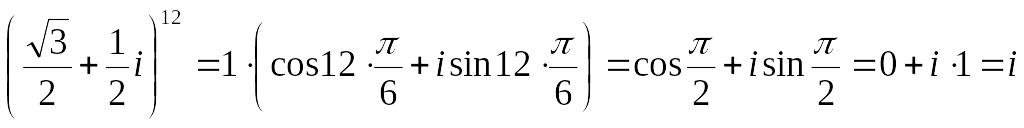
Вопросы для самоконтроля по теме «Комплексные числа»
1. Комплексные числа и их геометрическая интерпретация.
2. Действия над комплексными числами, заданными в алгебраической форме.
3. Действия над комплексными числами, заданными в тригонометрической форме.
4. Действия над комплексными числами, заданными в показательной форме. Формулы Эйлера.