
- •Математика
- •Введение
- •Студенты должны знать:
- •Приобрести практические навыки:
- •Содержание разделов дисциплины «Математика»
- •Раздел 1. Основы алгебры и анализа
- •Раздел 2. Интегральное исчисление. Обыкновенные дифференциальные уравнения. Ряды
- •Раздел 3. Теория вероятностей
- •Раздел 4. Численные методы и оптимизационные задачи
- •Контрольная работа № 1 включает задания по следующим темам:
- •Тема 1. Элементы линейной алгебры
- •Определители третьего порядка
- •Применение определителей к решению систем линейных уравнений
- •Решение систем линейных уравнений с – неизвестными
- •Рассмотрим решения типовых заданий по теме «Линейная алгебра»
- •Вопросы для самоконтроля по теме «Линейная алгебра»
- •Тема 2. Элементы аналитической геометрии Прямоугольная декартова система координат на плоскости
- •Кривые второго порядка
- •Вопросы для самоконтроля по теме «Аналитическая геометрия»
- •Тема 3. Введение в анализ Последовательность, предел последовательности
- •Предел функции
- •Основные теоремы о пределах функции
- •Некоторые приемы вычисления пределов функций
- •Имеем , тогда . Непрерывность функций
- •Вопросы для самоконтроля по теме «Введение в анализ»
- •Тема 4. Дифференциальное исчисление функции одной переменной Производная функции. Геометрический и механический смысл производной
- •Основные правила дифференцирования
- •Основные теоремы дифференциального исчисления
- •Возрастание и убывание функций
- •Экстремумы функции
- •Точки перегиба. Выпуклость и вогнутость
- •Асимптоты плоских кривых
- •Построение графиков функций
- •Вопросы для самоконтроля по теме «Дифференциальное исчисление функции одной переменной»
- •Тема 5. Дифференциальное исчисление функции нескольких переменных Функции нескольких переменных
- •Понятие предела для функции двух переменных
- •Определение: Градиентом функции называется вектор с координатами , в точке . По определению
- •Экстремумы функций нескольких переменных
- •Вопросы для самопроверки по теме «Дифференциальное исчисление функции нескольких переменных»
- •Тема 6. Неопределенный интеграл Первообразная функция и неопределенный интеграл
- •Простейшие свойства неопределенного интеграла
- •Основные приемы интегрирования
- •Общие приемы интегрирования
- •Интегрирование рациональных функций
- •Вопросы для самоконтроля по теме «Неопределенный интеграл»
- •Тема 7. Определенный интеграл
- •Формула Ньютона-Лейбница
- •Тема 8. Обыкновенные дифференциальные уравнения
- •Дифференциальное уравнение первого порядка
- •Уравнения с разделяющимися переменными
- •Однородные уравнения
- •Линейные уравнения
- •Уравнения -го порядка, допускающие понижение порядка
- •Линейные дифференциальные уравнения второго порядка с постоянными коэффициентами
- •Вопросы для самоконтроля по теме «Дифференциальные уравнения»
- •Тема 9. Ряды Общие сведения
- •Свойства рядов
- •Ряды с неотрицательными членами
- •Знакопеременные ряды
- •Степенные ряды. Интервал сходимости степенного ряда
- •Вопросы для самоконтроля по теме «Ряды»
- •Тема 10. Элементы Теории вероятностей Формулы комбинаторики
- •Совместные и несовместные события
- •Случайные величины
- •Числовые характеристики дискретной случайной величины
- •Непрерывные случайные величины
- •Математическое ожидание и дисперсия. Мода и медиана
- •Вопросы для самопроверки по теме «Теория вероятностей»
- •Тема 11. Комплексные числа Основные понятия
- •Вопросы для самоконтроля по теме «Комплексные числа»
- •Тема 12. Элементы линейного программирования Общая постановка задачи
- •Решение систем линейных неравенств с двумя переменными
- •Графический метод. Выбор оптимального варианта
- •Алгоритм симплексного метода
- •Транспортная задача
- •Метод потенциалов
- •Вопросы для самоконтроля по теме «Линейное программирование»
- •Контрольная работа № 1 (первый семестр)
- •Контрольная работа № 2 (второй семестр)
- •Контрольная работа № 3 (третий семестр)
- •Контрольная работа № 4 (четвертый семестр)
- •Методические указания по выполнению и оформлению контрольных работ
- •Формы и содержание отчетности студентов
- •Вопросы к экзамену (1 семестр)
- •Вопросы к зачету (2 семестр)
- •Вопросы к зачету (3 семестр)
- •Вопросы к экзамену (4 семестр)
- •Список литературы
- •Математика
- •1 62600, Череповец, ул. Сталеваров, 44
Некоторые приемы вычисления пределов функций
Для того, чтобы найти предел элементарной функции, когда аргумент стремится к значению, принадлежащему области определения этой функции, нужно в выражении функции вместо аргумента подставить его предельное значение.
![]() .
.
Под знаком предела можно производить тождественные преобразования аналитического выражения, задающего функцию, не принимая во внимание поведение функции в предельной точке. В частности, например, под знаком предела можно производить сокращение дроби на множитель, обращающийся в предельной точке в нуль (но не равный нулю в близи этой точки!).
Пример 9.
![]()
Пример 10.
![]()
Разложим числитель и знаменатель на множители, используя формулы
![]() ,
,
![]() ,
где
,
,
,
где
,
,
![]() – числа,
– числа,
![]() ,
,
– корни квадратного трехчлена.
Получаем:
,
,
– корни квадратного трехчлена.
Получаем:
![]() .
.
Пример 11. Найти
![]()
Числитель и знаменатель дроби умножим на выражение, сопряженное числителю, получаем:
![]() .
.
Пример 12. Найти
![]() В данном примере при выяснении вида
неопределенности видим, что таковой не
имеется.
В данном примере при выяснении вида
неопределенности видим, что таковой не
имеется.
Имеем , тогда . Непрерывность функций
Определение: Функция
,
определенная в точке
![]() и некоторой окрестности, называется
непрерывной в точке
,
если предел функции при
и некоторой окрестности, называется
непрерывной в точке
,
если предел функции при
![]() равен значению функции в точке
:
равен значению функции в точке
:
![]() .
.
Любая элементарная функция непрерывна в ее области определения.
Определение: Если функция определена в окрестности точки (кроме, быть может, самой точки ) и не является непрерывной в этой точке, то ее называют разрывной в точке . В этом случае точку называют точкой разрыва .
Определение: Функция
называется непрерывной на интервале
![]() ,
если она непрерывна в каждой точке
интервала. Функция
называется непрерывной на отрезке
,
если она непрерывна в каждой точке
интервала. Функция
называется непрерывной на отрезке
![]() ,
если она непрерывна на интервале
и, кроме того, непрерывна справа
в точке
и непрерывна слева в точке
.
,
если она непрерывна на интервале
и, кроме того, непрерывна справа
в точке
и непрерывна слева в точке
.
Для непрерывности функции на отрезке не требуется непрерывность этой функции на концах отрезка. В точках и требуется только односторонняя непрерывность функции для левого конца непрерывность справа, для правого непрерывность слева.
Из определения точки разрыва функции получаем, что точка является точкой разрыва функции , если выполняется одно из условий: или функция определена в точке , но не является непрерывной в этой точке, или функция не определена в точке .
В первом случае принадлежит области определения функции, во втором случае не принадлежит области определения функции. Для основных элементарных функций возможен только второй случай.
Пусть – точка разрыва функции . При этом называется точкой разрыва первого рода, если функция имеет конечные пределы справа и слева в этой точке. Во всех остальных случаях называется точкой разрыва второго рода. Если – точка разрыва I рода функции , то график этой функции в точке может иметь лишь конечный скачок. Если же – точка разрыва I рода функции , то, по крайней мере, один из пределов справа или слева в точке не существует или равен бесконечности.
Пример 13. Исследовать функцию на непрерывность и построить её график
![]()
![]()
Эта функция
определена на интервалах
![]() ,
,
![]() ,
,
![]() ,
где она задана непрерывными элементарными
функциями. Внутри каждого интервала
указанные элементарные функции не имеют
точек разрыва, следовательно, разрыв
возможен только в точках перехода от
одного аналитического
выражения к другому, т.е. в точках
,
где она задана непрерывными элементарными
функциями. Внутри каждого интервала
указанные элементарные функции не имеют
точек разрыва, следовательно, разрыв
возможен только в точках перехода от
одного аналитического
выражения к другому, т.е. в точках
![]() и
и
![]() .
.
Для точки имеем:
![]() ,
,
![]() ,
,
![]()
Так как
![]() ,
то функция
в точке
имеет разрыв первого рода. Для точки
находим
,
то функция
в точке
имеет разрыв первого рода. Для точки
находим
![]() ,
,
![]() .
.
Значение функции в самой точке равно .
![]() .
.
Так как
![]() ,
то функция
в точке
имеет разрыв первого рода. Изобразим
график функции
,
то функция
в точке
имеет разрыв первого рода. Изобразим
график функции

![]()







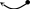


Пример 14. Исследовать
данную функцию на непрерывность
в указанных точках
![]() ;
;
![]() ,
,
![]() .
.
Для точки имеем:
![]() ,
,
![]() ,
,
т.е. в точке функция имеет разрыв второго рода (терпит бесконечный разрыв). Для точки имеем:
![]() ,
,
![]() ,
,
![]() .
.
Следовательно, в точке функция непрерывна.
