Случайные величины

Закон распределения вероятностей дискретной

случайной величины.

Определение:  Случайной величиной называется величина, которая в  результате опыта может принять любые заранее неизвестные значения. Различают дискретные и непрерывные случайные величины.

Определение:  Дискретной случайной величиной называется такая, значения которой есть конечное или счетное множество фиксированных величин. Для описания поведения дискретной случайной величины задают все значения , , , …, , которые она может принять, и  вероятности появления этих значений , , , …, .

Определение:  Законом распределения вероятностей (рядом распределения) дискретной случайной величины называется последовательность возможных значений случайной величины и  соответствующих им вероятностей, причем :

			. . .
			. . .

Ряд распределения можно задать графически, откладывая на горизонтальной оси значения , а на вертикальной – соответствующие им значения вероятностей. Графическое представление ряда распределения называется многоугольником распределения.

Для дискретной случайной величины можно ввести понятие функции распределения , которая равна вероятности случайного события, состоящего в том, что ДСВ примет одно из возможных значений, меньших некоторого значения , т.е. .

Если дискретные значения случайной величины расположены в  порядке возрастания , , , …, , то можно задать в виде

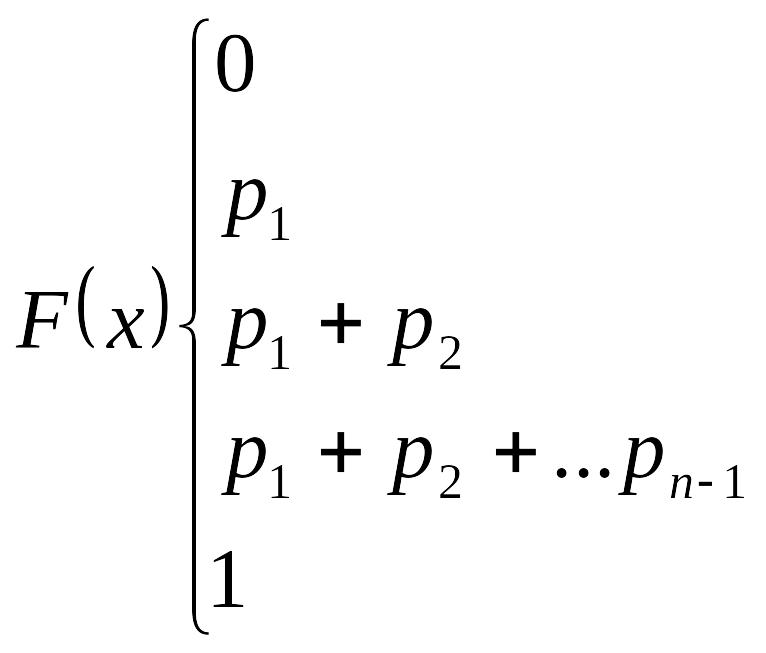
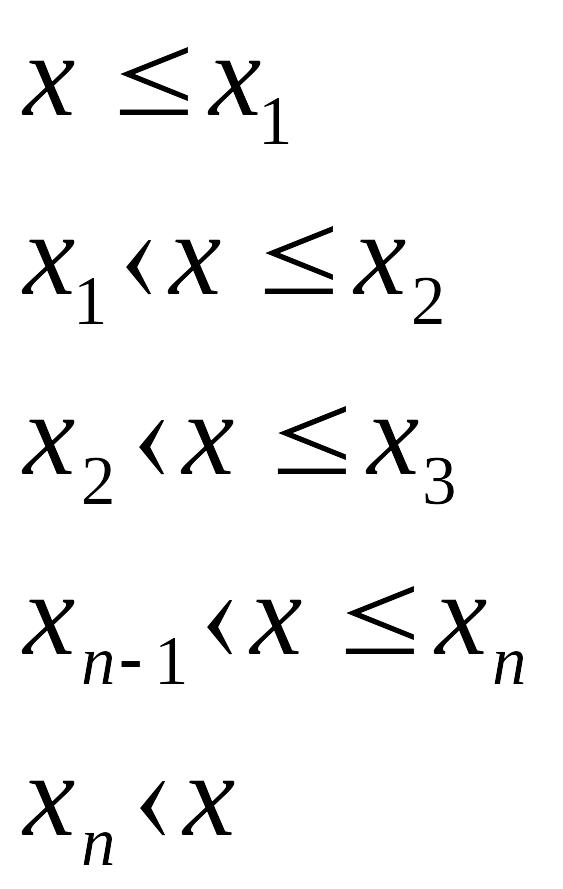
Функцию распределения можно представить графически в виде ступенчатой функции

Определение:  Биноминальным называют закон распределения ДСВ – числа появления события в независимых испытаниях, в каждом из  которых вероятность появления события равна ; вероятность возможного значения (числа появлений события) вычисляют по  формуле Бернулли:

Если число испытаний велико, а вероятность появления события в  каждом испытании очень мала, то используют приближенную формулу

,

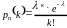где – число появлений события в независимых испытаниях, , и  говорят, что случайная величина распределена по закону Пуассона. Закон распределения Пуассона является предельным случаем биноминального распределения, его часто еще называют «законом редких чисел», т.к. , , . Обычно для его применения достаточно ; .

Задача 9.  Баскетболист делает три штрафных броска. Вероятность попадания при каждом броске равна 0,7. Построить ряд распределения числа попаданий мяча в корзину.

Решение:

Пусть – случайная величина числа попаданий мяча в корзину. Баскетболист может не попасть ни разу, один раз, два раза и все три раза,

т.е. , , , . Вероятности вычисляем по формуле Бернулли,

при этом ; ;

Проверим выполнение .

Ряд распределения случайной величины числа попаданий мяча в  корзину при трех бросках имеет вид

Составим функцию распределения :

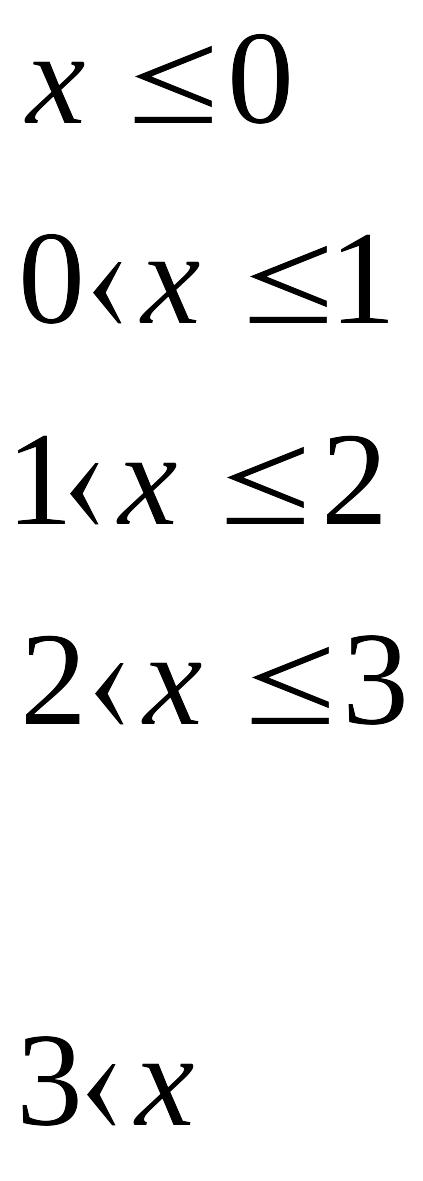
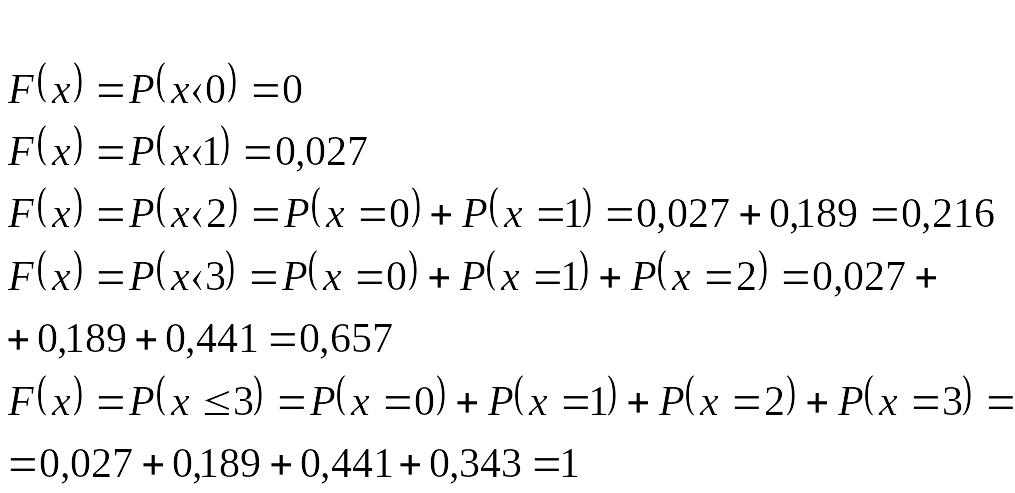
Построим функцию распределения

1

0,8

0,6

0,4

0,2

0

1

2

3

х

Задача 10.  В партии из 25 кожаных курток пять имеют скрытый дефект. Покупают три куртки. Найти закон распределения числа дефектных курток  среди купленных. Построить многоугольник распределения.

Решение:

Пусть – случайная величина числа дефектных курток среди купленных, она может принимать значения: , , , . Для определения вероятности появления каждого из этих значений воспользуемся формулой:

,

где ; ; ; – число дефектных курток, – курток без  дефекта; .

Вычисляем соответствующие вероятности:

;

;

;

;

Проверим условие , т.е.

.

Построим многоугольник распределения.

0,2

многоугольник распределения

0,5

0,4

0,3

0,1

4

0

1

2

3

				Закон распределения числа дефектных курток

Задача 11.  Учебник издан тиражом 100 000 экземпляров. Вероятность того, что учебник сброшюрован неправильно, равна 0,0001. Найти вероятность того, что тираж содержит ровно пять бракованных книг.

Решение:

По условию, , , . События, состоящие в том, что книги сброшюрованы неправильно, независимы, число велико, а  вероятность мала, поэтому воспользуемся распределением Пуассона . Найдём : .

Искомая вероятность .