Транспортная задача

Транспортная задача – одна из распространенных задач линейного программирования. Ее цель – разработка наиболее рациональных путей и  способов транспортирования товаров, устранение чрезмерно дальних, встречных, повторных перевозов.

В общем виде задачу можно представить следующем образом: в пунктах производства …, имеется однородный груз в количестве соответственно …, . Этот груз необходимо доставить в пунктов назначения …, в качестве соответственно …, . Стоимость перевозки единицы груза (тариф) из пункта в пункт равна .

Потребуется составить план перевозок, позволяющий вывести все грузы и имеющий минимальную стоимость.

Если , то задача называется закрытой (ЗТЗ).

Если , то задача называется открытой (ОТЗ).

Обозначим через количество груза, перевозимого из пункта в пункт .

Рассмотрим ЗТЗ. Ее условия запишем в распределительную таблицу, которую будем использовать для нахождения решения.

			…
			…
			…
...	…	…	…	…
			…

Математическая модель закрытой транспортной задачи имеет вид:

при ограничениях:

Оптимальным решением является матрица удовлетворяющая системе ограничений и доставляющая минимум целевой функции.

Для решения транспортной задачи разработан специальный метод, имеющий этапы:

• нахождение исходного опорного решения;

• проверка этого решения на оптимальность;

• переход от одного опорного решения к другому.

Нахождение исходного опорного решения

Условия задачи и ее исходное опорное решение будем записывать в  распределительную таблицу. Клетки, в которые поместим грузы, называются занятыми, им соответствуют базисные переменные опорного решения. Остальные клетки незанятые или пустые, им соответствуют свободные переменные. В верхнем правом углу каждой клетки будем записывать тарифы. Существует несколько способов нахождения исходного опорного решения: метод минимального тарифа; метод северо-западного угла и др.

Рассмотрим метод минимального тарифа. Согласно этому методу, грузы распределяются в первую очередь в те клетки с наименьшими тарифами с  учетом оставшихся запасов у поставщиков и удовлетворения спроса потребителей. Процесс распределения продолжают до тех пор, пока все грузы от поставщиков не будут вывезены, а потребители не будут удовлетворены. При распределении грузов может оказаться, что количество занятых клеток меньше, чем

В этом случае недостающие их число заполняется клетками с  нулевыми поставками, такие клетки называют условно занятыми.

Нулевые поставки помещают в незанятые клетки с учетом наименьшего тарифа таким образом, чтобы в каждой строке и столбце было не менее чем по одной занятой клетке.

Пример 3.  На складах , , имеются запасы продукции в  количествах 90; 400; 110 т соответственно. Потребители , , должны получить эту продукцию в количествах 140; 300; 160 т соответственно. Найти такой вариант прикрепления поставщиков к  потребителям, при  котором сумма затрат на перевозки была бы минимальной. Расходы по  перевозке 1 т продукции заданы матрицей (усл. ед.)

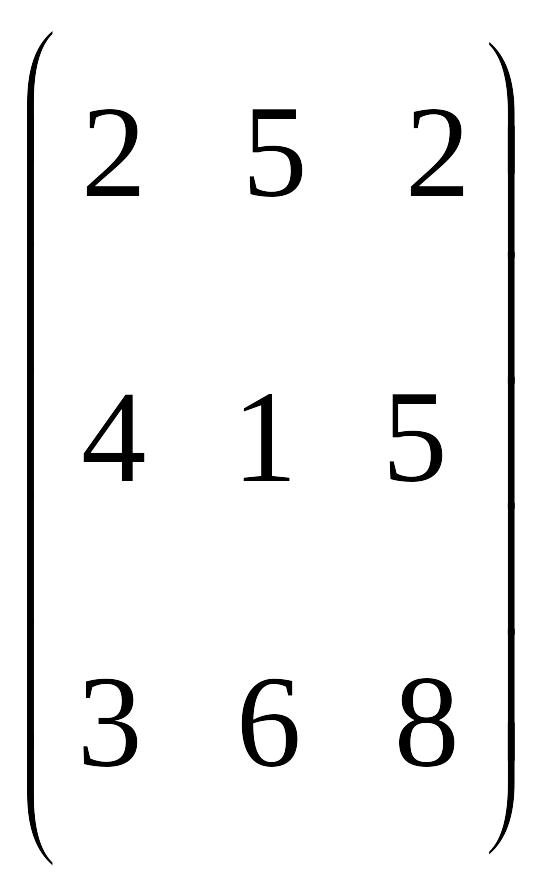
Проверим, является ли данная транспортная задача закрытой:

т,

т,

, следовательно, данная транспортная задача закрытая. Найдем исходное опорное решение по методу минимального тарифа.

			5

Число занятых клеток равно , т.е. условие невырожденности выполнено. Получим исходное опорное решение, которое запишем в виде матрицы:

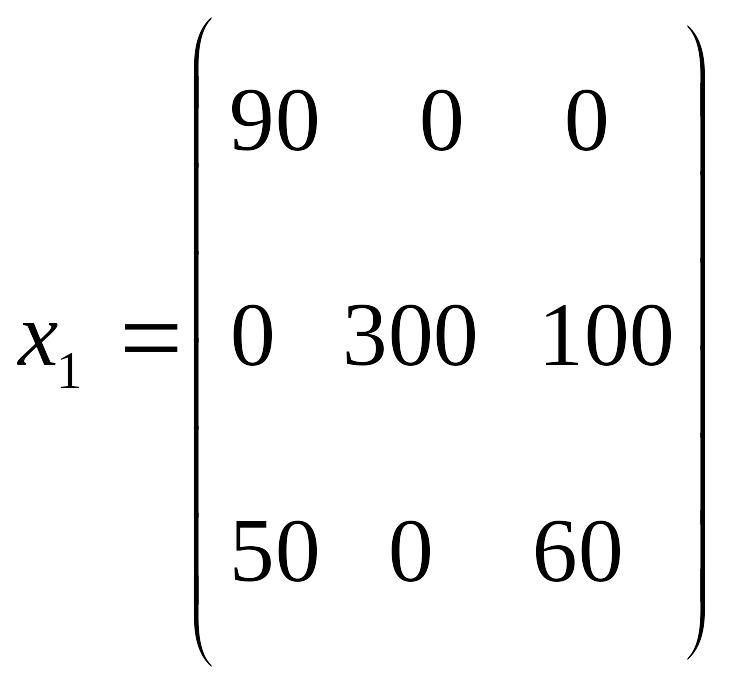
Стоимость перевозки при исходном опорном решении составляет:

усл. ед.