Графический метод. Выбор оптимального варианта

С геометрической точки зрения в задаче линейного программирования ищется такая угловая точка или набор точек из допустимого множества решений, на котором достигается самая верхняя (нижняя) линяя уровня, расположенная дальше (ближе) остальных в направлении наискорейшего роста.

Для нахождения экстремального значения целевой функции при  графическом решении задач линейного программирования используют  вектор на плоскости , который обозначим . Этот вектор показывает направление наискорейшего изменения целевой функции, он равен

,

где и – единичные векторы по осям и соответственно.

Координаты вектора являются коэффициенты целевой функции .

Алгоритм решения задач

1. Находим область допустимых решений системы ограничений задачи.

2. Строим вектор .

3. Проводим линию уровня 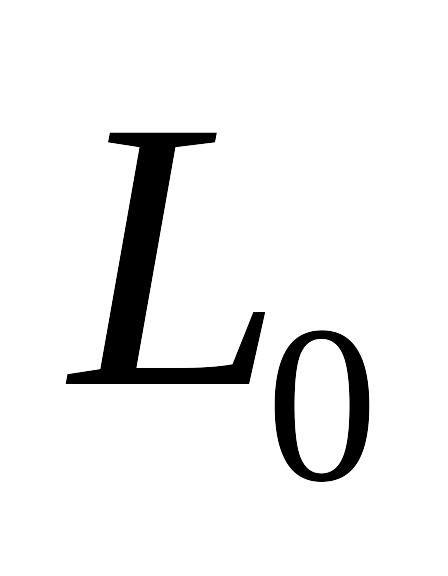, которая перпендикулярна .

4. Линию уровня перемещаем по направлению вектора для задачи на максимум и в направлении, противоположном , для задачи на минимум.

Перемещение линий уровня производится до тех пор, пока у него не  окажется только одна общая точка с областью допустимых решений. Эта точка, определяющая единственное решение задачи линейного программирования, и будет точкой экстремума.

Если окажется, что линия уровня параллельна одной из сторон ОДР, то  в  таком случае экстремум достигается во всех точках соответствующей  стороны, а задача линейного программирования будет иметь бесчисленное множество решений. Говорят, что такая задача линейного  программирования имеет альтернативный оптимум, и ее решение находится по формуле:

,

где ,

и – оптимальные решения в условиях ОДР.

Задача линейного программирования может быть неразрешима, когда определяющие ее ограничения окажутся противоречивыми.

5. Находим координаты точки экстремума и значение целевой функции в ней.

Пример 1.  Для изготовления двух видов продукции и используют четыре вида ресурсов , . Запасы ресурсов, число единиц ресурсов, затрачиваемых на изготовление единицы продукции, приведены в таблице:

Вид ресурса	Запас ресурса	Число единиц ресурсов, затрачиваемых на изготовление единицы
		продукции	продукции
	18	1	3
	16	2	1
	5	-	1
	21	3	-

Прибыль, получаемая от единицы продукции и , – соответственно 2  и 3 руб. Необходимо составить такой план производства продукции, при котором прибыль от ее реализации будет максимальной.

Решение:

Составим экономико-математическую модель задачи. Обозначим и    – число единиц продукции соответственно и , запланированных к  производству. Связь между потреблением ресурсов и их запасами выразится системой неравенств

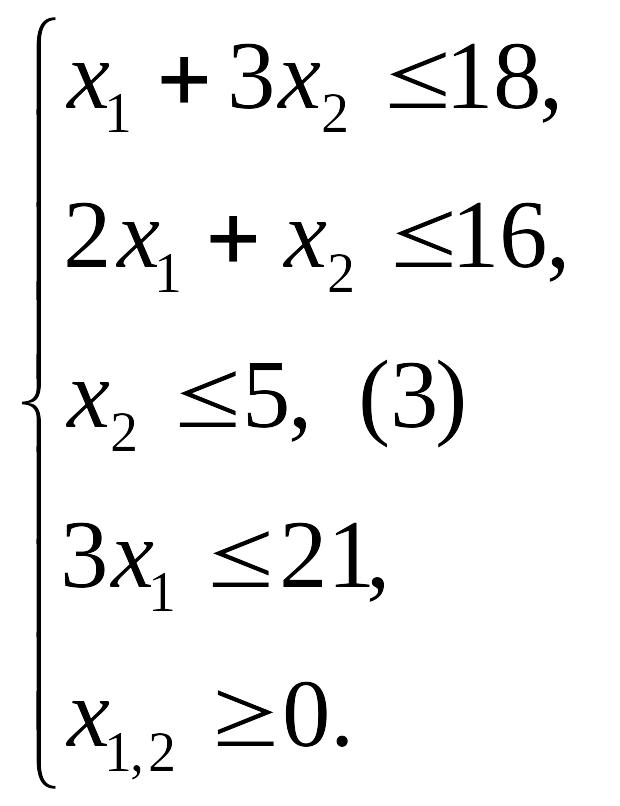
Суммарная прибыль составляет руб. от реализации продукции и   руб. – от реализации продукции , т.е. .

Итака, экономико-математическая модель задачи: при которой функция принимает максимальное значение.

Изобразим многогранник решений.

Построим вектор

Перемещая линию уровня в направлении вектора , найдем оптимальное решение в угловой точке , определяемое системой уравнений

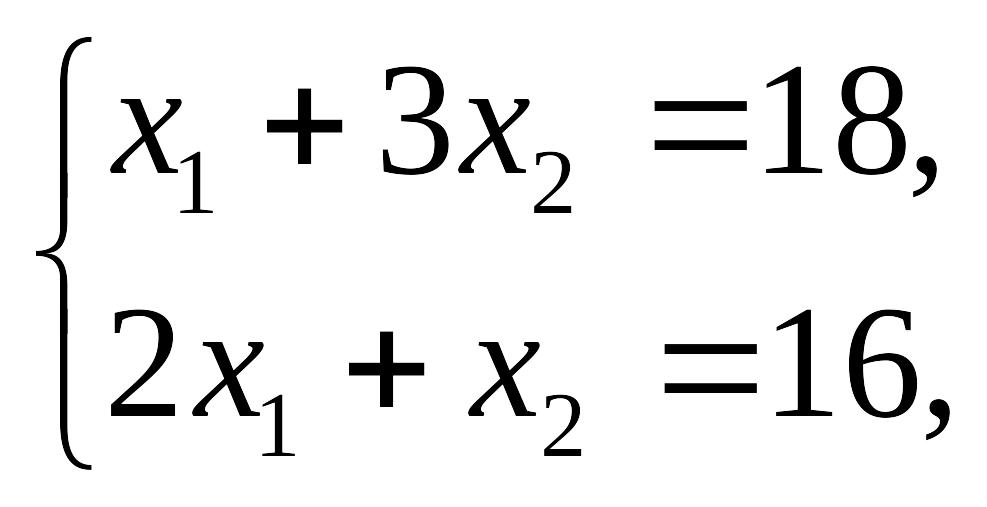
откуда т.е. .

М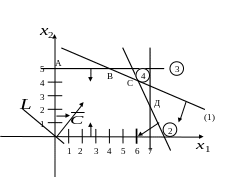 аксимум линейной функции равен т.е. максимальная прибыль в 24 руб. достигается при производстве 6 ед. продукции и 4 ед. продукции .