Числовые характеристики дискретной случайной величины

Характеристикой среднего значения случайной величины служит математическое ожидание.

Определение:  Математическим ожиданием дискретной случайной величины называют сумму произведений всех её возможных значений на  их вероятности: .

Если дискретная случайная величина принимает счетное множество возможных значений, то , причем математическое ожидание существует, если ряд в правой части равенства сходится абсолютно.

Математическое ожидание биноминального распределения равно произведению числа испытаний на вероятность появления события в  одном испытании: .

Характеристиками рассеяния возможных значений случайной величины вокруг математического ожидания, в частности, дисперсия и  среднее квадратическое отклонение.

Определение:  Дисперсией случайной величины Х называют математическое ожидание квадрата отклонения случайной величины от  её  математического ожидания: .

Дисперсию удобно вычислять по формуле .

Дисперсия биноминального распределения равна произведению числа  испытаний на вероятности появления или не появления события в  одном испытании: .

Определение:  Средним квадратическим отклонением случайной величины называют квадратный корень из дисперсии: .

Задача 12.  Два консервных завода поставляют продукцию в магазин в  пропорции 2:3. Доля продукции высшего качества на первом заводе составляет 90 %, а на втором – 80 %. В магазине куплено 3 банки консервов. Найти и , где – число банок с продукцией высшего качества.

Решение:

Вычислим вероятность появления события – куплена банка с  продукцией высшего качества. По формуле полной вероятности имеем:

.

Закон распределения дискретной случайной величины можно определить, используя формулу Бернулли:

, где , . Случайная величина может принимать значения ; ; ; . Закон её распределения примет вид

Тогда ,

,

.

Непрерывные случайные величины

Непрерывные случайные величины характеризуются тем, что их значения могут сколь угодно мало отличаться друг от друга.

Вероятность события (где – значение непрерывной случайной величины, а – произвольно задаваемое значение), рассматриваемая как  функция от , называется функцией распределения вероятностей:

.

Часто вместо термина «функция распределения» используют термин «интегральная функция распределения». Производная от функции распределения вероятностей называется функцией плотности распределения вероятностей или плотностью вероятности:

.

Функция от распределения вероятностей выражается через плотность вероятности в виде интеграла: .

Вероятность попадания случайной величины в интервал равна приращению функции распределения вероятностей на этом интервале:

.

Задача 13.  Случайная величина Х задана функцией распределения вероятностей

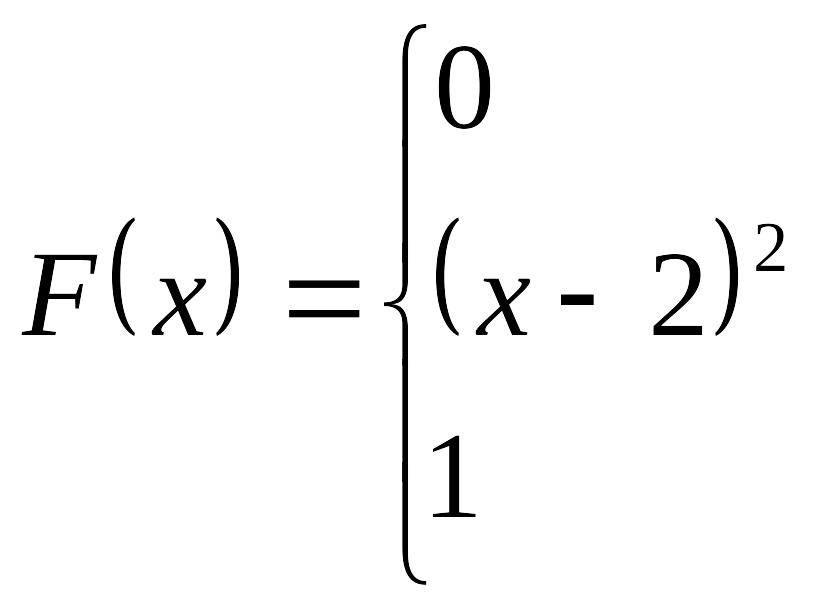
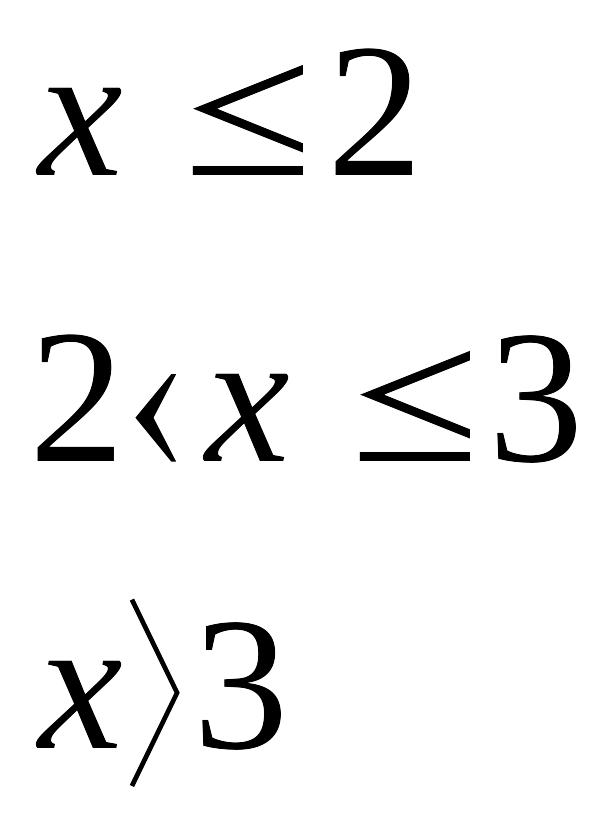
Найти плотность вероятности и вероятность попадания случайной величины Х в интервалы и .

Решение:

Т.к. , то

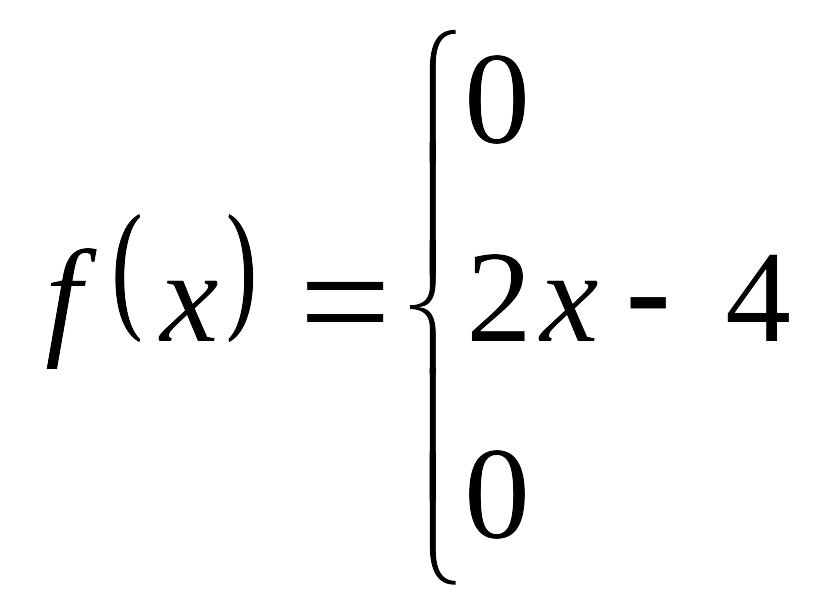
Вероятности попадания случайной величины Х в интервалы вычислим по формуле:

.

.

.

Задача 14.  Плотность вероятности непрерывной случайной величины

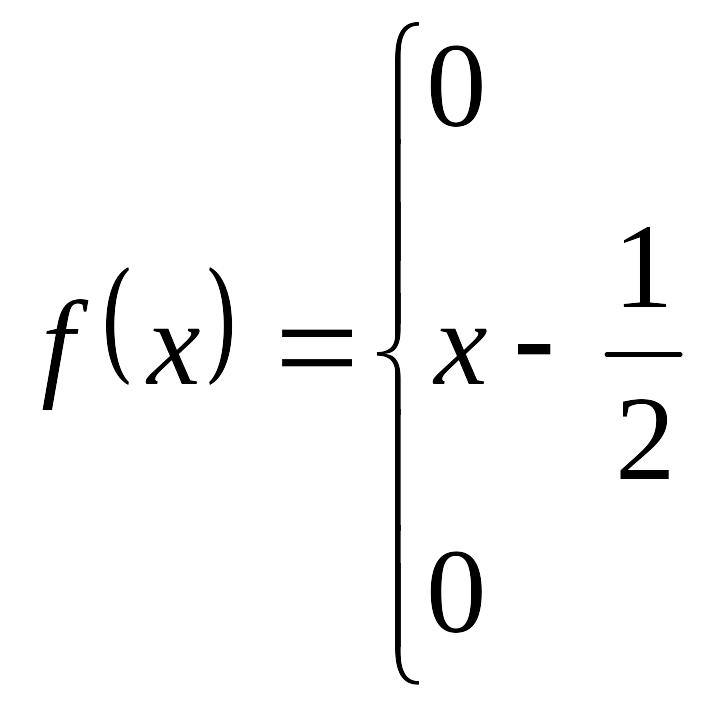
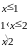
Найти функцию распределения и построить её график.

Решение:

, если

,

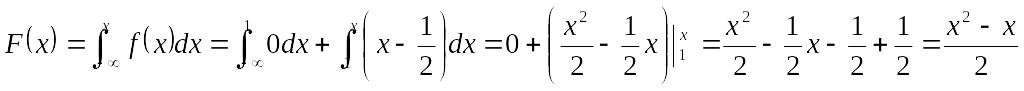если

,

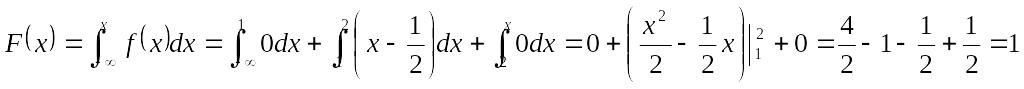если .

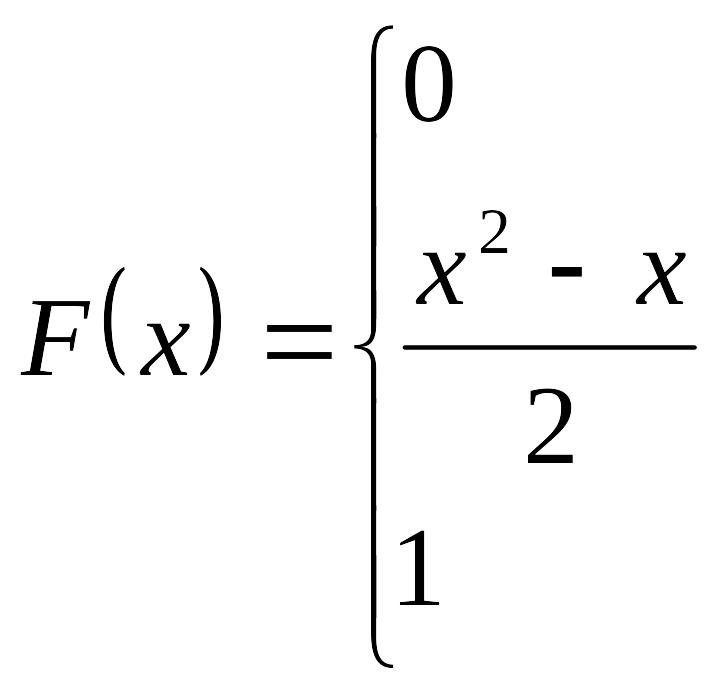
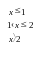
Построим график .

1

0,8

0,4

0,6

0,2

1,8

2,0

2,2

0

1

1,4б

1,6