
- •Математика
- •Введение
- •Студенты должны знать:
- •Приобрести практические навыки:
- •Содержание разделов дисциплины «Математика»
- •Раздел 1. Основы алгебры и анализа
- •Раздел 2. Интегральное исчисление. Обыкновенные дифференциальные уравнения. Ряды
- •Раздел 3. Теория вероятностей
- •Раздел 4. Численные методы и оптимизационные задачи
- •Контрольная работа № 1 включает задания по следующим темам:
- •Тема 1. Элементы линейной алгебры
- •Определители третьего порядка
- •Применение определителей к решению систем линейных уравнений
- •Решение систем линейных уравнений с – неизвестными
- •Рассмотрим решения типовых заданий по теме «Линейная алгебра»
- •Вопросы для самоконтроля по теме «Линейная алгебра»
- •Тема 2. Элементы аналитической геометрии Прямоугольная декартова система координат на плоскости
- •Кривые второго порядка
- •Вопросы для самоконтроля по теме «Аналитическая геометрия»
- •Тема 3. Введение в анализ Последовательность, предел последовательности
- •Предел функции
- •Основные теоремы о пределах функции
- •Некоторые приемы вычисления пределов функций
- •Имеем , тогда . Непрерывность функций
- •Вопросы для самоконтроля по теме «Введение в анализ»
- •Тема 4. Дифференциальное исчисление функции одной переменной Производная функции. Геометрический и механический смысл производной
- •Основные правила дифференцирования
- •Основные теоремы дифференциального исчисления
- •Возрастание и убывание функций
- •Экстремумы функции
- •Точки перегиба. Выпуклость и вогнутость
- •Асимптоты плоских кривых
- •Построение графиков функций
- •Вопросы для самоконтроля по теме «Дифференциальное исчисление функции одной переменной»
- •Тема 5. Дифференциальное исчисление функции нескольких переменных Функции нескольких переменных
- •Понятие предела для функции двух переменных
- •Определение: Градиентом функции называется вектор с координатами , в точке . По определению
- •Экстремумы функций нескольких переменных
- •Вопросы для самопроверки по теме «Дифференциальное исчисление функции нескольких переменных»
- •Тема 6. Неопределенный интеграл Первообразная функция и неопределенный интеграл
- •Простейшие свойства неопределенного интеграла
- •Основные приемы интегрирования
- •Общие приемы интегрирования
- •Интегрирование рациональных функций
- •Вопросы для самоконтроля по теме «Неопределенный интеграл»
- •Тема 7. Определенный интеграл
- •Формула Ньютона-Лейбница
- •Тема 8. Обыкновенные дифференциальные уравнения
- •Дифференциальное уравнение первого порядка
- •Уравнения с разделяющимися переменными
- •Однородные уравнения
- •Линейные уравнения
- •Уравнения -го порядка, допускающие понижение порядка
- •Линейные дифференциальные уравнения второго порядка с постоянными коэффициентами
- •Вопросы для самоконтроля по теме «Дифференциальные уравнения»
- •Тема 9. Ряды Общие сведения
- •Свойства рядов
- •Ряды с неотрицательными членами
- •Знакопеременные ряды
- •Степенные ряды. Интервал сходимости степенного ряда
- •Вопросы для самоконтроля по теме «Ряды»
- •Тема 10. Элементы Теории вероятностей Формулы комбинаторики
- •Совместные и несовместные события
- •Случайные величины
- •Числовые характеристики дискретной случайной величины
- •Непрерывные случайные величины
- •Математическое ожидание и дисперсия. Мода и медиана
- •Вопросы для самопроверки по теме «Теория вероятностей»
- •Тема 11. Комплексные числа Основные понятия
- •Вопросы для самоконтроля по теме «Комплексные числа»
- •Тема 12. Элементы линейного программирования Общая постановка задачи
- •Решение систем линейных неравенств с двумя переменными
- •Графический метод. Выбор оптимального варианта
- •Алгоритм симплексного метода
- •Транспортная задача
- •Метод потенциалов
- •Вопросы для самоконтроля по теме «Линейное программирование»
- •Контрольная работа № 1 (первый семестр)
- •Контрольная работа № 2 (второй семестр)
- •Контрольная работа № 3 (третий семестр)
- •Контрольная работа № 4 (четвертый семестр)
- •Методические указания по выполнению и оформлению контрольных работ
- •Формы и содержание отчетности студентов
- •Вопросы к экзамену (1 семестр)
- •Вопросы к зачету (2 семестр)
- •Вопросы к зачету (3 семестр)
- •Вопросы к экзамену (4 семестр)
- •Список литературы
- •Математика
- •1 62600, Череповец, ул. Сталеваров, 44
Экстремумы функции
Определение: Точка
![]() называется точкой максимума функции
на некотором промежутке
,
если существует такая окрестность точки
,
что для всех
этой окрестности выполняется неравенство
называется точкой максимума функции
на некотором промежутке
,
если существует такая окрестность точки
,
что для всех
этой окрестности выполняется неравенство
![]() .
Точка
называется точкой минимума функции
,
если существует такая окрестность точки
,
что для всех
этой окрестности выполняется неравенство
.
Точка
называется точкой минимума функции
,
если существует такая окрестность точки
,
что для всех
этой окрестности выполняется неравенство
![]() .
.
Точки максимума и минимума называются точками экстремума. Значение функции в точках максимума (минимума) называют максимумом (минимумом) функции, или экстремумом функции.
Необходимое условие экстремума дифференцируемой функции:
Если дифференцируемая
функция
имеет в точке
экстремум, то ![]() .
.
Достаточные условия существования экстремума кратко можно сформулировать так: если функция непрерывна в точке и в некоторой ее окрестности и ее производная при переходе через меняет знак с «+» на «-», то функция в точке имеет максимум; если же производная при переходе через точку меняет знак с минуса на плюс, то в точке функция имеет минимум.
Для нахождения экстремума функции нужно:
Найти точки, принадлежащие области определения функции , в которых ее производная
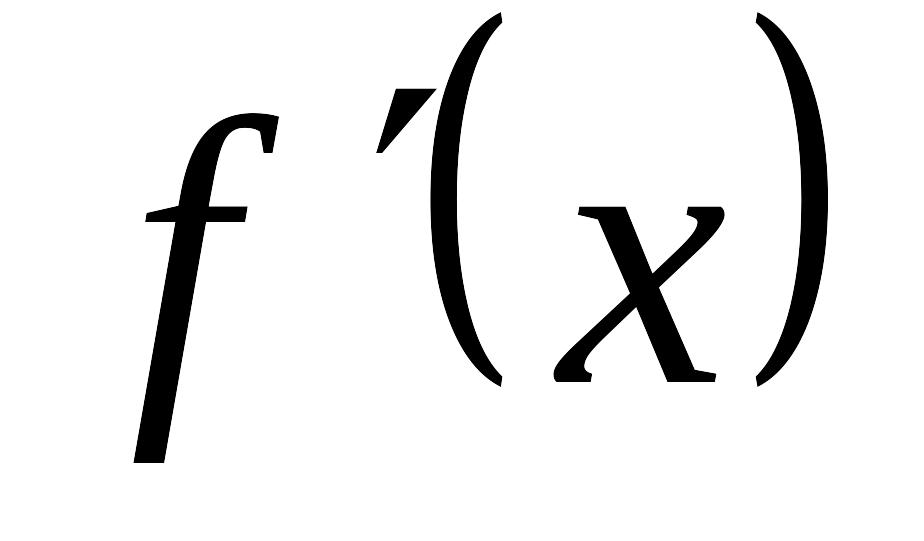 равна
или не существует, т.е. найти критические
точки функции по первой производной.
равна
или не существует, т.е. найти критические
точки функции по первой производной.Исследовать знак в некоторой окрестности каждой критической точки. При этом, если меняет знак при переходе через такую точку, то функция в этой точке имеет экстремум. Если же не меняется при переходе через рассматриваемую точку, то функция не имеет экстремума в этой точке.
Точки перегиба. Выпуклость и вогнутость
Пусть
в точке
кривая
имеет касательную, не параллельную
![]() .
.
Определение: Кривая называется выпуклой (вогнутой) в точке , если в некоторой окрестности этой точки кривая расположена ниже (выше) касательной, проведенной в точке .
Определение: Точка называется точкой перегиба кривой , если с одной стороны от кривая вогнута, а с другой стороны кривая выпукла.
Таким образом, если в точке кривая меняет выпуклость на вогнутость (или наоборот), то точка является точкой перегиба. Из этого определения непосредственно следует, что касательная в точке перегиба кривой пересекает эту кривую.
Для кривых можно сформулировать правила исследования на выпуклость, вогнутость и перегиб:
Находим точки, в которых
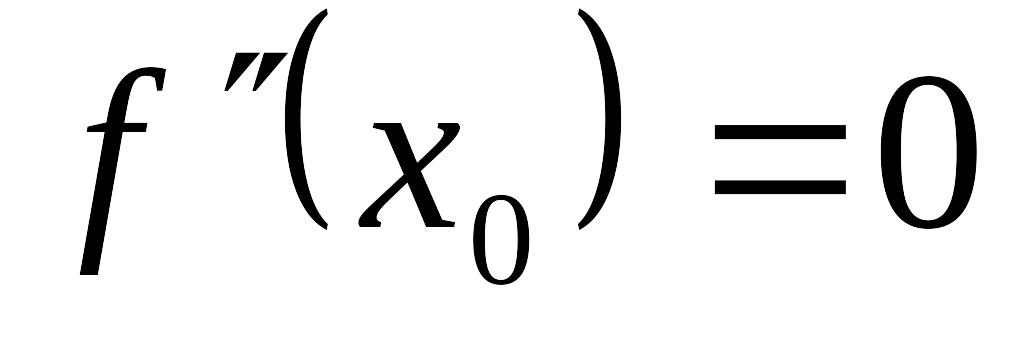 или вторая
производная функции
не существует. Такие точки называются
критическими точками функции
по второй производной.
или вторая
производная функции
не существует. Такие точки называются
критическими точками функции
по второй производной.Эти точки разделят область определения функции на интервалы, в каждом из которых
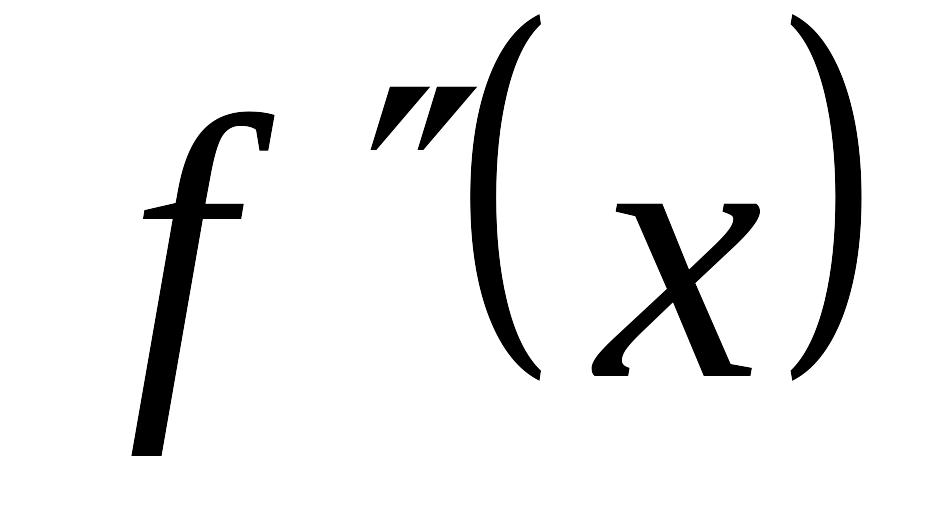 сохраняет знак.
сохраняет знак.
Если в рассматриваем
интервале
![]() ,
тот это интервал вогнутости, если же
,
тот это интервал вогнутости, если же
![]() ,
то это интервал выпуклости.
,
то это интервал выпуклости.
Точки перегиба выделяются автоматически: они разделяют интервалы выпуклости и вогнутости.
Асимптоты плоских кривых
Определение: Асимптотой кривой называется прямая, расстояние до которой от точки, лежащей на кривой, стремится к нулю при неограниченном удалении этой точки по кривой от начала координат или, что то же, когда расстояние точки от начала координат неограниченно растет.
Для того чтобы
кривая
имела асимптоту
![]() ,
необходимо и достаточно, чтобы
существовали конечные пределы
,
необходимо и достаточно, чтобы
существовали конечные пределы
![]() ,
,
![]() .
.
Если
![]() и
и
![]() –
конечно, то асимптота
–
конечно, то асимптота
![]() –
горизонтальная.
–
горизонтальная.
Определение:
Прямая
называется горизонтальной асимптотой,
если существует конечный предел при
![]() равный
,
т.е.
равный
,
т.е.
![]() .
.
Прямая
![]() ,
если
,
если
![]() .
.
Пример 1.
Найти асимптоты
кривой
![]() .
.
Область определения
функции
![]() ,
т.е.
,
т.е.
![]()
![]()
![]() – вертикальная
асимптота.
– вертикальная
асимптота.
Все остальные
асимптоты (если они есть) имеют вид
![]() .
Найдем
.
Найдем
![]() и
.
и
.
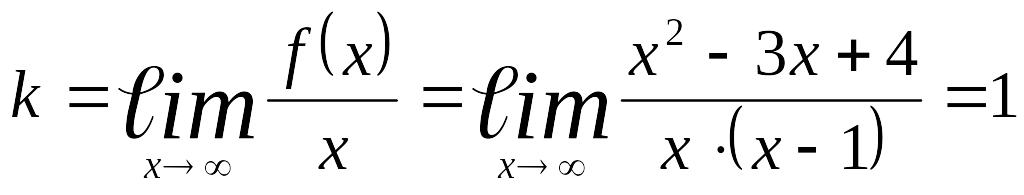 и
и
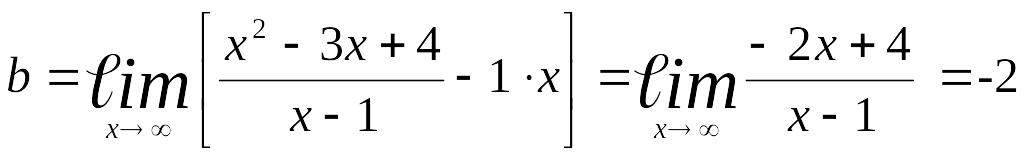 ,
,
![]() –
асимптота.
–
асимптота.
