
- •4.3 Требования к динамическому диапазону приемного тракта и технические решения, обеспечивающие их выполнение
- •4.3.1 Согласование динамических диапазонов элементов приемного тракта
- •4.3.2 Шумовая автоматическая регулировка усиления
- •4.3.3 Усилители с логарифмической амплитудной характеристикой
- •4.4 Технические решения, обеспечивающие помехозащиту рлс методами пространственной и поляризационной селекции
- •4.4.1 Уменьшение угловых размеров главного лепестка дна и снижение уровня боковых лепестков
- •4.4.2 Уменьшение уровня приема в направлении на постановщик ашп
- •4.5 Устройства защиты рлс от импульсных помех
- •4.5.1 Устройства защиты от узкополосных импульсных помех
- •4.5.2 Устройства защиты от широкополосных импульсных помех
- •4.5.3 Устройства защиты от нип
- •4.5.4 Особенности построения устройств защиты от ответных импульсных помех
- •4.6 Пути повышения помехозащищенности рлс в условиях пассивных помех
- •4.6.1 Основные отличия целей и маскирующих пассивных помех
- •4.6.2 Основные пути повышения помехозащищенности рлс
- •4.6.3 Выбор структуры зондирующего сигнала при работе рлс в условиях пассивных помех
- •4.7 Влияние пассивных помех на боевые возможности рлс
- •4.7.1 Методика определения возможностей рлс (рлк) по обнаружению воздушных объектов в условиях пассивных помех
- •4.8 Обобщенная структурная схема системы сдц
- •4.8.1 Структурная схема систем сдц
- •4.8.2 Основные характеристики системы сдц
- •4.9 Устройства селекции движущихся целей
- •4.9.1 Устройства сдц с эквивалентной внутренней когерентностью с чпв на видеочастоте
- •4.9.2 Устройства сдц с внешней когерентностью с чпв на видеочастоте
- •4.9.3 Устройства сдц с чпв на промежуточной частоте
- •4.10 Принципы построения элементов и устройств системы сдц
- •4.10.1 Ограничитель
- •4.10.2 Фазовый детектор
- •4.10.3 Устройство формирования опорного напряжения
- •4.10.4 Устройство череспериодной компенсации
- •4.10.5 Устройство чпк на вычитающих потенциалоскопах
- •4.10.6 Влияние нестабильностей аппаратуры на эффективность систем сдц
- •4.11 Системы сдц на базе автокомпенсаторов
- •4.11.1 Структурная схема чпак
- •4.11.2 Основные характеристики чпак
- •4.12 Фильтровые и корреляционно-фильтровые системы сдц
- •4.12.1 Фильтровые системы сдц
- •4.12.2 Корреляционно-фильтровые системы сдц
- •4.12.3 Основные характеристики фильтровых и корреляционнофильтровых систем сдц
- •4.13 Дискретно-аналоговые и цифровые системы сдц
- •4.13.1 Дискретно-аналоговые системы сдц
- •4.13.2 Цифровые системы сдц
- •5. Обработка радиолокационной информации
- •5.1 Первичная обработка радиолокационной информации
- •5.1.1 Задачи, решаемые при обработке рли
- •5.1.2 Сравнительная характеристика аналоговых и цифровых методов обработки
- •5.1.3 Обобщенная структурная схема системы цифровой обработки информации
- •5.2 Принципы построения устройств преобразования радиолокационных сигналов в цифровую форму
- •5.2.1 Устройства дискретизации аналоговых сигналов
- •5.2.2 Устройства квантования
- •5.2.3 Аналого-цифровые преобразователи, их параметры и основные типы
- •5.3 Принципы построения цифровых обнаружителей радиолокационных сигналов
- •5.3.1 Цифровые обнаружители радиолокационных сигналов при бинарном квантовании
- •5.3.2 Цифровые обнаружители радиолокационных сигналов при многоуровневом квантовании
- •5.4 Цифровые измерители координат воздушных объектов
- •5.4.1 Цифровые измерители дальности и азимута
- •5.4.2 Измерение доплеровской частоты сигнала
- •5.5 Вторичная обработка радиолокационной информации
- •5.5.1 Существо процедур вторичной обработки рли
- •5.5.2 Стробирование и селекция отметок в стробах
- •5.5.3 Оценка параметров траекторий
- •5.5.3.1 Сглаживание и экстраполяция при вторичной обработке
- •5.5.3.2 Алгоритм фильтрации параметров траектории по методу максимального правдоподобия
- •5.5.4 Оптимальное последовательное сглаживание координаты и скорости ее изменения
- •5.5.5 Последовательное сглаживание скорости и курса. Выявления маневра воздушного объекта
- •5.5.6 Обнаружение и сопровождение траекторий воздушных объектов в обзорной рлс
- •5.5.6.1 Структурная схема алгоритма обнаружения траекторий
- •5.5.6.2 Структурная схема алгоритма сопровождения траекторий
- •5.5.7 Полуавтоматическое сопровождение траекторий воздушных объектов
- •5.6 Радиолокационное распознавание
- •5.6.1 Классификация методов и показателей качества радиолокационного распознавания
- •5.6.2 Оценка вероятности правильного распознавания
- •5.6.3 Методы и техника радиолокационного распознавания
- •5.6.3.1 Методы радиолокационного распознавания
- •5.6.3.2 Техника распознавания, проблемы ее реализации
- •6. Дополнительные системы рлс
- •6.1 Индикаторные устройства рлс и их основные характеристики
- •6.1.1 Назначение и классификация индикаторных устройств
- •6.1.2 Влияние индикаторов на характеристики рлс
- •6.2 Принципы построения индикаторов обзорных рлс
- •6.2.1 Функциональный состав индикатора
- •6.2.2 Ико с вращающимися отклоняющими системами
- •6.2.3 Индикатор кругового обзора с неподвижной отклоняющей системой
- •6.3 Принципы построения системы отображения радиовысотомера
- •6.3.1 Способы построения индикаторов измерения высоты
- •6.3.2 Функциональная схема индикатора измерения высоты
- •6.4 Системы передачи и формирования масштабных отметок азимута рлс ртв
- •6.4.1 Принципы построения систем передачи азимута рлс ртв
- •6.4.2 Принципы построения систем формирования масштабных отметок азимута рлс ртв
- •6.5 Системы вращения антенн рлс ртв
- •6.5.1 Назначение, режимы работы, классификация систем вращения антенн и основные тактико-технические требования, предъявляемые к ним
- •6.5.2 Принципы построения основных типов систем вращения
- •7. Принципы построения и функционирования систем имитации, контроля и управления
- •7.1 Система имитации сигналов и помех. Общие сведения о системе имитации
- •7.1.1 Задачи решаемые системой имитации и ее роль в составе аппаратуры рлс
- •7.1.2 Требования, предъявляемые к имитатору и его основные особенности
- •7.1.3 Краткая характеристика имитируемых сигналов
- •7.2 Состав, структура и принципы функционирования имитатора
- •7.3 Блок имитации эхо-сигналов и активных помех (111-01). Назначение, состав, принцип работы
- •7.3.1 Назначение и состав блока
- •7.3.2 Фоpмиpователь сигналов ц1
- •7.3.3 Фоpмиpователь сигналов ц2
- •7.3.4 Формирователь шумовых помех гш2
- •7.3.5 Формирователь несинхронных и синусоидальных помех
- •7.3.6 Распределитель сигналов
- •7.4 Блок имитации пассивных помех (111-02). Назначение, состав, принцип работы
- •7.4.1 Имитатор отражений от облака дипольных помех (формирователь пп)
- •7.4.2 Имитатор отражений от местных предметов (формирователь мп)
- •7.5 Блок формирования контрольных сигналов (111-03). Назначение, состав, принцип работы
- •7.5.1 Назначение и состав блока
- •7.5.2 Формирователь шумовых помех гш1
- •7.5.3 Формирователь сигналов контрольной цели
- •7.5.4 Формирователь сигналов контрольного местного предмета
- •7.5.5 Устройство коммутации и распределения сигналов
- •7.5.6 Формирователи сигналов спл и фап
- •7.6 Вспомогательные блоки системы имитации. Назначение, принцип работы
- •7.6.1 Блок преобразования частоты (114-01)
- •7.6.2 Блоки фазовращателей (115-04, 115-05)
- •7.6.3 Блок управления имитатором (112-01)
- •7.6.4 Блок кодирования (072-03) и блок декодирования (072-04) команд управления фазовращателями
- •7.7 Система контроля. Общие сведения о системе контроля
- •7.7.1 Назначение и состав системы контроля
- •7.7.2 Режимы работы подсистемы автоматического контроля и диагностирования
- •7.7.3 Режим непрерывного контроля
- •7.7.4 Режим функционального контроля
- •7.7.5 Режим диагностического контроля
- •7.8 Аппаратура диагностирования
- •7.8.1 Принципы построения и функционирования аппаратуры диагностирования
- •7.8.2 Принципы построения и работы периферийных устройств контроля
- •7.8.3 Принципы построения блока диагностирования
- •7.9 Системы управления и сопряжения с внешними системами
- •7.9.1 Назначение, состав, принцип работы системы управления
- •7.9.2 Блок программного включения кабины пд (081-03). Назначение, принцип работы
- •7.9.3 Блок управления приемо-передающей аппаратурой (081-01). Назначение, принцип работы
- •7.9.4 Технический пульт управления (081-02). Назначение, принцип работы
- •7.10 Общие сведения о системе дистанционного управления
- •7.10.1 Назначение, состав и принцип работы системы дистанционного управления
- •7.10.2 Оперативный пульт управления рлс (071-01). Назначение, принцип работы
- •8. Перспективы развития радиоэлектронной техники ртв
- •8.1 Перспективные направления развития радиолокации
- •8.2 Перспективные направления развития систем и устройств радиолокационных станций ртв
- •Литература
- •Оглавление
5.6.2 Оценка вероятности правильного распознавания
Рассмотрим решение задачи распознавания целей по одному признаку Х (например, σц), когда объект может быть отнесен к одному из двух возможных классов: класс I – бомбардировщики, класс II -ракета.
Пусть признак класса I имеет плотность распределения вероятностей f1(X), а класса II – f2(X) (рис.5.37).

Рис.5.37. Вид плотностей распределения вероятностей
Выберем правило, согласно которому можно отнести цели к одному из классов по результату измерения признака.
По аналогии со случаем обнаружения одномерного сигнала таким правилом может быть сравнение измеренного значения Х с выбранным порогом Хo. Если X < Xo -цель относится к классу II, а если X > Xo – к классу I. Если X = Xo, то необходимо продолжать измерение признака X до тех пор, пока не будет принято решение о принадлежности цели к тому или иному классу.
При распознавании возможны ошибки: первого рода – цель класса II принята за цель класса I и второго рода – цель класса I принята за цель класса II. Условные вероятности этих ошибок определяются по следующим формулам (см.рис.5.37)
![]() (5.26)
(5.26)
![]() (5.27)
(5.27)
Для выбора порога Xo воспользуемся критерием минимума среднего риска
M [C] = C = C12 P(I*II) + C21 P(II*I), (5.28)
где C12 и C21 – стоимости ошибок первого и второго рода соответственно; P(I*II) и P(II*I) – вероятности ошибок первого и второго рода соответственно.
Заменяя P(I*II) = P(I*/II) P(II) и P(II*I) = P(II*/I) P(I), (5.29)
получим C = C12 P(II) P(I*/II) + C21 P(I)P(II*/I), (5.30)
или
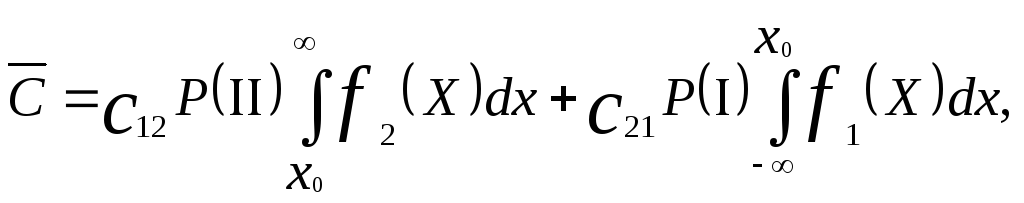 (5.31)
(5.31)
где P(I) и P(II) – априорные вероятности наличия в заданном пространстве целей I и II класса соответственно.
Для определения величины Xo, при которой С минимальна, продифференцируем С по Х и приравняем производную к нулю в точке Х = Xo
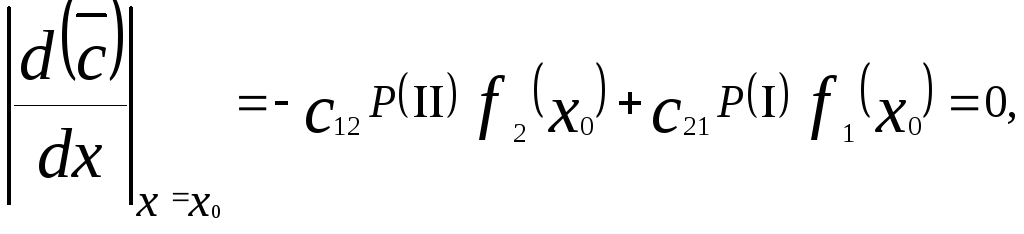 (5.32)
(5.32)
откуда
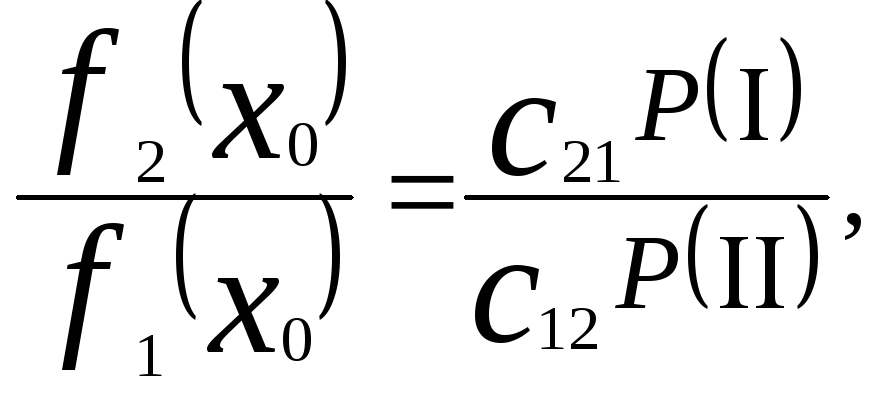 (5.33)
(5.33)
Приняв допущение о том, что P(I) = P(II), а C12 = C21 и признак Х имеет нормальный закон распределения, получим
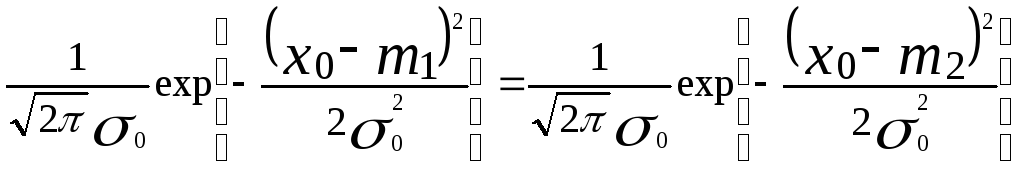
![]()
Решая уравнение относительно Xo, определим величину порога
Xo = 0,5 (m1 + m2), (5.35)
так как (Xo – m1)2 = (Xo – m2)2, 2Xo(m1 – m2)= m12 – m22, 2Xo(m1 – m2) = (m1 – m2)(m1 + m2) .
Для вычисления вероятности правильного распознавания необходимо определить вероятность попадания измеренного признака цели класса I в интервал от Xo до ∞ или признака цели класса II в интервал от – ∞ до Xo:
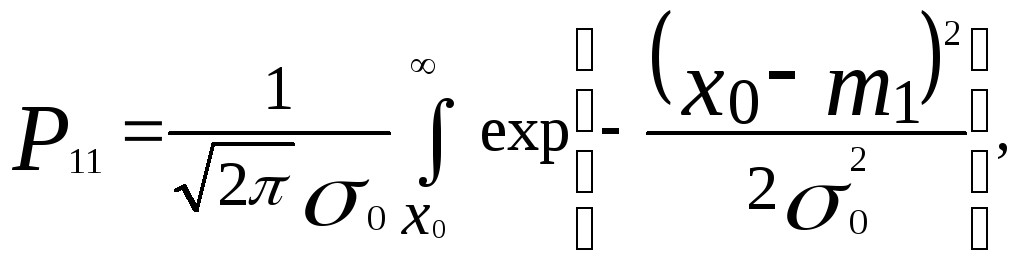 (5.36)
(5.36)
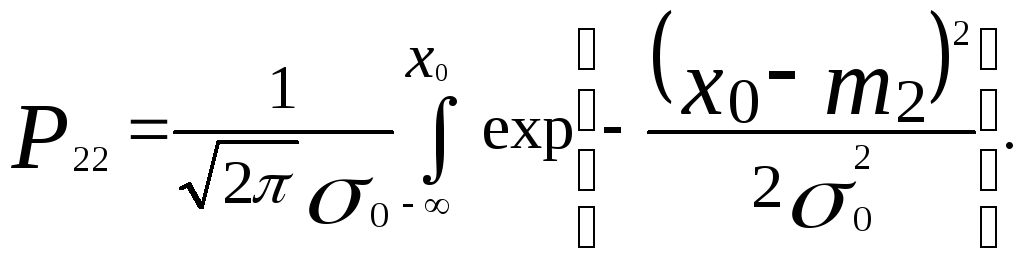 (5.37)
(5.37)
Произведя замену интегрирования (Xo – m1)/so = t и подставляя значение Xo = 0,5 (m1 + m2) получим:
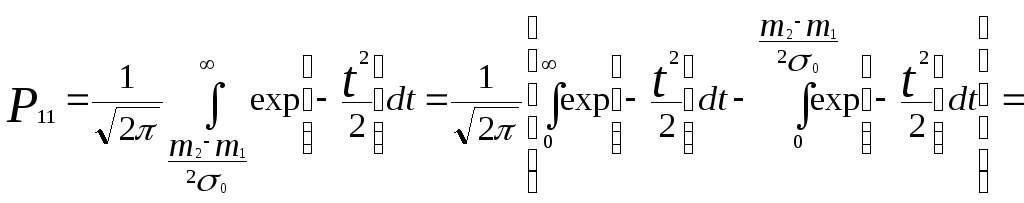
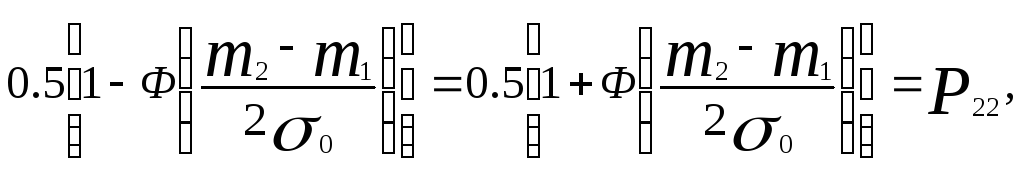
![]() (5.38)
(5.38)
Это выражение справедливо для случая, когда распознавание производится по одиночному измерению величины признака.
Если распознавание производится по результатам нескольких (n) измерений одного признака с квадратом ошибки каждого измерения σi2, то оценка истинного значения признака может производится по средневзвешенному значению измерений
![]()
В этом случае алгоритм распознавания принимает вид:
Если
 ,
то цель относится к классу Ι
,
то цель относится к классу Ι
Если
 ,
то цель относится к классу ΙΙ
,
то цель относится к классу ΙΙ
Если
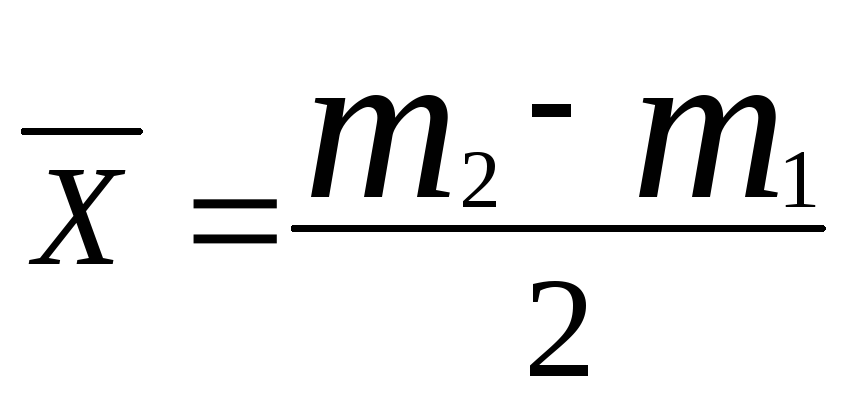 ,
то производится повторное измерение
,
то производится повторное измерение
При n – кратном и равноточном измерении одного признака, когда σ1 = σ2 =...= σn = σo дисперсия оценки признака равна
 (5.39)
(5.39)
Вероятность правильного распознавания в этом случае определяется по формуле:
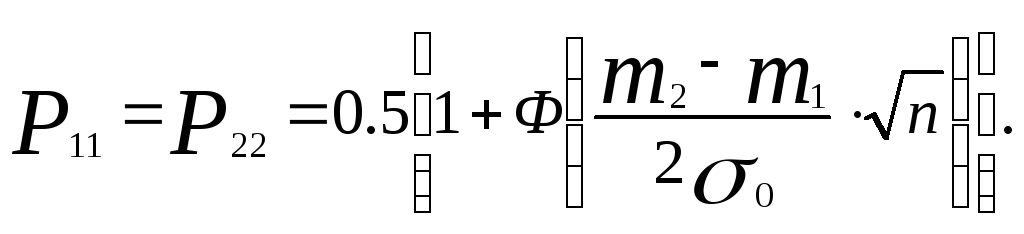 (5.40)
(5.40)
Из выражения (5.40) следует, чем больше количество измерений, тем выше вероятность распознавания.
Если распознавание осуществляется по к независимым признакам (ценности признаков равны), то вероятность правильного распознавания может быть определена по формуле
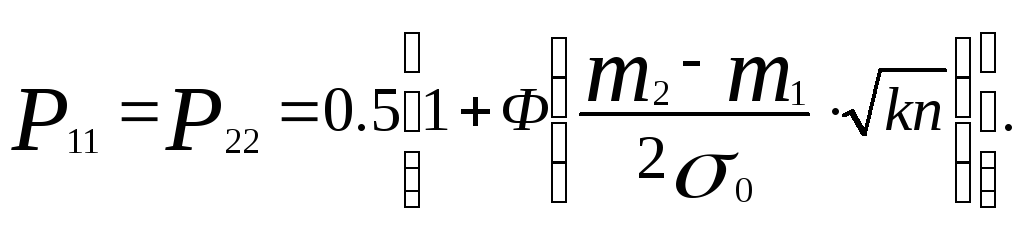 (5.41)
(5.41)
Из формулы (5.41) видно, что для независимых признаков одинаковой ценности (мощности) увеличение их количества равноценно увеличению числа измерений одного признака.
Таким образом, рассмотренная методика позволяет выбрать величину порога и оценить вероятность правильного распознавания.
