
- •4.3 Требования к динамическому диапазону приемного тракта и технические решения, обеспечивающие их выполнение
- •4.3.1 Согласование динамических диапазонов элементов приемного тракта
- •4.3.2 Шумовая автоматическая регулировка усиления
- •4.3.3 Усилители с логарифмической амплитудной характеристикой
- •4.4 Технические решения, обеспечивающие помехозащиту рлс методами пространственной и поляризационной селекции
- •4.4.1 Уменьшение угловых размеров главного лепестка дна и снижение уровня боковых лепестков
- •4.4.2 Уменьшение уровня приема в направлении на постановщик ашп
- •4.5 Устройства защиты рлс от импульсных помех
- •4.5.1 Устройства защиты от узкополосных импульсных помех
- •4.5.2 Устройства защиты от широкополосных импульсных помех
- •4.5.3 Устройства защиты от нип
- •4.5.4 Особенности построения устройств защиты от ответных импульсных помех
- •4.6 Пути повышения помехозащищенности рлс в условиях пассивных помех
- •4.6.1 Основные отличия целей и маскирующих пассивных помех
- •4.6.2 Основные пути повышения помехозащищенности рлс
- •4.6.3 Выбор структуры зондирующего сигнала при работе рлс в условиях пассивных помех
- •4.7 Влияние пассивных помех на боевые возможности рлс
- •4.7.1 Методика определения возможностей рлс (рлк) по обнаружению воздушных объектов в условиях пассивных помех
- •4.8 Обобщенная структурная схема системы сдц
- •4.8.1 Структурная схема систем сдц
- •4.8.2 Основные характеристики системы сдц
- •4.9 Устройства селекции движущихся целей
- •4.9.1 Устройства сдц с эквивалентной внутренней когерентностью с чпв на видеочастоте
- •4.9.2 Устройства сдц с внешней когерентностью с чпв на видеочастоте
- •4.9.3 Устройства сдц с чпв на промежуточной частоте
- •4.10 Принципы построения элементов и устройств системы сдц
- •4.10.1 Ограничитель
- •4.10.2 Фазовый детектор
- •4.10.3 Устройство формирования опорного напряжения
- •4.10.4 Устройство череспериодной компенсации
- •4.10.5 Устройство чпк на вычитающих потенциалоскопах
- •4.10.6 Влияние нестабильностей аппаратуры на эффективность систем сдц
- •4.11 Системы сдц на базе автокомпенсаторов
- •4.11.1 Структурная схема чпак
- •4.11.2 Основные характеристики чпак
- •4.12 Фильтровые и корреляционно-фильтровые системы сдц
- •4.12.1 Фильтровые системы сдц
- •4.12.2 Корреляционно-фильтровые системы сдц
- •4.12.3 Основные характеристики фильтровых и корреляционнофильтровых систем сдц
- •4.13 Дискретно-аналоговые и цифровые системы сдц
- •4.13.1 Дискретно-аналоговые системы сдц
- •4.13.2 Цифровые системы сдц
- •5. Обработка радиолокационной информации
- •5.1 Первичная обработка радиолокационной информации
- •5.1.1 Задачи, решаемые при обработке рли
- •5.1.2 Сравнительная характеристика аналоговых и цифровых методов обработки
- •5.1.3 Обобщенная структурная схема системы цифровой обработки информации
- •5.2 Принципы построения устройств преобразования радиолокационных сигналов в цифровую форму
- •5.2.1 Устройства дискретизации аналоговых сигналов
- •5.2.2 Устройства квантования
- •5.2.3 Аналого-цифровые преобразователи, их параметры и основные типы
- •5.3 Принципы построения цифровых обнаружителей радиолокационных сигналов
- •5.3.1 Цифровые обнаружители радиолокационных сигналов при бинарном квантовании
- •5.3.2 Цифровые обнаружители радиолокационных сигналов при многоуровневом квантовании
- •5.4 Цифровые измерители координат воздушных объектов
- •5.4.1 Цифровые измерители дальности и азимута
- •5.4.2 Измерение доплеровской частоты сигнала
- •5.5 Вторичная обработка радиолокационной информации
- •5.5.1 Существо процедур вторичной обработки рли
- •5.5.2 Стробирование и селекция отметок в стробах
- •5.5.3 Оценка параметров траекторий
- •5.5.3.1 Сглаживание и экстраполяция при вторичной обработке
- •5.5.3.2 Алгоритм фильтрации параметров траектории по методу максимального правдоподобия
- •5.5.4 Оптимальное последовательное сглаживание координаты и скорости ее изменения
- •5.5.5 Последовательное сглаживание скорости и курса. Выявления маневра воздушного объекта
- •5.5.6 Обнаружение и сопровождение траекторий воздушных объектов в обзорной рлс
- •5.5.6.1 Структурная схема алгоритма обнаружения траекторий
- •5.5.6.2 Структурная схема алгоритма сопровождения траекторий
- •5.5.7 Полуавтоматическое сопровождение траекторий воздушных объектов
- •5.6 Радиолокационное распознавание
- •5.6.1 Классификация методов и показателей качества радиолокационного распознавания
- •5.6.2 Оценка вероятности правильного распознавания
- •5.6.3 Методы и техника радиолокационного распознавания
- •5.6.3.1 Методы радиолокационного распознавания
- •5.6.3.2 Техника распознавания, проблемы ее реализации
- •6. Дополнительные системы рлс
- •6.1 Индикаторные устройства рлс и их основные характеристики
- •6.1.1 Назначение и классификация индикаторных устройств
- •6.1.2 Влияние индикаторов на характеристики рлс
- •6.2 Принципы построения индикаторов обзорных рлс
- •6.2.1 Функциональный состав индикатора
- •6.2.2 Ико с вращающимися отклоняющими системами
- •6.2.3 Индикатор кругового обзора с неподвижной отклоняющей системой
- •6.3 Принципы построения системы отображения радиовысотомера
- •6.3.1 Способы построения индикаторов измерения высоты
- •6.3.2 Функциональная схема индикатора измерения высоты
- •6.4 Системы передачи и формирования масштабных отметок азимута рлс ртв
- •6.4.1 Принципы построения систем передачи азимута рлс ртв
- •6.4.2 Принципы построения систем формирования масштабных отметок азимута рлс ртв
- •6.5 Системы вращения антенн рлс ртв
- •6.5.1 Назначение, режимы работы, классификация систем вращения антенн и основные тактико-технические требования, предъявляемые к ним
- •6.5.2 Принципы построения основных типов систем вращения
- •7. Принципы построения и функционирования систем имитации, контроля и управления
- •7.1 Система имитации сигналов и помех. Общие сведения о системе имитации
- •7.1.1 Задачи решаемые системой имитации и ее роль в составе аппаратуры рлс
- •7.1.2 Требования, предъявляемые к имитатору и его основные особенности
- •7.1.3 Краткая характеристика имитируемых сигналов
- •7.2 Состав, структура и принципы функционирования имитатора
- •7.3 Блок имитации эхо-сигналов и активных помех (111-01). Назначение, состав, принцип работы
- •7.3.1 Назначение и состав блока
- •7.3.2 Фоpмиpователь сигналов ц1
- •7.3.3 Фоpмиpователь сигналов ц2
- •7.3.4 Формирователь шумовых помех гш2
- •7.3.5 Формирователь несинхронных и синусоидальных помех
- •7.3.6 Распределитель сигналов
- •7.4 Блок имитации пассивных помех (111-02). Назначение, состав, принцип работы
- •7.4.1 Имитатор отражений от облака дипольных помех (формирователь пп)
- •7.4.2 Имитатор отражений от местных предметов (формирователь мп)
- •7.5 Блок формирования контрольных сигналов (111-03). Назначение, состав, принцип работы
- •7.5.1 Назначение и состав блока
- •7.5.2 Формирователь шумовых помех гш1
- •7.5.3 Формирователь сигналов контрольной цели
- •7.5.4 Формирователь сигналов контрольного местного предмета
- •7.5.5 Устройство коммутации и распределения сигналов
- •7.5.6 Формирователи сигналов спл и фап
- •7.6 Вспомогательные блоки системы имитации. Назначение, принцип работы
- •7.6.1 Блок преобразования частоты (114-01)
- •7.6.2 Блоки фазовращателей (115-04, 115-05)
- •7.6.3 Блок управления имитатором (112-01)
- •7.6.4 Блок кодирования (072-03) и блок декодирования (072-04) команд управления фазовращателями
- •7.7 Система контроля. Общие сведения о системе контроля
- •7.7.1 Назначение и состав системы контроля
- •7.7.2 Режимы работы подсистемы автоматического контроля и диагностирования
- •7.7.3 Режим непрерывного контроля
- •7.7.4 Режим функционального контроля
- •7.7.5 Режим диагностического контроля
- •7.8 Аппаратура диагностирования
- •7.8.1 Принципы построения и функционирования аппаратуры диагностирования
- •7.8.2 Принципы построения и работы периферийных устройств контроля
- •7.8.3 Принципы построения блока диагностирования
- •7.9 Системы управления и сопряжения с внешними системами
- •7.9.1 Назначение, состав, принцип работы системы управления
- •7.9.2 Блок программного включения кабины пд (081-03). Назначение, принцип работы
- •7.9.3 Блок управления приемо-передающей аппаратурой (081-01). Назначение, принцип работы
- •7.9.4 Технический пульт управления (081-02). Назначение, принцип работы
- •7.10 Общие сведения о системе дистанционного управления
- •7.10.1 Назначение, состав и принцип работы системы дистанционного управления
- •7.10.2 Оперативный пульт управления рлс (071-01). Назначение, принцип работы
- •8. Перспективы развития радиоэлектронной техники ртв
- •8.1 Перспективные направления развития радиолокации
- •8.2 Перспективные направления развития систем и устройств радиолокационных станций ртв
- •Литература
- •Оглавление
5.4.2 Измерение доплеровской частоты сигнала
В когерентно-импульсных РЛС для измерения доплеровской частоты применяются многоканальные фильтровые схемы (рис.5.22).
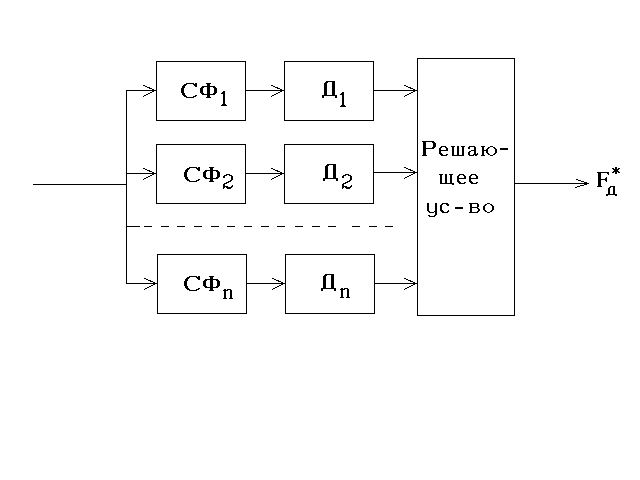
Рис.5.22. Многоканальная фильтровая схема для измерения доплеровской частоты
В такой схеме предусмотрено n частотных каналов с согласованными фильтрами, АЧХ которых перекрываются, и детекторами. Требуемое число каналов определяется по формуле
![]() (5.16)
(5.16)
где ΔFд макс – диапазон, подлежащий изменению доплеровской частоты, определяемый из известного соотношения
ΔFд макс = ± 2 Vr макс/ λ, (5.17)
δFд – разрешающая способность РЛС по доплеровской частоте, которая характеризуется протяженностью сечения тела неопределенности сигнала вдоль оси F.
Оценка Fд* грубо определяется по номеру канала с максимальной амплитудой выходного напряжения.
Для повышения точности оценивания используются выходные напряжения трех соседних частотных каналов с минимальным уровнем сигнала. В этом случае в качестве оценки принимается положение максимума параболической огибающей напряжений выбранных частотных каналов.
Реализация многоканальной схемы осуществляется в частотной области на основе дискретного преобразования Фурье. Анализатор спектра на основе ДПФ можно рассматривать как набор узкополосных фильтров, каждый из которых является согласованным для синусоидального сигнала с частотой, совпадающей с центральной частотой фильтра Fk = k/M·T (k = 0, 1, 2 ...N – 1), полоса пропускания каждого фильтра равна 1/M·T, где М – объем выборки.
Набор главных лепестков АЧХ анализатора спектра на основе ДПФ при М = 8 показан на рис.5.23.
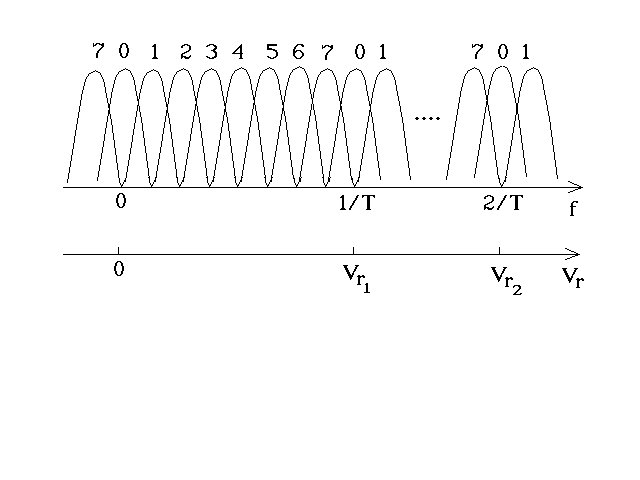
Рис.5.23. Набор главных лепестков АЧХ анализатора спектра на основе ДПФ
Обнаружение и оценка доплеровской частоты принимаемого сигнала производится по номеру канала ДПФ, в котором накопленный сигнал превысил порог обнаружения. Если порог обнаружения превышен в нескольких частотных каналах, производится усреднение или весовое объединение частотных оценок доплеровской частоты. Для ослабления влияния боковых лепестков в эквивалентах АЧХ фильтров используется специальные весовые функции. Дискретное преобразование Фурье при использовании весовой функции
![]()
где A(i) = A(iТ), (I = 0, 1, 2...., N – 1) – весовая функция.
Ошибка измерения Fд*. Максимальное значение ошибка примет в том случае, когда цель имеет такую Vr при которой средняя доплеровская частота колебаний попадает между фильтрами, а за оценку будет принято положение максимума одного из фильтров
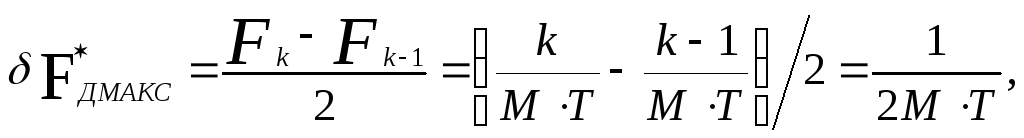 (5.18)
(5.18)
Учитывая, что значение Fд равновероятно распределению между соседними коэффициентами (фильтрами), то за счет дискретного характера отсчета
![]() (5.19)
(5.19)
Фазовый метод измерения радиальной скорости. Метод основан на измерении сдвига фаз сигнала за период посылки (через интервал времени Т) Δφ = ΏДΤ; где ΏД = ω·0·2Vr/c = 2π·Vr /λ = 2π·FД ;
 (5.20)
(5.20)
Из соотношения (5.20) находим
![]() (5.21)
(5.21)
Межпериодный сдвиг фаз Δφ можно определить на выходе фазового детектора в двух последовательных периодах зондирования
φi = arctg Yi/Xi ,
где i – номер зондирования, φi – фаза i-го импульса, Yi, Xi – квадратурные составляющие, т.е.
Δφ = φ2 – φ1.
Однако в силу стробоскопического эффекта по выходу фазового детектора изменения Vr будут неоднозначными с периодом неоднозначности, как следует из (5.21)
![]()
![]()
![]()
где n – номер интервала однозначности.
Для устранения неоднозначности необходимо иметь два независимых измерения одного и того же значения Vr полученных на шкалах с различными элементарными интервалами однозначности
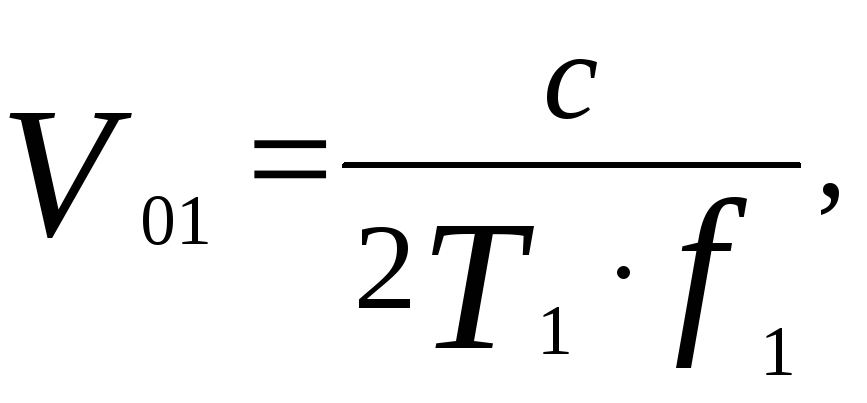
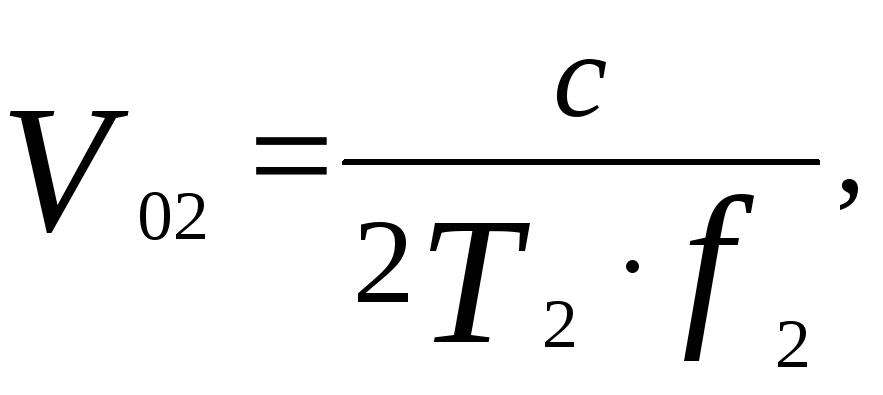
где Т1, Т2 – периоды следования импульсов, f1, f2 – несущая частота, с – скорость света.
В этом случае полный диапазон однозначных измерений Vr будет 1
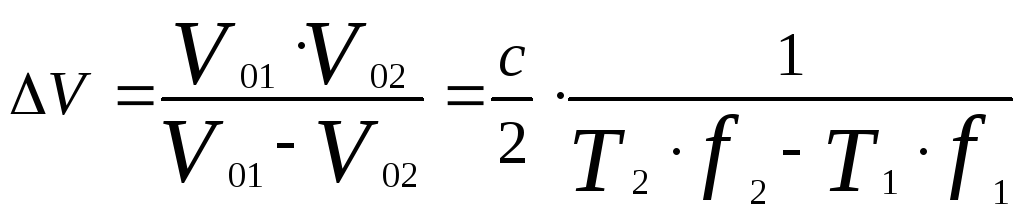 (5.22)
(5.22)
Если значения f2, Т2 определяются вобуляцией значений f1 и Т1,т.е.
f2 = f1 + Δf, Т2 = Т1 + ΔТ,
где Δf и ΔТ – соответственно глубина вобуляции несущей частоты и периода повторения, то формулу (5.22) можно записать в виде
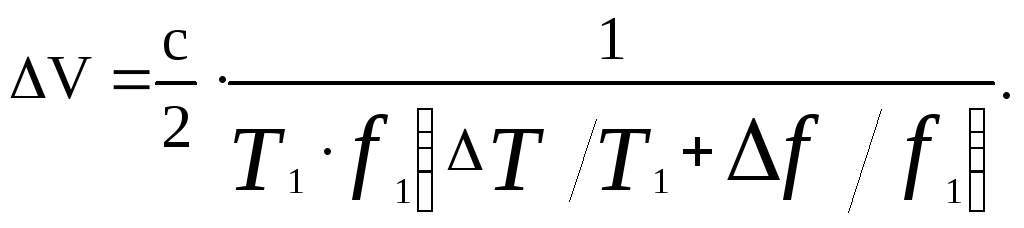
Таким образом, для обеспечения требуемого диапазона однозначного измерения Vr необходима вобуляция либо несущей частоты, либо периода повторения зондирующих сигналов, либо несущей и периода повторения одновременно. При этом вобуляция Т или f одинаково влияет на характеристики измерительной системы и в этом смысле эти виды вобуляции равноценны.
Обычно в алгоритме измерения Vr с устранением неоднозначности используется вобуляция только периода повторения импульсов. Период повторения выбирается при этом таким образом, чтобы обеспечить однозначное измерение дальности в соответствии с режимом обзора.
При практической реализации алгоритма измерения радиальной скорости Vr фазовым методом используют не менее 3-х шкал с различными элементарными интервалами однозначности. При этом значения периодов повторения Тi, Тj и разности этих периодов ΔТi,j для каждой пары шкал должны быть кратны, т.е. Тi/ΔТi,j и Тj/ΔТi,j должны быть величинами целыми.
Ошибки измерения радиальной скорости фазовым методом. Определяются ошибками 1-го и 2-го видов.
Ошибки 1-го вида, т.е. ошибки измерения неоднозначных значений Df (по-другому, ошибки при правильно устраненной неоднозначности) имеют непрерывный характер распределения со среднеквадратическим отклонением
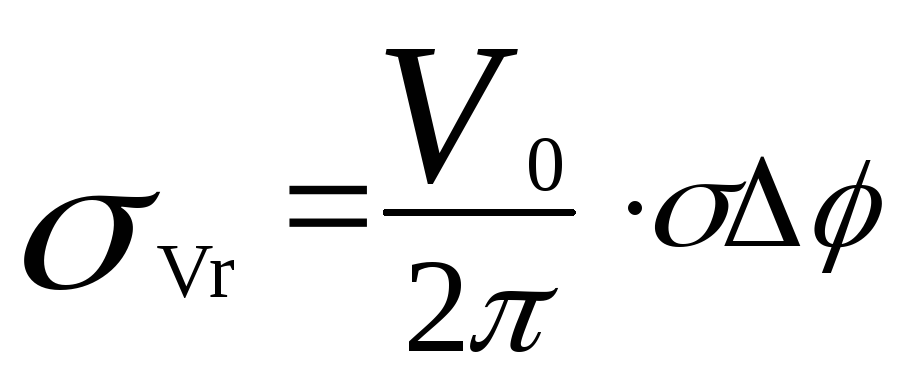 (5.23)
(5.23)
где Vo – элементарный интервал однозначности измерения Vr, σΔφ – ошибка измерения разности фаз.
Ошибки 2-го вида (аномальные ошибки) связаны с неверным устранением неоднозначности. Они имеют дискретное распределение, причем величина дискретности определяется величиной интервала однозначности.
При отношении сигнал/шум >3, распределение ошибок фазы смеси сигнала с шумом близко к нормальному с СКО σΔφ = 1/√q, где q – отношение с/ш по мощности. С учетом этого СКО измерения по одной из шкал
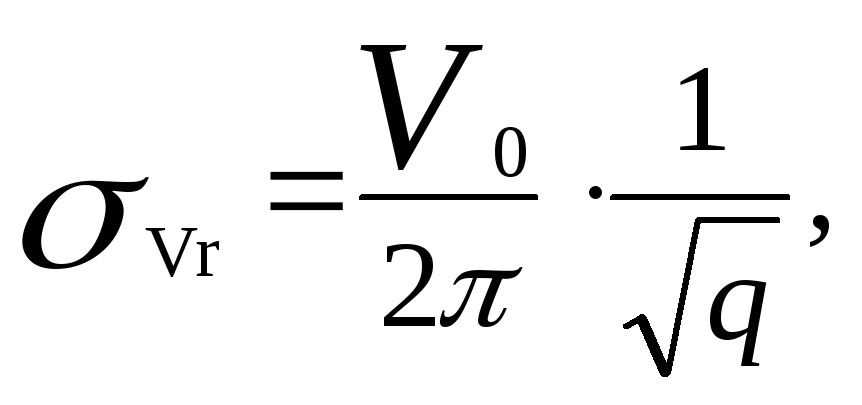 (5.24)
(5.24)
Таким образом, для уменьшения ошибок измерения при использовании фазового метода измерения радиальной скорости весьма важно иметь высокое отношение сигнал/шум.
