2.1. Понятие о матрицах Матрицейназывается прямоугольная таблица чисел следующего вида:

- элемент матрицы

(первый индекс – это номер строки, второй индекс – это номер столбца ; ). Размерность данной матрицы, а в общем виде –.

Матрица – это таблица и вычислить ее нельзя. Например, запасы тканей на конец года на базах Облпотребсоюза представлены в табл. 1.

Таблица 1. Запасы тканей на базах (тыс. грн.)

Базы Вид ткани	Донецкая	Артемовская	Мариупольская	Дружковская
Хлопчатобумажные	120,8	110,0	185,7	84,2
Шерстяные	41,3	13,0	60,0	18,4
Шелковые (натуральные)	15,7	0	0	12,3
Шелковые (искусственные)	21,8	12,0	40,0	15,0
Льняные	13,2	16,0	32,3	20,0

Здесь мы имеем матрицу размерности .

Матрица называется квадратной, если число строк равно числу столбцов (порядок матрицы). Матрица, состоящая из одной строки, называется матрицей-строкой. Матрица, состоящая из одного столбца, называется матрицей-столбцом.

Если в матрице поменять местами строки и столбцы, то эта операция называется транспонированием.

.

Матрица, все элементы которой равны 0, называется нуль - матрицей.

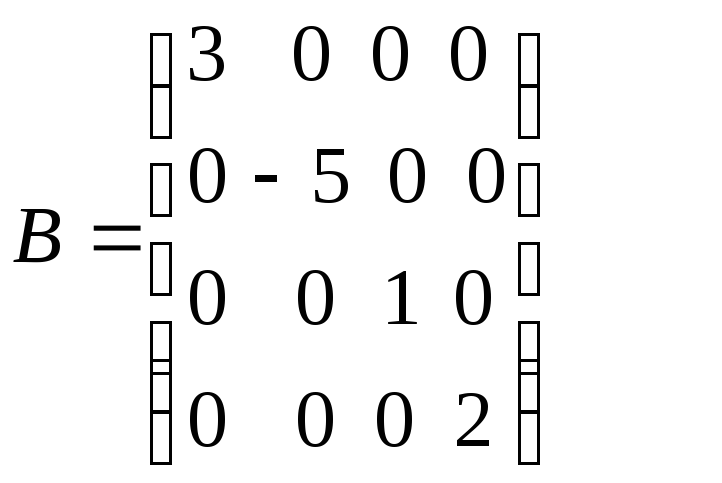
Квадратная матрица, у которой отличны от нуля лишь диагональные элементы, называется диагональной ( – диагональная матрица IV порядка).

.

Квадратная матрица называется единичной, если элементы главной диагонали равны 1, а все остальные – нули (это матрица ). Матрицы одной размерности считаютсяравными, если у них совпадают соответствующие элементы. Каждойквадратнойматрице можно поставить в соответствие определитель. Если определитель матрицы равен 0, то она называетсявырожденной, если определитель не равен 0, то матрица –невырожденная.

2.2. Действия над матрицами

1) Чтобы сложить матрицы одной размерности, нужно сложить их соответствующие элементы. По этому правилу формируют различные накопительные ведомости и таблицы.

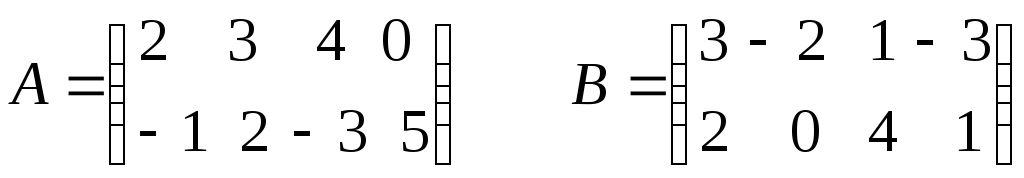
2) Чтобы матрицу умножить на число, необходимо на это число умножить все элементы матрицы. По этому правилу индексируют экономические показатели, приводя их в сопоставимый вид. Например, чтобы выразить запасы тканей в сопоставимых ценах, все значения умножают на индекс цен.

3) Чтобы из матрицы вычесть матрицу такой же размерности, необходимо произвести вычитание соответствующих элементов.

4) Операция умножения определяется не для любых двух матриц. Умножение матрицы на матрицу возможно, если число столбцов матрицы равно числу строк матрицы .

Пусть количество элементов в строках матрицы равно количеству элементов в столбцах матрицы :

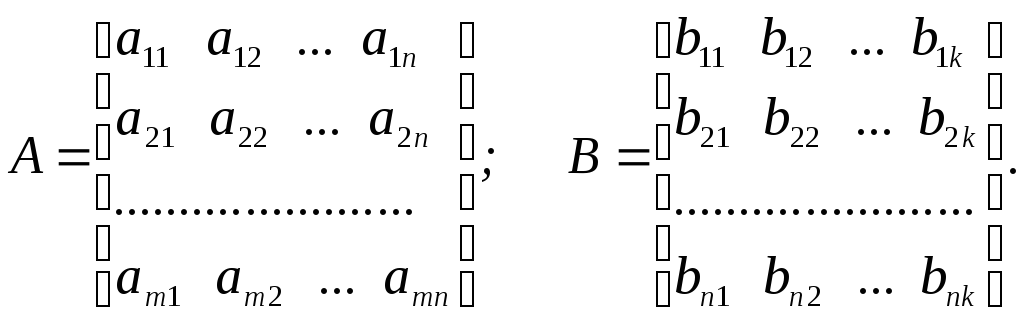
Такие матрицы называются соответственными (согласованными). Их можно перемножать.

Произведением матрицы на матрицу называется матрица

,

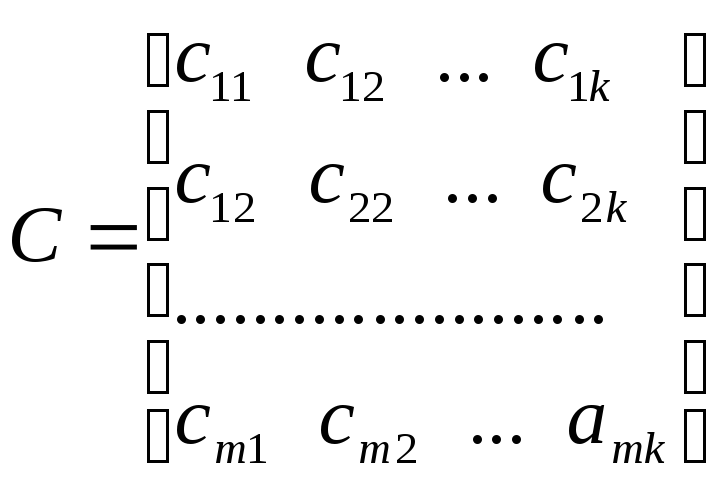где .

Таким образом, в результате умножения матрицы на матрицу получаем матрицу , число строк в которой равно числу строк матрицы , а число столбцов матрицы равно числу столбцов матрицы .

Другими словами, умножение матриц следует проводить очень внимательно, т.к. необходимо каждую строку матрицы умножить на каждый столбец матрицы по правилу скалярного произведения векторов.

Умножение матриц записывается так: . Произведение матриц может быть нуль-матрицей, хотя оба сомножителя не являются нуль-матрицами.

Умножение матриц обладает следующими свойствами.

а) Умножение матриц в общем случае некоммутативно: . (Если матрицы и обладают свойством , то говорят, что они перестановочны или что они коммутируют.) Свойством коммутативности обладает единичная матрица, т.е. , где – квадратная матрица.

б) Умножение матриц ассоциативно: .

в) Умножение матриц дистрибутивно относительно сложения:

.

г) Для умножения матриц справедливо равенство

д) Для транспонирования произведения матриц справедлива формула

е) Определитель произведения двух квадратных матриц одинакового порядка равен произведению их определителей:

.

Пример 7. Выполнить умножение матриц:

.

5) Обратной матрицей для называется матрица , которая при умножении на заданную матрицу дает единичную матрицу:

При нахождении обратной матрицы необходимо учитывать такие предпосылки:

а) обратная матрица существует только для квадратных матриц;

б) для существования обратной матрицы необходимо и достаточно, чтобы определитель заданной матрицы был отличен от нуля.

Рассмотрим матрицу третьего порядка

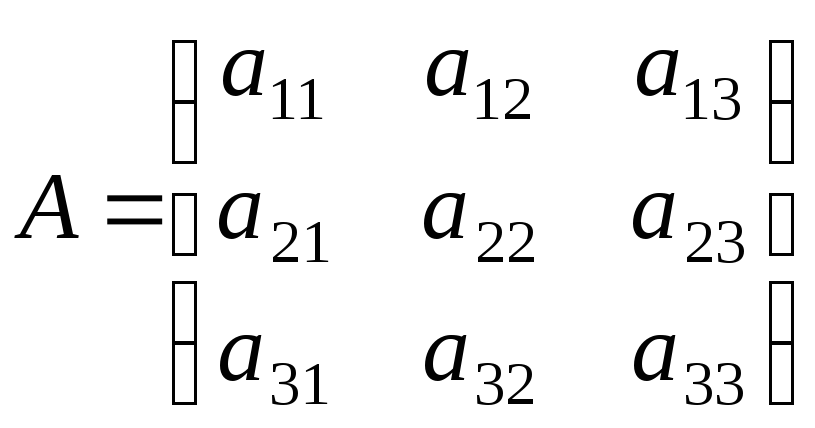
Будем предполагать, что она невырожденная, т.е. ее определитель не равен нулю. Каждому элементу соответствует алгебраическое дополнение .

Обратная матрица равна транспонированной матрице алгебраических дополнений, деленных на определитель матрицы.

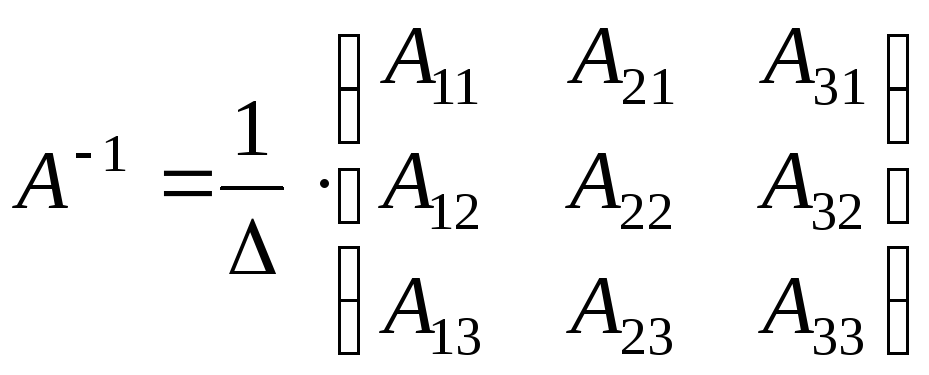
Пример 8. Найти обратную к следующей матрице.

Определитель матрицы

Найдем алгебраические дополнения

Следовательно, можно сформировать обратную матрицу:

.

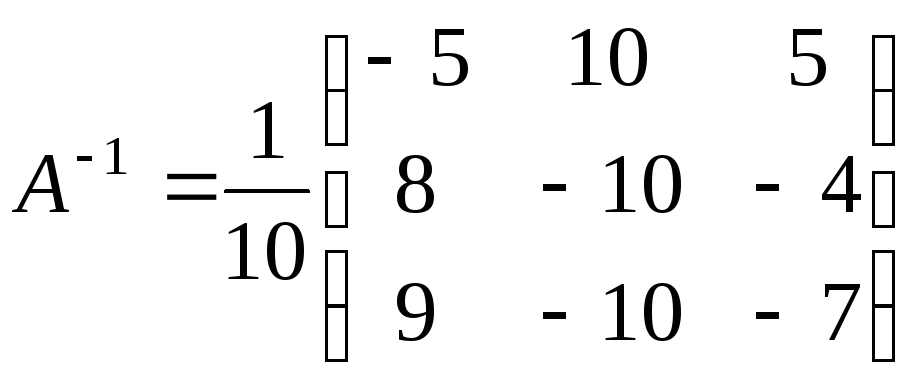Легко проверить, что

.

Значит, обратная матрица найдена верно.