3. Вопросы совместимости линейных уравнений

3.1. Ранг матрицы Рангом матрицы называется наивысший порядок отличного от нуля определителя, который можно образовать из элементов данной матрицы, сохраняя порядок следования элементов.

Из этого определения следует, что ранг имеет любая матрица. Если все элементы матрицы равны нулю, то и ранг ее равен нулю. Ранг матрицы будет равен единице, если имеется хоть один ненулевой элемент, а определители любого порядка, начиная со второго, все равны нулю. Из определения также вытекает, что необходимо вычислять все определители разных порядков. Например, если задана матрица пятого порядка, то для нахождения ранга следует вычислять определитель пятого порядка – он единственный. Если он отличен от нуля, то ранг равен 5. Если же он равен нулю, то следует вычислять определители четвертого порядка – их всего 25. Когда среди них встретится ненулевой, то процесс останавливается, и ранг равен 4. Если же все определители четвертого порядка равны нулю, переходят к определителям третьего порядка и т.д. Такая процедура оказывается долгой и трудоемкой, но в ней и нет нужды, если воспользоваться теоремой:

Теорема.

Ранг матрицы не меняется, если к ней применить элементарные преобразования, основанные на свойствах.

Используя элементарные преобразования, можно матрицу привести к треугольному виду, когда ниже главной диагонали будут располагаться нули. Число ненулевых диагональных элементов треугольного вида матрицы дает величину ранга .

Пример 12. Установить ранг матрицы.

~ ~

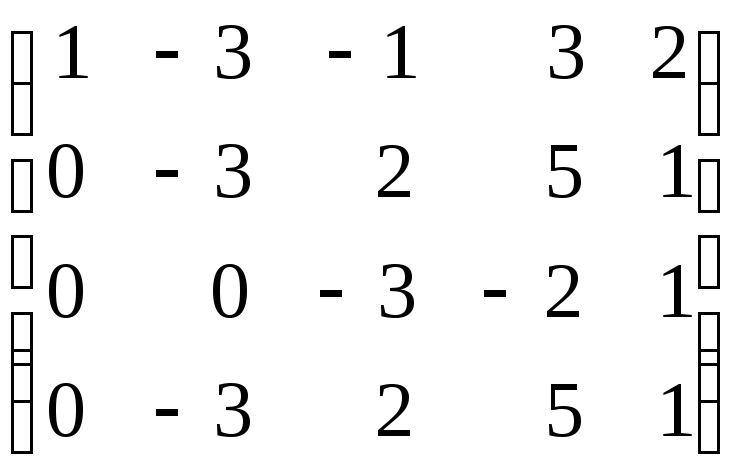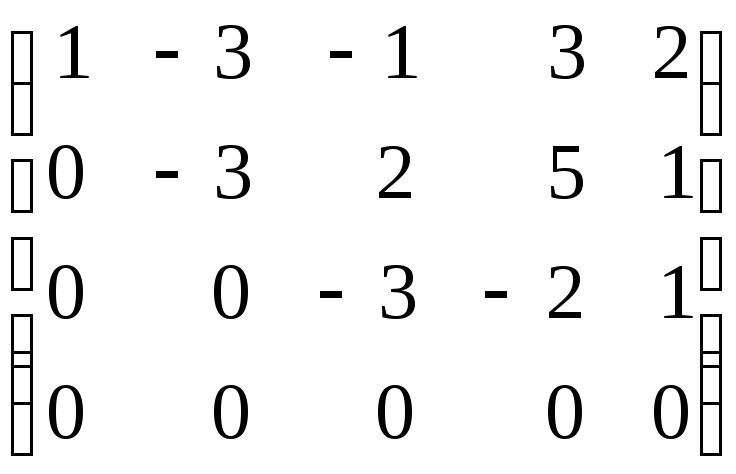
Пояснения:

1. матрица имеет размерность 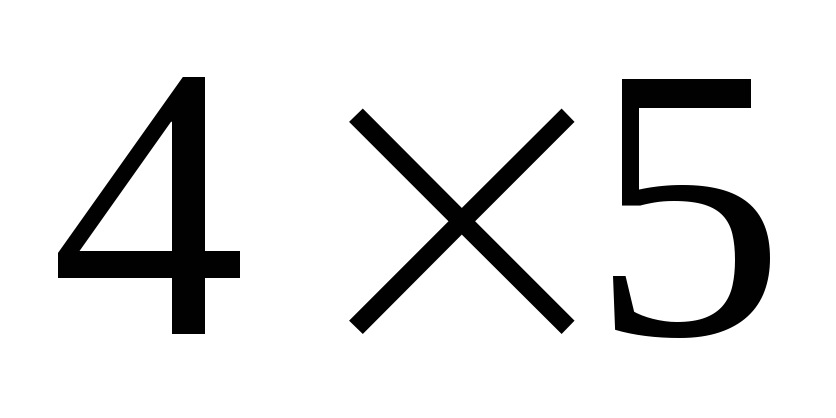, поэтому ранг не может быть больше 4;

2. с помощью первой строки получаем нули в первом столбце по правилу прямоугольника;

3. вычитаем из четвертой строки вторую. Видим, что четвертая строка состоит из нулей, ее можно отбросить. На главной диагонали находится три ненулевых элемента – ранг .

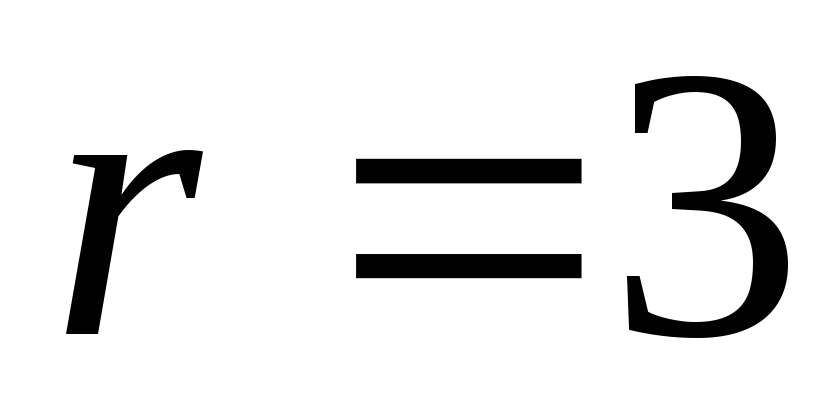Понятие ранга связано с понятием линейной независимости. Строки (столбцы) матрицы называются независимыми, если ни одна из них не может быть выражена линейно через другие. В противном случае они линейно зависимы.

Теорема.

Если ранг матрицы равен , то существует линейно независимых строк (столбцов), от которых линейно зависят все остальные строки (столбцы).

Из теоремы следует, что число линейно независимых строк совпадает с числом линейно независимых столбцов и равно рангу.

Пример 13. Показать, что функции

,

,

образуют линейно независимую систему.

Составим матрицу коэффициентов функций и найдем ее ранг

~ ~

Матрица приведена к треугольному виду, ее ранг равен 3. (Можно было вычислить , значит, ). Следовательно, функции линейно независимы.

3.2. Системы линейных неоднородных уравнений

Пусть дана произвольная система линейных уравнений:

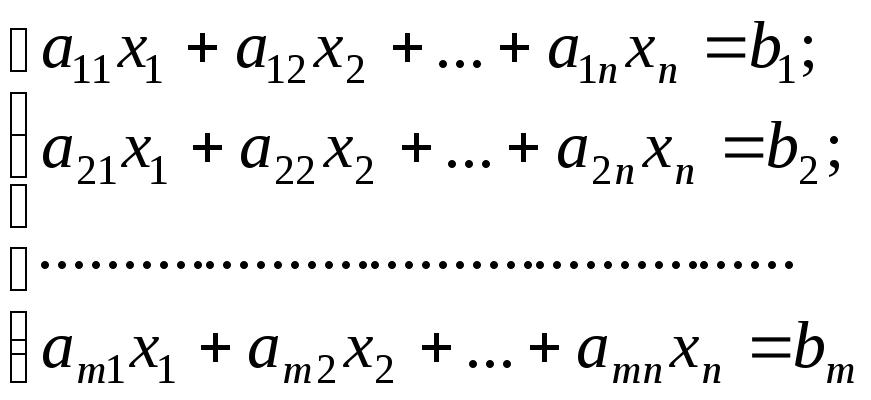
Обозначим через матрицу, составленную из коэффициентов при неизвестных системы, а через – матрицу, полученную из присоединением столбца свободных членов:

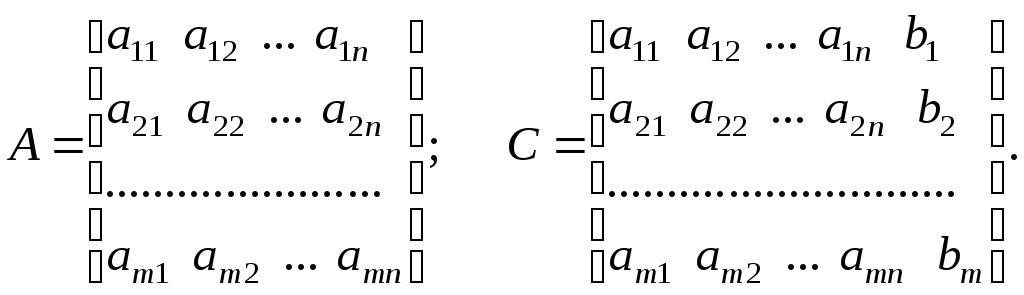
Матрица называетсяматрицей системы уравнений, а матрица –расширенной матрицейэтой системы.

Теорема Кронекера-Капелли. Для того чтобы система линейных уравнений быласовместна, необходимо и достаточно, чтобы ранг ее матрицы равнялся рангу расширенной матрицы . Если ранг матрицы равен рангу матрицы и равен числу неизвестных, то система имеет единственное решение. Если ранг матрицы равен рангу матрицы , но меньше числа неизвестных, то система имеет бесконечное множество различных решений.

Замечание. При исследовании на совместность системы линейных уравнений иногда удобнее начинать с вычисления ранга расширенной матрицы, тогда попутно легко установить и ранг матрицы.

Пример14. Установить совместность системы уравнений и число решений:

Составим расширенную матрицу и, пользуясь правилом прямоугольника, найдем ранг

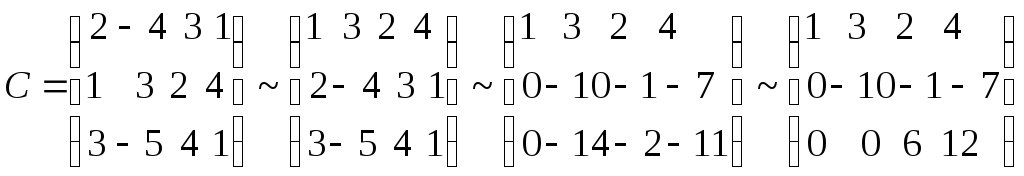
Ранг матрицы системы равен рангу расширенной матрицы – значит, система линейных уравнений совместна. Поскольку ранг равен числу переменных, то система имеет единственное решение – оно было найдено раньше с помощью метода Гаусса.

Пример 15.Проверить, совместна ли система уравнений и каким будет решение.

.

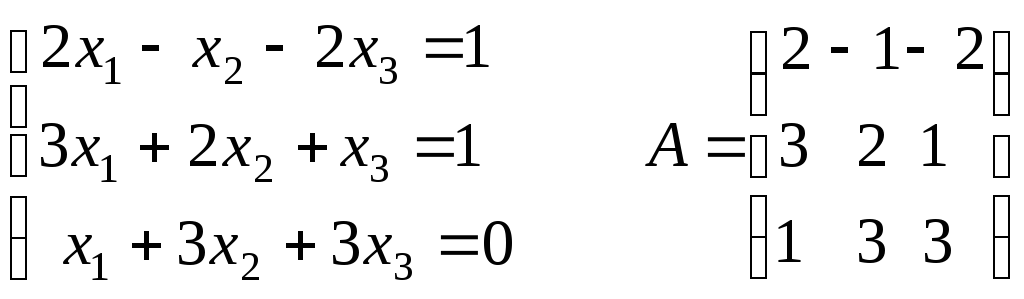
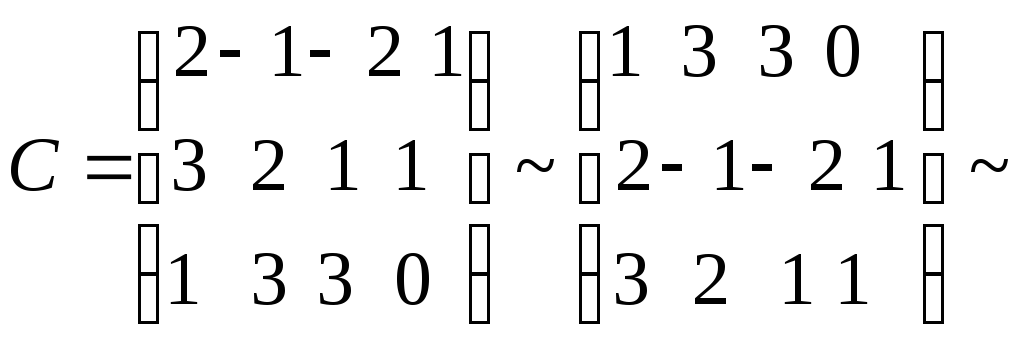
Система уравнений совместна, а т.к. ранг меньше числа переменных, то она имеет бесчисленное множество решений. Оставим первые два линейно независимых уравнения и перенесем слагаемое с в правую часть (называется свободной переменной).

Решаем по правилу Крамера

;

.

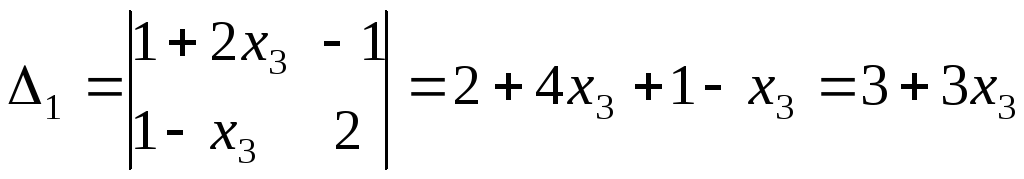
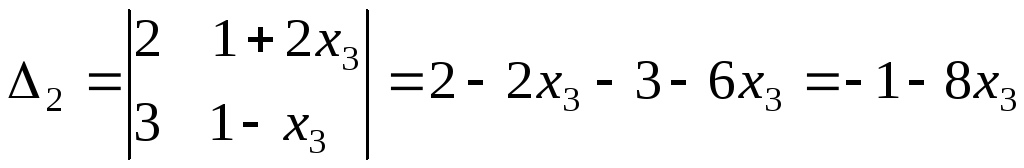Задавая любые значения , будем получать множество значений и . Например, пусть, тогда. Или пусть ,.