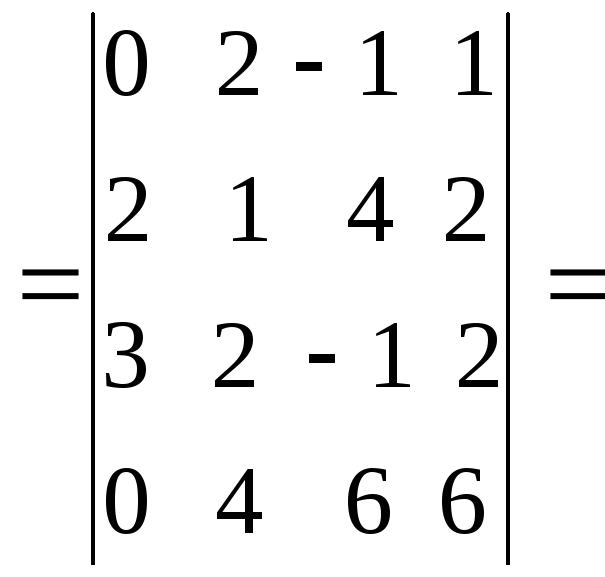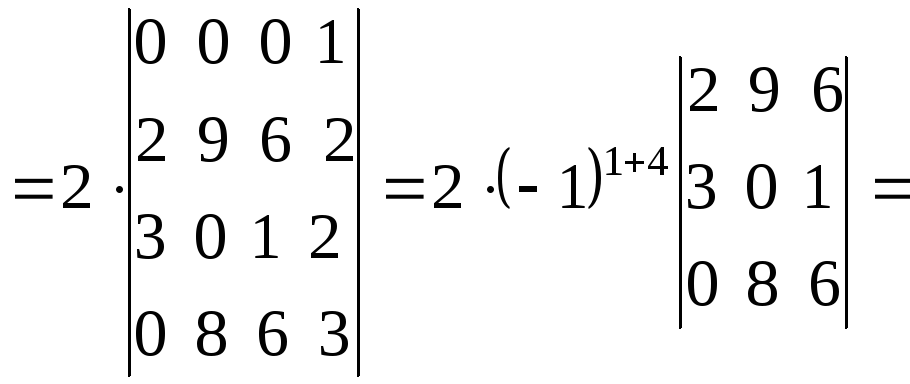1. Определители и системы линейных уравнений

1.1. Системы двух линейных уравнений и определители второго порядка

Рассмотрим систему двух линейных уравнений с двумя неизвестными:

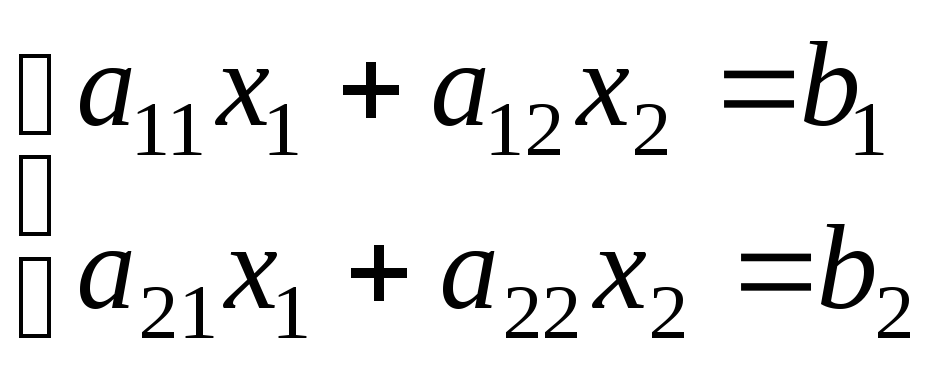
Коэффициенты при неизвестных и имеют два индекса: первый указывает номер уравнения, второй – номер переменной.

Главным определителем системы называется таблица, составленная из коэффициентов при неизвестных и заключенная в прямые скобки:

Вспомогательным определителем называют определитель, полученный из главного определителя заменой одного из столбцов на столбец свободных членов:

Главнаядиагональ определителя – это диагональ, направленная из левого верхнего угла в правый нижний угол. Вторая диагональ называетсяпобочной.

Определитель второго порядка равен разности между произведением элементов главной диагонали и произведением элементов побочной диагонали:

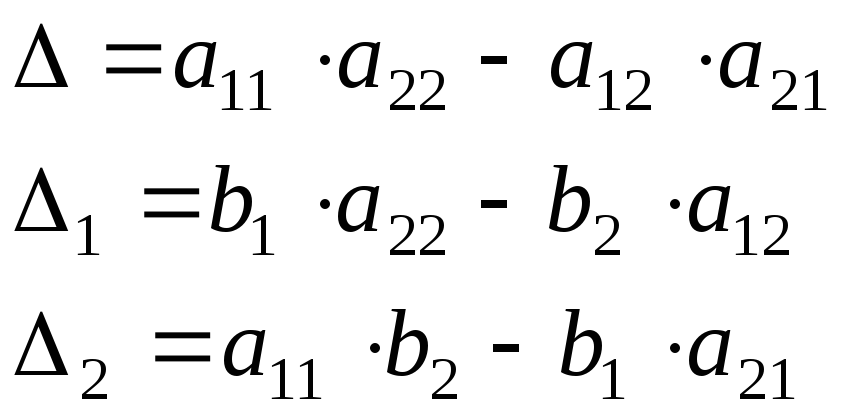
Правило Крамера: Решение системы находят путем деления вспомогательных определителей на главный определитель системы

,

Замечание 1.Использование правила Крамера возможно, если определитель системы не равен нулю.

Замечание 2.Формулы Крамера обобщаются и на системы большего порядка.

Пример 1. Решить систему: .

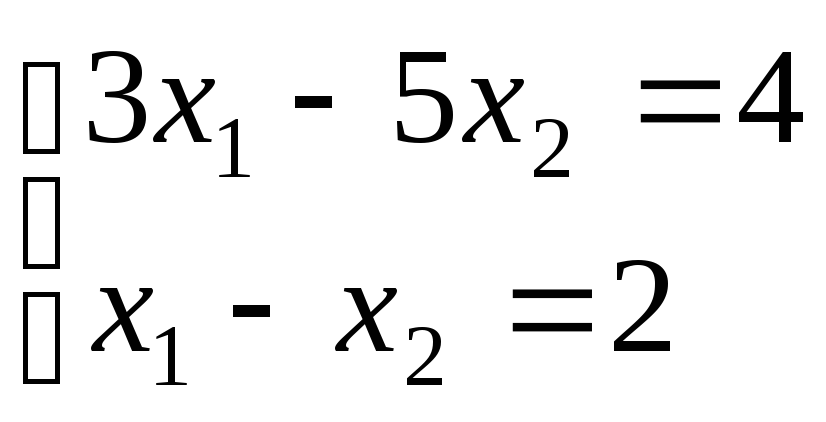Решение.

; ;

;

Проверка:

Вывод: Система решена верно: .

1.2. Системы трех линейных уравнений и определители третьего порядка

Рассмотрим систему трех линейных уравнений с тремя неизвестными:

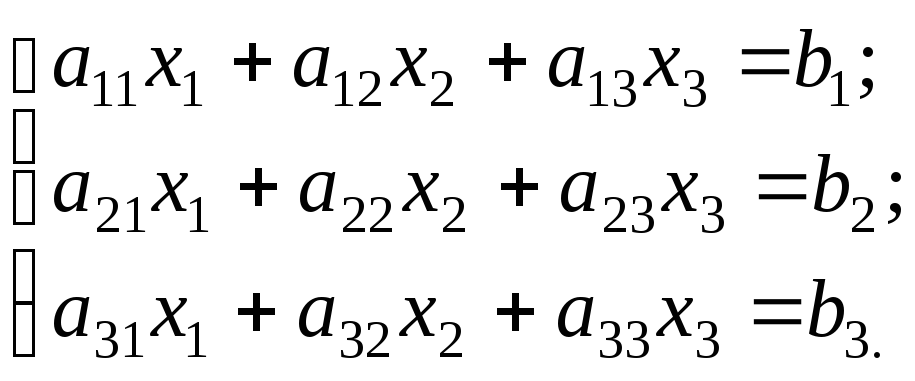
Определитель, составленный из коэффициентов при неизвестных, называется определителем системы или главным определителем:

.

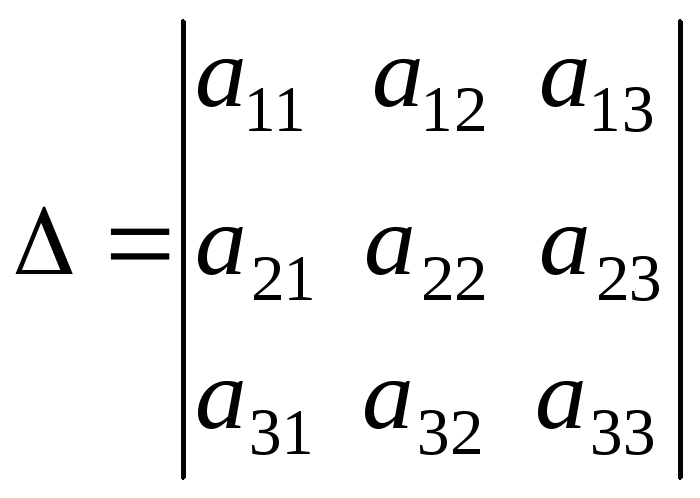Если то система имеет единственное решение, которое определяется по формулам Крамера:

где

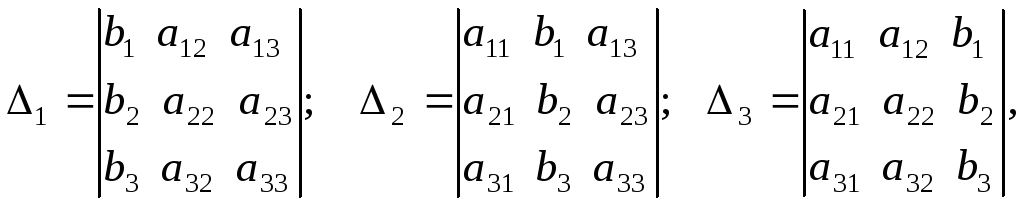
где определители – называются вспомогательными и получаются из определителя путем замены его первого, второго или третьего столбца столбцом свободных членов системы.

Пример 2.Решить систему .

Сформируем главный и вспомогательные определители:

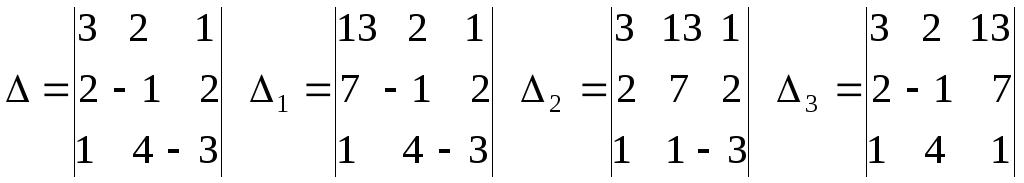
Осталось рассмотреть правила вычисления определителей третьего порядка. Их три: правило дописывания столбцов, правило Саррюса, правило разложения.

а) Правило дописывания первых двух столбцов к основному определителю:

.

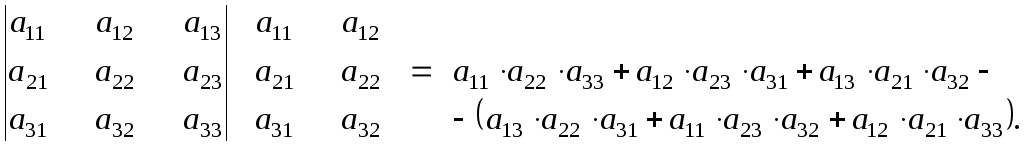
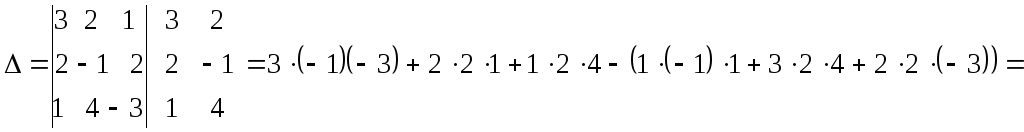
Вычисление проводятся следующим образом: со своим знаком идут произведения элементов главной диагонали и по параллелям к ней, с обратным знаком берут произведения элементов побочной диагонали и по параллелям к ней.

б) Правило Саррюса:

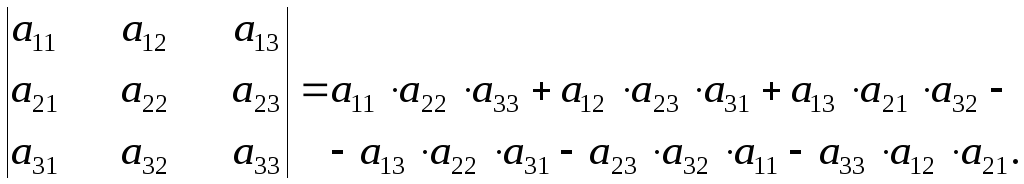
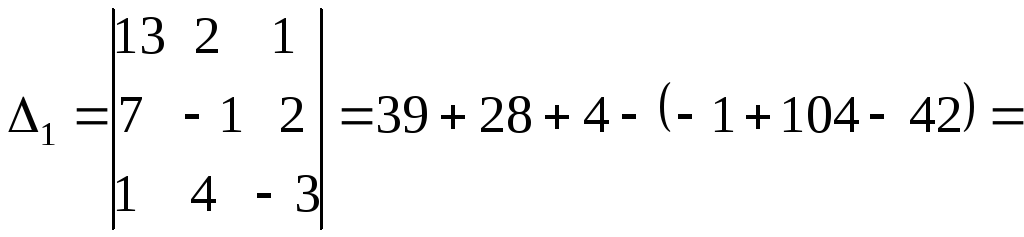
Со своим знаком берут произведения элементов главной диагонали и по параллелям к ней, причем недостающий третий элемент берут из противоположного угла. С обратным знаком берут произведения элементов побочной диагонали и по параллелям к ней, третий элемент берут из противоположного угла.

в) Правило разложения по элементам строки или столбца:

Определитель равен сумме произведений элементов какой-нибудь строки (столбца) на их соответствующие алгебраические дополнения.

Если 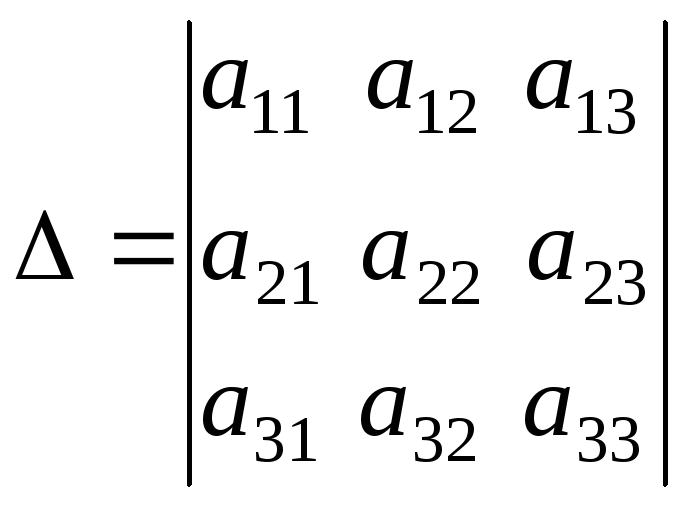, тогда .

Алгебраическое дополнение– это определитель более низкого порядка, получаемый путем вычеркивания соответствующей строки и столбца и учитывающий знак , где– номер строки,– номер столбца.

Например,

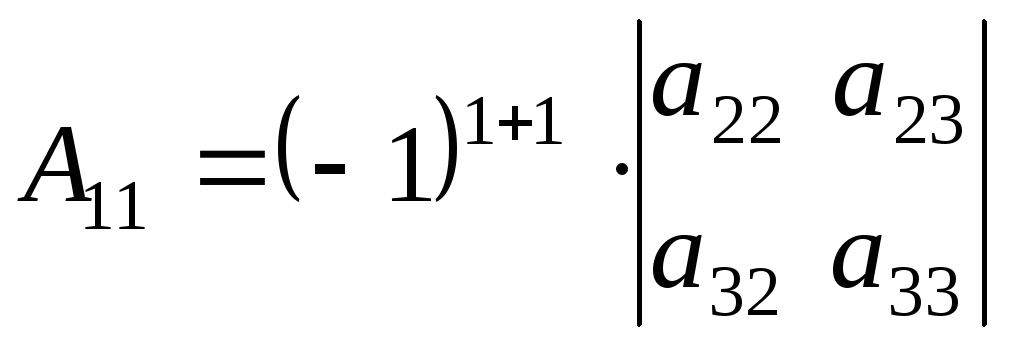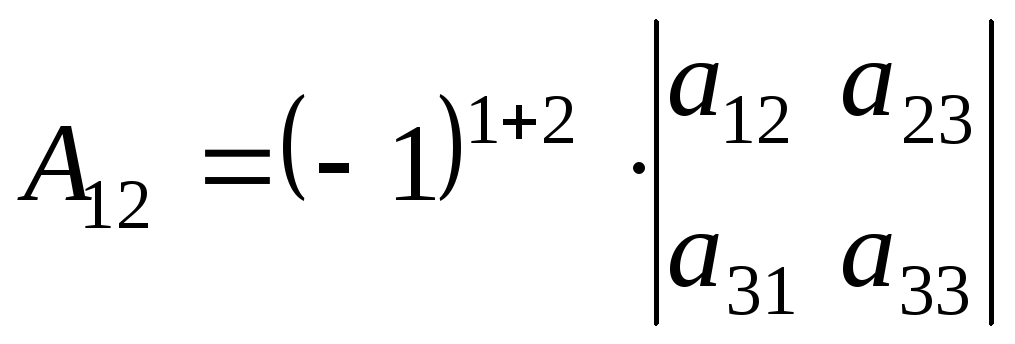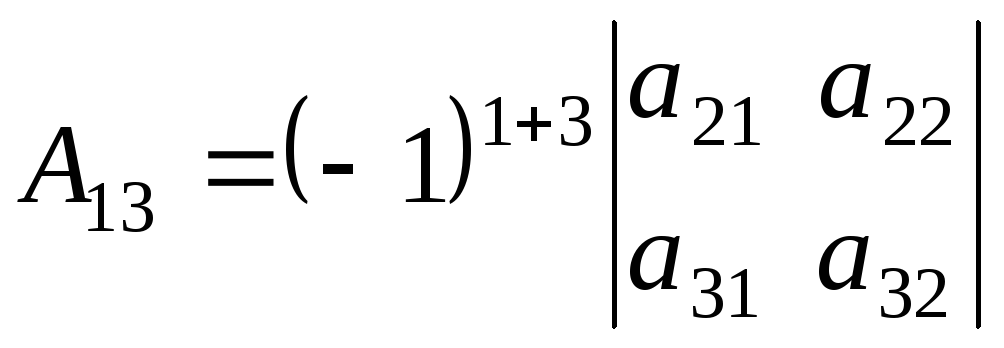, , и т.д.

Вычислим по этому правилу вспомогательные определители и , раскрывая их по элементам первой строки.

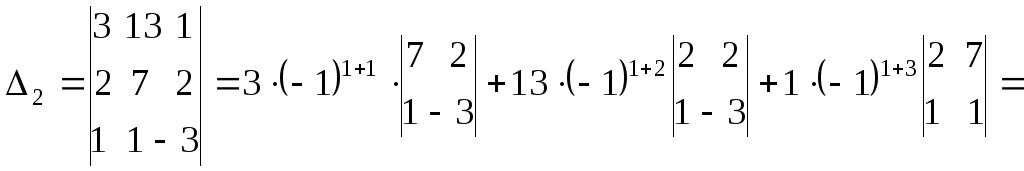
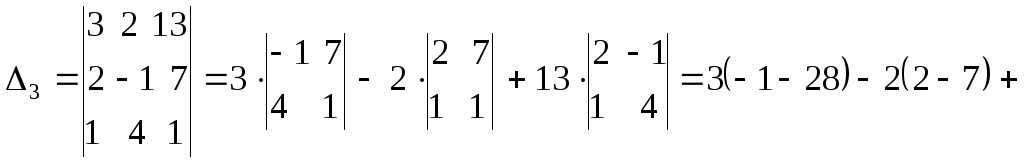
Вычислив все определители, по правилу Крамера найдем переменные:

Проверка:

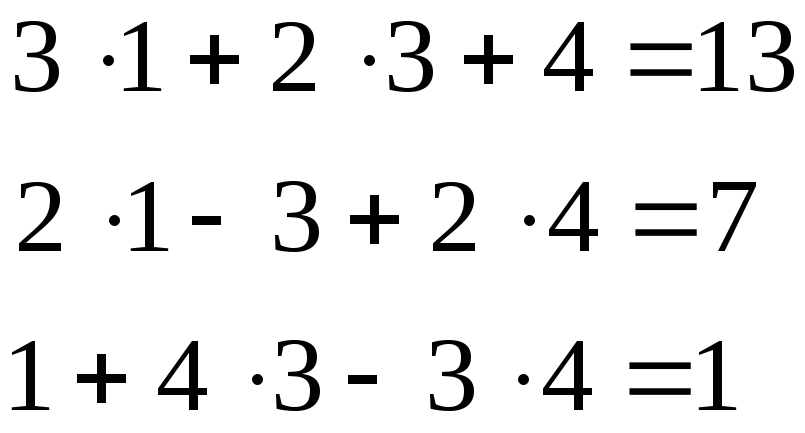
Вывод: система решена верно: .

3. Основные свойства определителей

Необходимо помнить, что определитель – это число, найденное по некоторым правилам. Его вычисление может быть упрощено, если пользоваться основными свойствами, справедливыми для определителей любого порядка.

Свойство 1.Значение определителя не изменится от замены всех его строк соответствующими по номеру столбцами и наоборот.

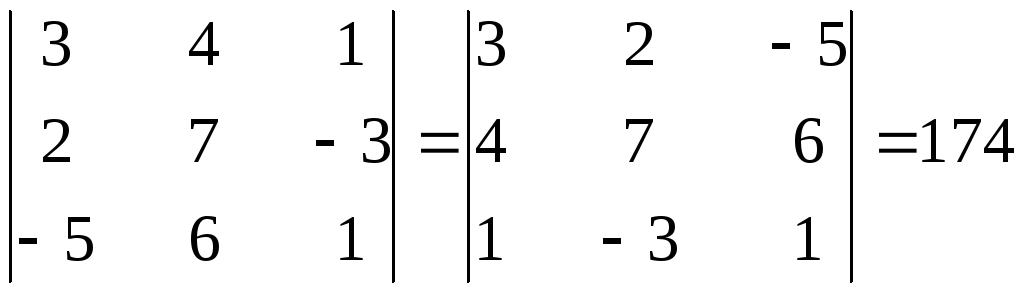
Операция замены строк столбцами называется транспонированием. Из этого свойства вытекает, что всякое утверждение, справедливое для строк определителя, будет справедливым и для его столбцов.

Свойство 2.Если в определителе поменять местами две строки (столбца), то знак определителя поменяется на противоположный.

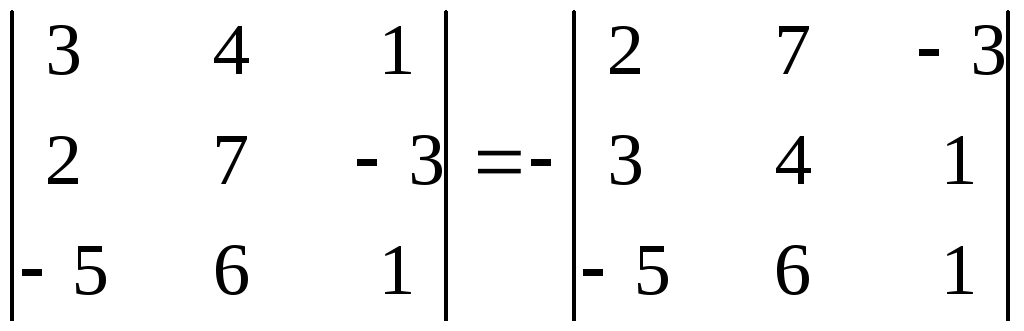
Свойство 3.Если все элементы какой-нибудь строки определителя равны 0, то определитель равен 0.

Свойство 4.Если элементы строки определителя умножить (разделить) на какое-нибудь число , то и значение определителя увеличится (уменьшится) в раз.

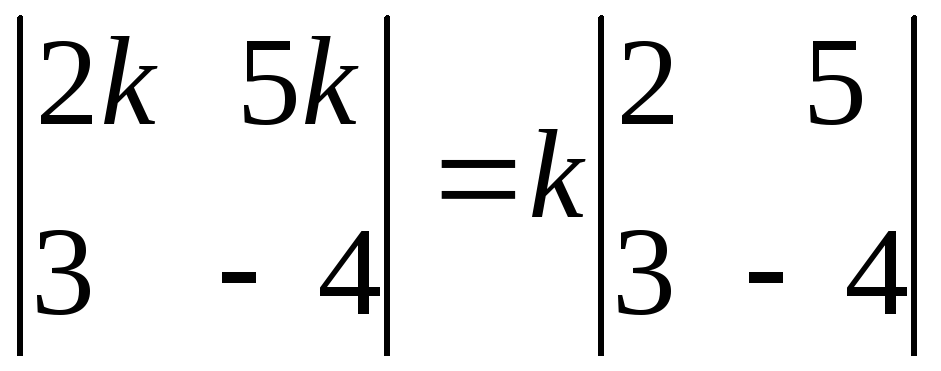
Если элементы какой-нибудь строки, имеют общий множитель, то его можно вынести за знак определителя.

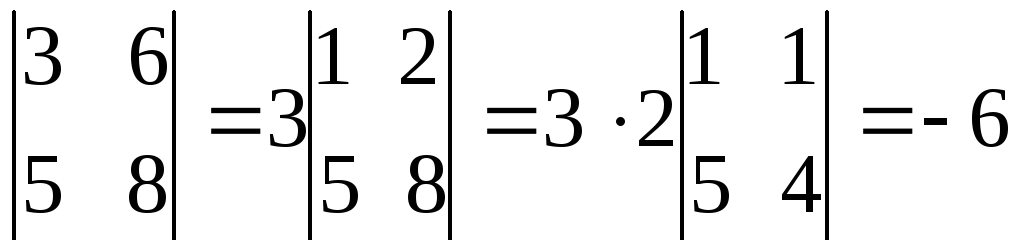
Свойство 5. Если определитель имеет две одинаковые или пропорциональные строки, то такой определитель равен 0.

Свойство 6. Если элементы какой-нибудь строки определителя представляют собой сумму двух слагаемых, то определитель равен сумме двух определителей.

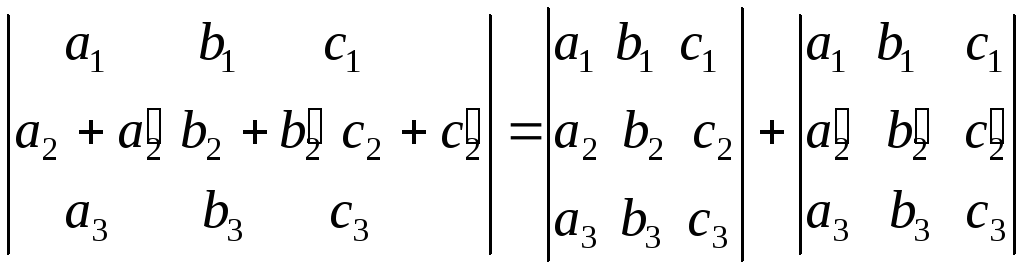
Свойство 7. Значение определителя не изменится, если к элементам какой-нибудь строки добавить элементы другой строки, умноженной на одно и то же число.

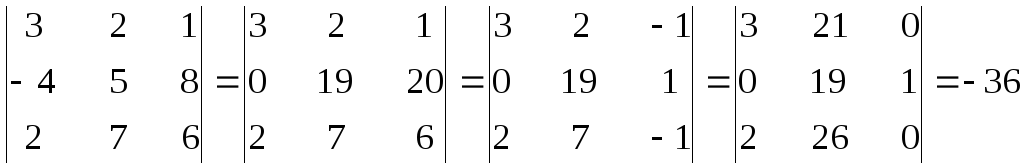
В этом определителе вначале ко второй строке прибавили третью, умноженную на 2, затем из третьего столбца вычли второй, после чего вторую строку прибавили к первой и третьей, в результате получили много нулей и упростили подсчет.

Элементарными преобразованиями определителя называются упрощения его благодаря использованию указанных свойств.

Пример 1.Вычислить определитель

Непосредственный подсчет по одному из рассмотренных выше правил приводит к громоздким вычислениям. Поэтому целесообразно воспользоваться свойствами:

а) из І строки вычтем вторую, умноженную на 2;

б) из ІІ строки вычтем третью, умноженную на 3.

В результате получаем:

Разложим этот определитель по элементам первого столбца, содержащего лишь один ненулевой элемент.

.

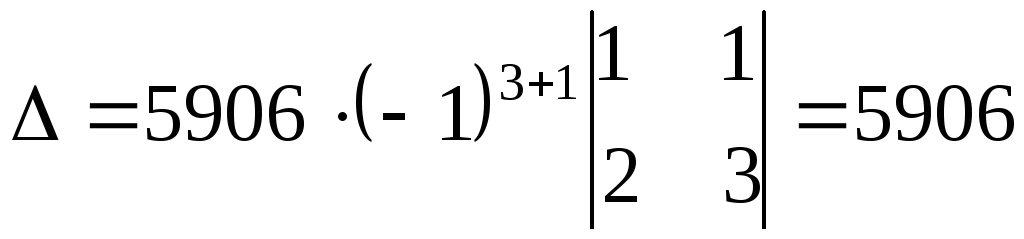3. Системы и определители высших порядков

Систему линейных уравнений с неизвестными можно записать в таком виде:

Для этого случая также можно составить главный и вспомогательные определители, а неизвестные определять по правилу Крамера. Проблема состоит в том, что определители более высокого порядка могут быть вычислены только путем понижения порядка и сведения их к определителям третьего порядка. Это может быть осуществлено способом прямого разложения по элементам строк или столбцов, а также с помощью предварительных элементарных преобразований и дальнейшего разложения.

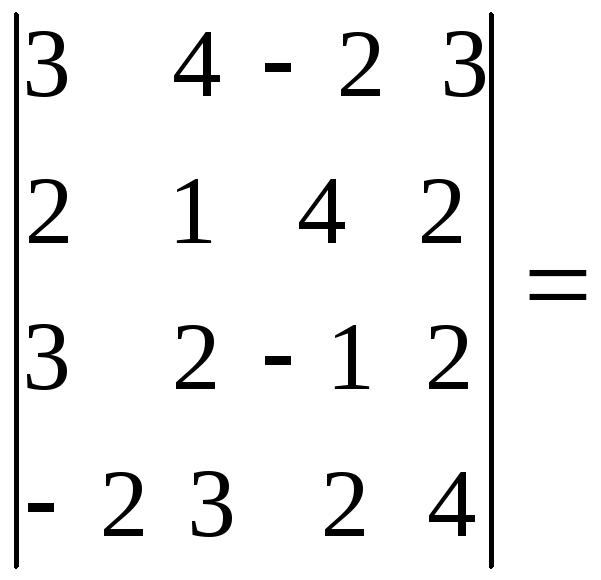
Пример 4. Вычислить определитель четвертого порядка

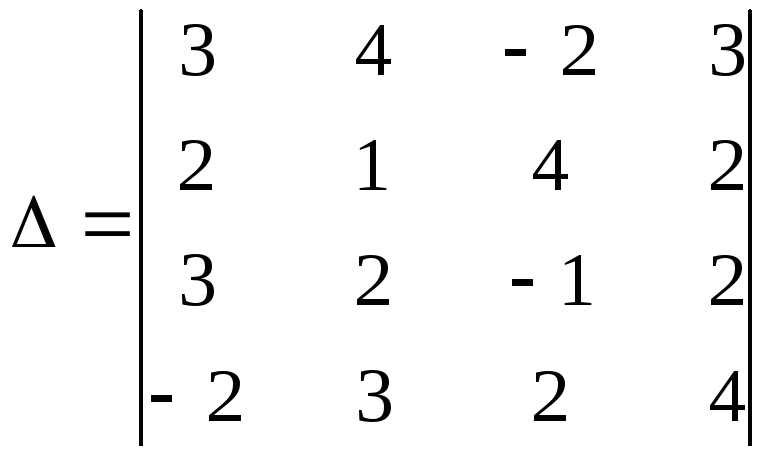
Решение найдем двумя способами:

а) путем прямого разложения по элементам первой строки:

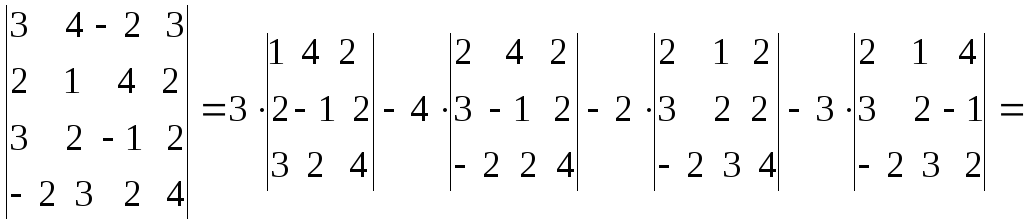
б) путем предварительных преобразований и дальнейшего разложения

	а) из І строки вычтем ІІІ
	б) ІІ строку прибавим к ІV

а) из IV строки вынесем 2
б) сложим III и IV столбцы
в) умножим на 2 III столбец и прибавим ко II

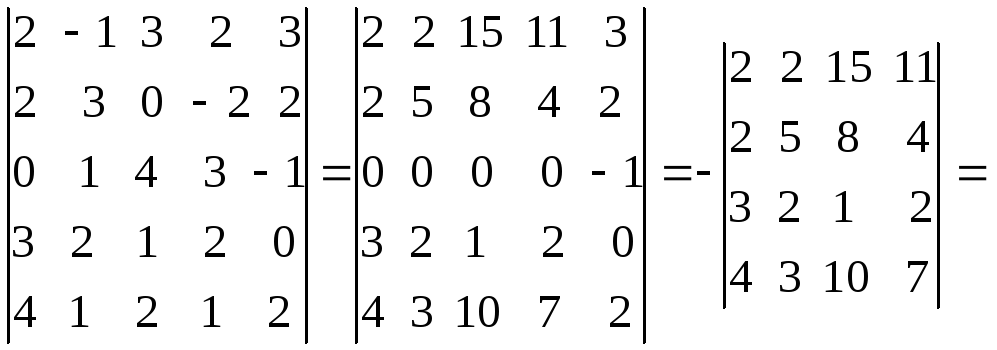
Пример 5.Вычислить определитель пятого порядка, получая нули в третьей строке с помощью четвертого столбца

из первой строки вычтем вторую, из третьей вычтем вторую, из четвертой вычтем вторую, умноженную на 2.

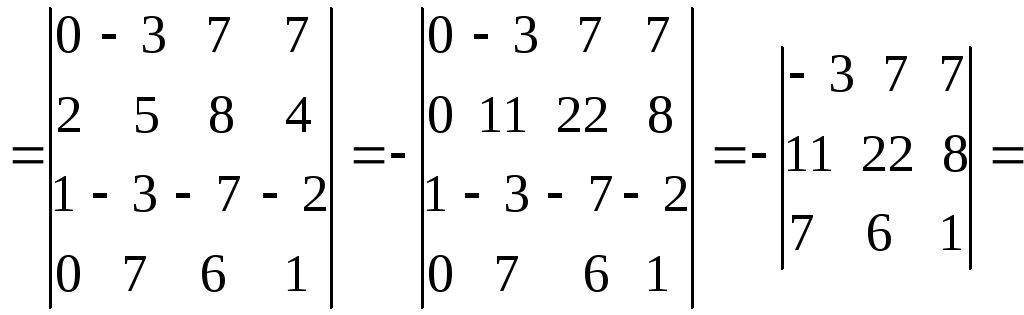
из второго столбца вычтем третий:

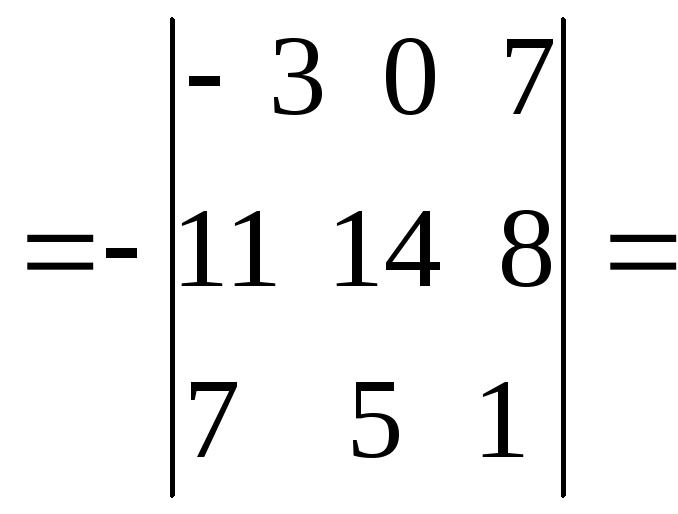
из второй строки вычтем третью:

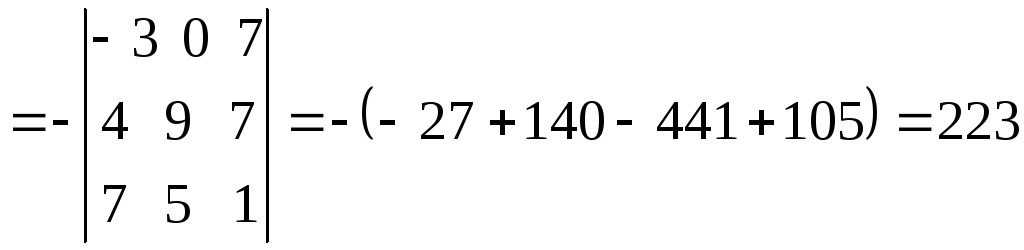
Пример 6.Решить систему:

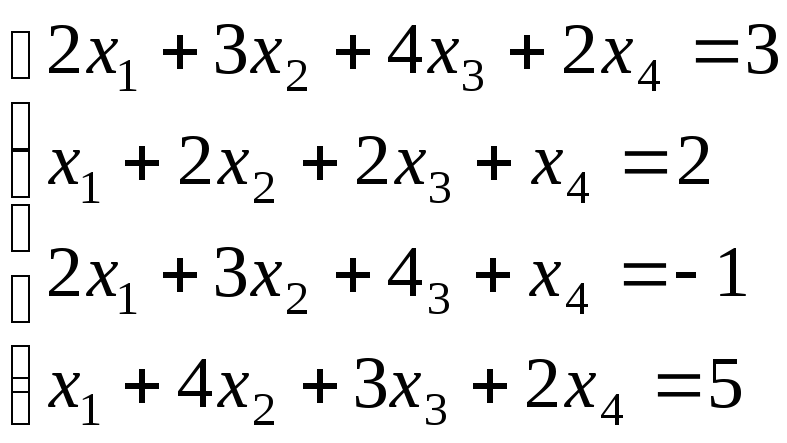
Решение.Составим определитель системы и, применив свойства определителей, вычислим его:

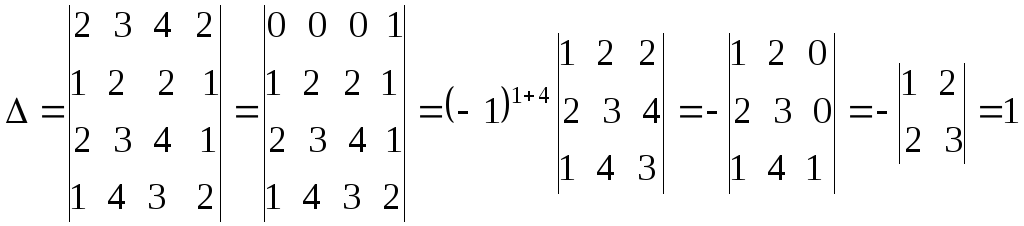
(из первой строки вычтем третью, а затем в полученном определителе третьего порядка из третьего столбца вычитаем первый, умноженный на 2). Определитель , следовательно, формулы Крамера применимы.

Вычислим остальные определители:

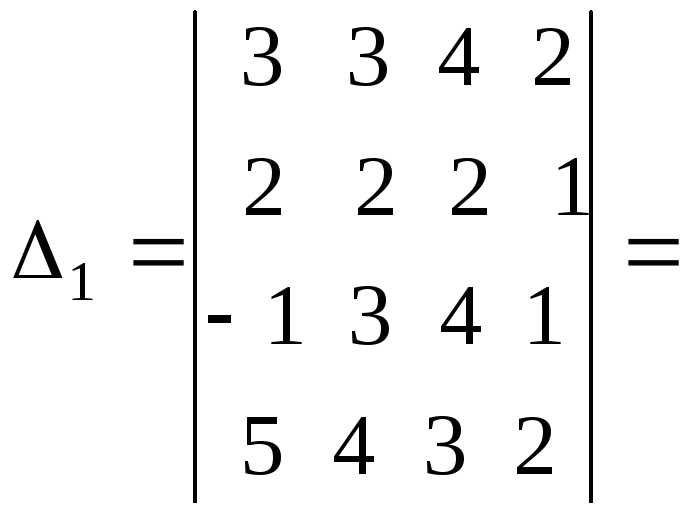
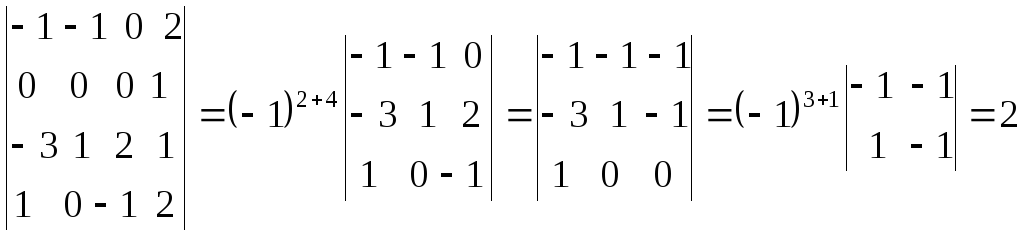
Четвертый столбец умножили на 2 и вычли из остальных

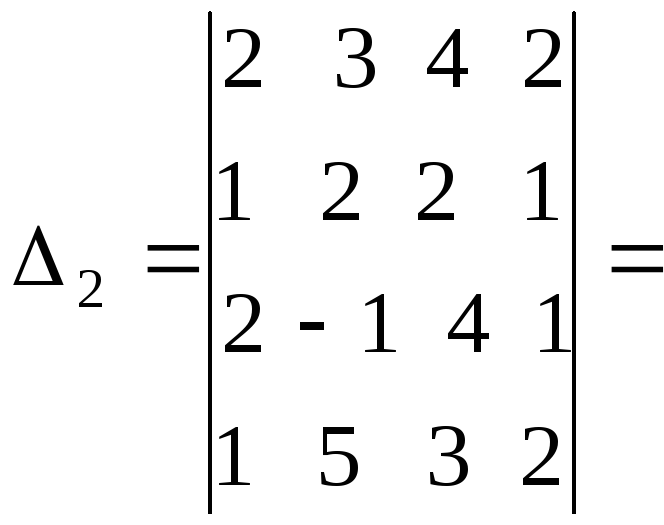
Четвертый столбец вычли из первого, а затем, умножив на 2, вычли из второго и третьего столбцов.

.

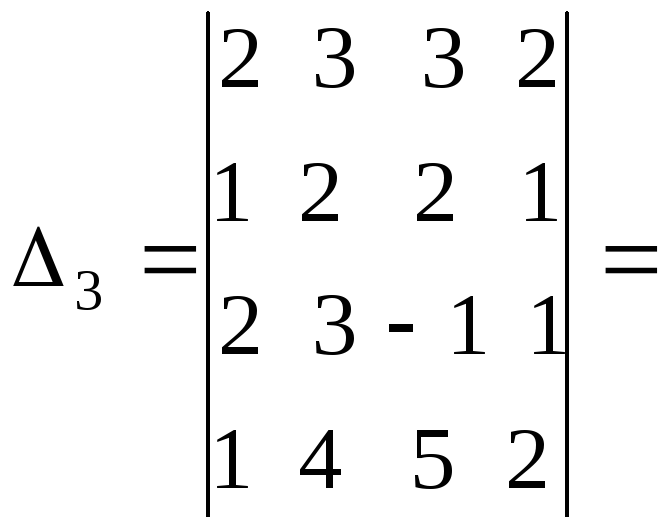
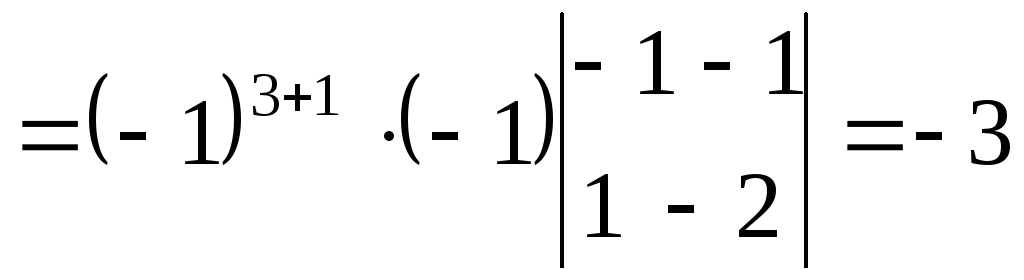Здесь выполнили те же преобразования, что и для .

.

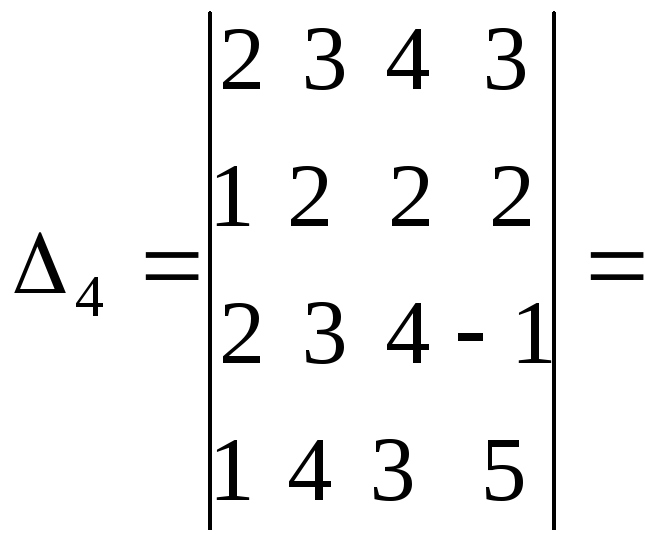
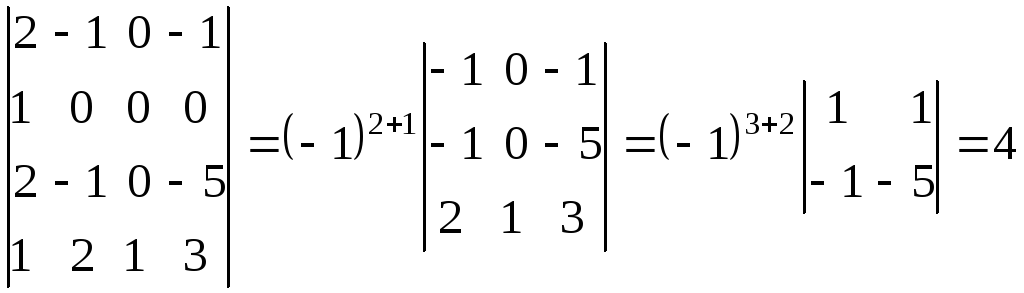При нахождении первый столбец умножили на 2 и вычли из остальных.

По правилу Крамера имеем:

.

После подстановки в уравнения найденных значений убеждаемся в правильности решения системы.

2. МАТРИЦЫ и ИХ ИСПОЛЬЗОВАНИЕ

В РЕШЕНИИ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ